时间序列
时间序列和时间序列分式分别是什么?时间序列是指将某种现象某一个统计指标在不同时间上的各个数值,按时间先后顺序排列而形成的序列。而时间序列分析 (Time series analysis) 是一种动态数据处理的统计方法。该方法基于随机过程理论和数理统计学方法,研究随机数据序列所遵从的统计规律,以用于解决实际问题。(引自百度百科)
从上述说明可以看出,时间序列不仅仅只是一个序列数据,而是一个受系统影响很大的序列数据,时间序列的数据本身存在于生活中的各个领域里。人们对时间序列的分析从很早以前就开始了,发展至今,在大数据环境下,采用数据挖掘的方法来表示数据内部规律也成为了分析时间序列的一种重要方向和趋势。
时间序列特征
时间序列变量有以下两大主要特征:
- 非平稳性(nonstationarity,也作不平稳性,非稳定性):即时间序列变量无法呈现出一个长期趋势并最终趋于一个常数或是一个线性函数。也就是说,时间序列在每个时间周期里可能出现两种变化,一种是受整个系统变化的影响,另一种是随机的变化。
- 波动幅度随时间变化(Time—varying Volatility):即一个时间序列变量的方差随时间的变化而变化。
正是因为这种不确定性和各自间的相关性,使得有效分析时间序列变量十分困难。举例来说,每个人在不同的时间点产生的行为都是随机行为,但即将产生的行为或多或少又会受个人过去的行为习惯所影响。假设当我们有这个人过去的全部行为数据时,首先希望通过某种方式刻画这个人过去的行为,并最终找到和这个人有类似行为习惯的人群。传统的划分方法很多,但都是通过某个行为来进行分类,将所有相关行为放在时间序列上来进行整体观察。就用户生命周期而言,国内外都有很多这个方向的研究。那么能否找到一种方法通过大量的数据来实践时间序列的聚类方法优劣性,并应用到实际项目中呢?
相关案例
时间序列在电子商务领域的研究,近几年才逐渐兴起。我们在项目中希望能够对有相似行为的人群做划分,但发现由于人的很多行为是相互关联的,并且在时间的维度中还会发生变化,可能受过去的影响,也可能不受影响,所以,这一秒和下一秒都是不可确定的,从传统方法的聚类存在局限性。但我们从长期趋势研究中发现消费的某些行为可能是固定的,比如定期的购买、季节的变换、促销活动的影响等,这些都是和时间周期有关系的,于是我们想到使用基于时间序列的聚类的方法来进行尝试,得到了一些新的效果。随着时间的变换,人的行为可能和时间进行关联后会产生不同的结果,我们最后不仅能得到这个用户局部的行为规律,也可以看到用户在整体时间周期里的行为的规律,通过观察整体和局部,便能更好进行用户画像。
时间序列的聚类
关于时间序列聚类的方法,简单总结如下:
- 传统静态数据的聚类方法有:基于划分的聚类、基于层次的聚类、基于密度的聚类、基于格网的聚类、基于模型的聚类;
- 时间序列聚类方法:大概有三种,一是基于形态特征,即形状变化,包括全局特征和局部特征;二是基于结构特征,即全局构造或内在变化机制,包括基本统计特征、时域特征和频域特征;三是基于模型特征,参数的的变化影响系统的变化,同时存在随机变化。
然而无论是分类、聚类还是关联规则挖掘,都需要解决时间序列的相似度问题,相似性搜索是时间序列数据挖掘的研究基础。由于时间序列存在各种复杂变形 (如平移、伸缩、间断等) ,且变形时间和变形程度都无法预料,传统的欧氏距离已经无法胜任。经过调研得知,目前动态时间弯曲 (DTW) 相似距离的稳定性已在国内外得到验证,于是我们打算采用 DTW 来尝试聚类分类。
欧式距离
我们定义两个时间序列长度为 N 的序列 T 和 D 的欧式距离如下:
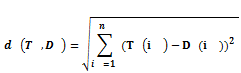
欧式距离本身也是计算空间距离的,我们刚开始选用它来计算距离,但发现单独使用准确性不高。现在,我们来做一个简单的实验:
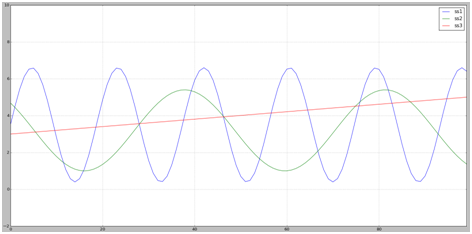
图 1 三条序列曲线
首先,用 Python 来简单的画三条曲线(如图 1),从图中可以明显的看出,ss1 和 ss2 曲线是很相似(这里就是 sin 函数的不同区间变换),ss3 和他们两个都有明显的不同。我们使用公式来计算 ss1 和 ss2,ss1 和 ss3 的距离,结果如下:
ss1 --> ss2 的欧式距离:26.959216038
ss1 --> ss3 的欧式距离:23.1892491903
从上面可以直观的发现 ss1 和 ss2 的距离值反而更大。这里只是直观的说明它本身对序列计算的问题,其实当发现时间序列的频率变化;时间扭曲的时候,单一的欧式距离公式的偏差是比较大的。
动态时间规整(Dynamic Time Warping)
动态时间规整现在应用的比较多的是在语音识别上,因为 DTW 本身是为了找到最优非线性时间序列之间的距离值。这个算法是基于动态规划(DP)的思想,解决了发音长短不一的模板匹配问题,简单来说,就是通过构建一个邻接矩阵,寻找最短路径和的犯法。现在我们继续试验,定义两个时间序列长度为 n 的序列 T 和 D。
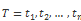
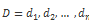
我们需要先构建一个 n x n 的矩阵,其中 i,j 是和之间的欧式距离,我们想通过这个矩阵的最小累积距离的路径。然后确定对比两个时间序列之间的距离。我们叫这个路径为 W。
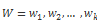
其中每个元素代表了 T 和 D 点之间的距离,例如:
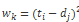
我们想找到距离最小的路径:
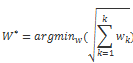
最佳路径是使用的动态规划递归函数,具体公式如下:
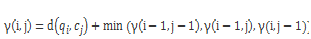
最后得到结果:
ss1 --> ss2 的 DTW 距离:17.9297184686
ss1 --> ss3 的 DTW 距离:21.5494948244
聚类
从实验后,我们最后选用了 DTW 作为时间序列的计算的方法。但在实际运行过程中,发现 DTW 的的运算速度确实比较慢,目前正在实验提升它效率的方法。有了计算方法后,我们准备开始进行聚类了。我们使用 k 近邻分类算法。根据经验,最理想的结果是当然是 k = 1 时的距离值。在该算法中,训练集和测试集分别采用的时间序列的周期集合数据集,在算法中,对测试集进行预测的每个时间序列,搜索是必须通过训练中的所有的点集,发现最相似的一点。
小结
本文只是简单介绍了在实际项目中使用时间序列聚类算法时产生的疑惑和解决思路,期间很多方法可能还是尝试和实验阶段。由于时间的原因,可能还有很多细节方面考虑不是很周到,DTW 算法比较可靠。目前我们还在通过其他一些对他的优化方法提升速度,后续会继续对电子商务用户生命周期时间序列的挖掘方法进行研究和提升,欢迎交流讨论。
作者简介:
 黄靖锋,京东算法工程师。主要负责京东用户生命周期系统架构设计与实践应用,专注于高性能大数据计算与机器学习算法的应用。
黄靖锋,京东算法工程师。主要负责京东用户生命周期系统架构设计与实践应用,专注于高性能大数据计算与机器学习算法的应用。
感谢魏星对本文的审校。
给InfoQ 中文站投稿或者参与内容翻译工作,请邮件至 editors@cn.infoq.com 。也欢迎大家通过新浪微博( @InfoQ , @丁晓昀),微信(微信号: InfoQChina )关注我们,并与我们的编辑和其他读者朋友交流(欢迎加入 InfoQ 读者交流群 (已满),InfoQ 读者交流群(#2)
(已满),InfoQ 读者交流群(#2) )。
)。












评论