系列导读:《无痛的增强学习入门》系列文章旨在为大家介绍增强学习相关的入门知识,为大家后续的深入学习打下基础。其中包括增强学习的基本思想,MDP 框架,几种基本的学习算法介绍,以及一些简单的实际案例。
作为机器学习中十分重要的一支,增强学习在这些年取得了十分令人惊喜的成绩,这也使得越来越多的人加入到学习增强学习的队伍当中。增强学习的知识和内容与经典监督学习、非监督学习相比并不容易,而且可解释的小例子比较少,本系列将向各位读者简单介绍其中的基本知识,并以一个小例子贯穿其中。
在第一篇中,我们以蛇棋为例,主要介绍了增强学习的核心流程,那就是 Agent 与 Environment 的交互。
在第二篇中,我们曾简单介绍了计算最优策略的方法——先得到同一状态下不同行动的价值估计,再根据这些价值估计计算出最优的策略选择。
本节将详细介绍采用这个战术实现的算法——策略迭代法(Policy Iteration)。
3 策略迭代法
3.1 策略迭代法
在上面的计算思路中,我们要想知道最优的策略,就需要能够准确估计价值函数。然而如果想准确估计价值函数,又需要策略是最优,数字才能够估计准确。所以实际上这是一个鸡生蛋,蛋生鸡的问题。碰上这样无解的问题,我们往往需要一些“曲线救国”的问题。我们能不能把这个问题考虑成一个迭代优化的问题,通过一轮一轮的计算逐渐接近最优的结果呢?答案是可以的。
我们的假想思路是这样的:首先以某种策略开始,计算当前策略下的价值函数;然后利用这个价值函数,找到更好的策略;接下来再用这个策略继续前行,更新价值函数……这样经过若干轮的计算,如果一切顺利,我们的策略会收敛到最优的策略,问题也就得到了解答。下面我们先来实践一下这个思路。
为了实践这个思路并验证我们的结果,我们需要将蛇棋的难度降低。我们这里将梯子数量变为 0,同时只需用两种骰子:可以投掷 1-3 的投掷手法和可以投掷 1-6 的投掷手法。对于这样的问题,我们可以直接猜测出最优的方案:在前进至 97,98,99 前,全部使用 1-6 的骰子显然可以获得最优的前进步数,而这三个位置最好使用 1-3 的骰子,因为这样有更大的概率一次性到达终点。
下面就来构建这种策略,并用两种相对简单的策略进行一下对比。两种简单的策略自然是一直使用其中的一种投掷手法不做变化。我们使用每一种策略随机进行 1 万局游戏,以下是对应的代码:
def simple_eval():
env = Snake(0, [3,6])
agent = TableAgent(env.state_transition_table(), env.reward_table())
print 'return3={}'.format(eval(env,agent))
agent.policy[:]=1
print 'return6={}'.format(eval(env,agent))
agent.policy[97:100]=0
print 'return_ensemble={}'.format(eval(env,agent))
游戏最终的平均得分如下所示:
return3=49
return6=68
return_ensemble=70
可以看出,我们设想的策略获得了最高的平均得分,说明我们的思路确实有厉害之处。如果把寻找策略的事情交给算法呢?
我们来实现一下上面提到的优化算法的两个步骤,首先是计算当前策略的价值函数估计。我们采用了迭代的方式去求解,求解的方式就是采用了 Bellman 等式:
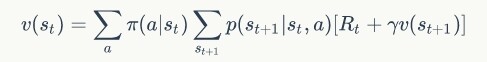
由于有的存在,每个状态的价值最终将得到收敛,于是代码可以写作:
def policy_evaluation(self):
# iterative eval
while True:
# one iteration
new_value_pi = self.value_pi.copy()
for i in range(1, self.state_num): # for each state
value_sas = []
for j in range(0, self.act_num): # for each act
value_sa = np.dot(self.table[j, i, :], self.reward + self.gamma * self.value_pi)
value_sas.append(value_sa)
new_value_pi[i] = value_sas[self.policy[i]]
diff = np.sqrt(np.sum(np.power(self.value_pi - new_value_pi, 2)))
if diff < 1e-6:
break
else:
self.value_pi = new_value_pi
完成了这一步,下一步就是根据前面的状态价值函数计算状态 - 行动价值函数:
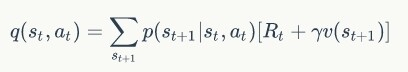
完成计算后根据同一状态下的行动价值更新策略:
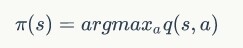
这样就完成了状态的更新。代码如下所示:
def policy_improvement(self):
new_policy = np.zeros_like(self.policy)
for i in range(1, self.state_num):
for j in range(0, self.act_num):
self.value_q[i,j] = np.dot(self.table[j,i,:], self.reward + self.gamma * self.value_pi)
# update policy
max_act = np.argmax(self.value_q[i,:])
new_policy[i] = max_act
if np.all(np.equal(new_policy, self.policy)):
return False
else:
self.policy = new_policy
return True
串联起来,整个算法的执行如下所示:
def policy_iteration(self):
iteration = 0
while True:
iteration += 1
self.policy_evaluation()
ret = self.policy_improvement()
if not ret:
break
print 'Iter {} rounds converge'.format(iteration)
那么最终执行的结果如何呢?
def policy_iteration_demo():
env = Snake(0, [3,6])
agent = TableAgent(env.state_transition_table(), env.reward_table())
agent.policy_iteration()
print 'return_pi={}'.format(eval(env,agent))
print agent.policy
结果为:
Iter 2 rounds converge
return_pi=70
[0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0]
可以看出,它求出的策略结果和我们想象中的结果是一样的,说明这种算法在这个 case 上是没有问题的。这个算法就被称为策略迭代法。可以看出,每一轮迭代后,策略进行了一次更新,当策略无法更新时,迭代结束。算法的两个部分也分别被称为:策略评估部分和策略提升部分。

3.2 策略提升的证明

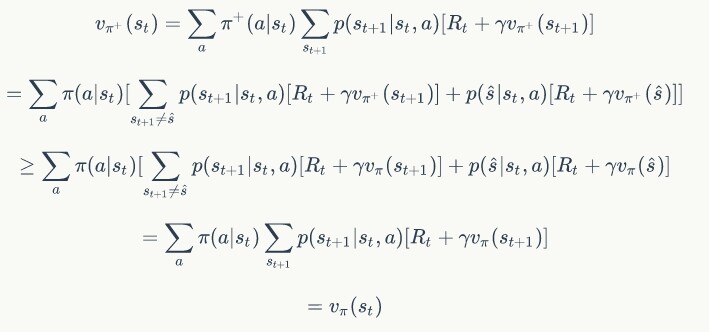
那么我们就可以对这部分策略进行更新,得到一个新的策略,这个策略除了在状态 s 的决策与原策略不同,其他完全一致,那么对于任意一个状态 s 来说,有:
所以可以证明每一次策略提升都不会对当前策略的价值造成下降,同理可以证明如果策略下状态的价值不高于策略下状态的价值,且下状态的价值又不高于,那么下状态的价值也不高于,基于这种传递性,也可以得到策略迭代不断趋近最优的性质。
3.3 策略迭代的展示
上面证明了策略迭代的分布性质,下面就来看看上面那个例子中分布迭代的具体表现。我们假设一开始所有的策略都采用 1-3 的投掷手法,于是在第一轮策略评估中,我们共进行了 94 轮迭代,过程中的状态的迭代值在不断变化,我们以”50“这个位置为例,做一张 94 轮迭代下价值的变化值:
图 1 第一轮策略评估时位置“50”的价值变化图
其中横轴为迭代轮数,纵轴为价值,可以看出随着迭代轮数的增加,价值总体趋于平稳。完成第一轮的策略提升后,实际上策略已经被更新为最优策略,于是在第二轮策略评估中,再经过 94 轮迭代,”50“位置的价值又经历了如下的变化:
图 2 第二轮策略评估时位置“50”的价值变化图
看完了上面那个简单的例子,下面让我们回到复杂的例子中来,对于一个拥有 10 个梯子的问题,策略迭代会给我们如何的解答呢?
def policy_iteration_demo():
env = Snake(10, [3,6])
agent = TableAgent(env.state_transition_table(), env.reward_table())
print 'return3={}'.format(eval(env,agent))
agent.policy[:]=1
print 'return6={}'.format(eval(env,agent))
agent.policy[97:100]=0
print 'return_ensemble={}'.format(eval(env,agent))
agent.policy_iteration()
print 'return_pi={}'.format(eval(env,agent))
print agent.policy
结果如下:
return3=-45
return6=21
return_ensemble=31
return_pi=41
[0 1 0 0 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 0 1 1 1 1 1
1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 0 0]
可以看出,策略迭代的方法优于前面的三种方法,经过 4 轮迭代,它的策略已经将两种手法混合使用了。我们可以猜想,它一定是在靠近上升梯子附近使用 1-3 的投掷手法,在靠近下降梯子或者无梯子时使用 1-6 的投掷手法,对于最后几步自然是使用 1-3 的投掷手法。所以从最终的策略,我们也可以猜出棋盘的样子。
以上就是策略迭代的算法,除了这种算法之外,我们还有一些其他的方法,下一节我们就来介绍其他方法。
作者介绍
冯超,毕业于中国科学院大学,猿辅导研究团队视觉研究负责人,小猿搜题拍照搜题负责人之一。2017 年独立撰写《深度学习轻松学:核心算法与视觉实践》一书,以轻松幽默的语言深入详细地介绍了深度学习的基本结构,模型优化和参数设置细节,视觉领域应用等内容。自 2016 年起在知乎开设了自己的专栏:《无痛的机器学习》,发表机器学习与深度学习相关文章,收到了不错的反响,并被多家媒体转载。曾多次参与社区技术分享活动。




