在上一篇《基于交易的记账系统》中,我们从一个全新的视角重新审视了现金 —— 就法币来说,人们并不拥有法币,而是拥有“支配法币的权利”,这项权利是由各国政府赋予每一个公民的合法权益。尽管听上去仅仅是换了一种说法,但是这样的视角切换会让我们更好地理解比特币的本质。
在比特币系统中,“赋予”人们支配权力的不再是任何一个国家或权威机构,而是每个人手中攥着的私钥和公钥。私钥与公钥的关系,就像是一个人的 DNA 与指纹的关系,独一无二的 DNA 经过一系列精密的生物算法生成并世无两的指纹。那么,更技术一点,公私钥究竟是什么?非对称加密又是什么古老的黑魔法?本篇咱们就来探讨比特币幕后的 Rule maker(制定规则的主宰):非对称加密算法。
DNA 与指纹的类比
对于绝大多数人来说,加密并不陌生,生活中随处可见,如文档加密、磁盘加密、网络传输加密等等。不过,“加密”前面带个“非对称”,这就让人丈二和尚 —— 摸不着头脑了。没有比较就没有鉴别,鉴于“非对称”这个字眼儿天生的神秘感,咱们不妨先来回顾一下对称加密。所谓对称加密,如计算机网络中常用的 DES 算法、RC 算法系列,指的是加密与解密这两个成对的操作使用的是同一把秘钥 —— 因此称作对称加密。这很符合常识,生活中家里的防盗门,我们都是用同一把钥匙上锁/解锁。对称加密的优点是算法的计算量小、速度快、效率高;缺点也很明显,列位想象一下,如果不小心把家里防盗门的钥匙弄丢了,就问你心里慌不慌?因此,一直以来对称加密的安全性饱受质疑,非对称加密正是在这样的背景下诞生的。
与对称加密不同,非对称加密算法提供两把秘钥,一把称为私钥(Private Key),另一把称为公钥(Public Key)。私钥需要妥善保管,不可以泄露给任何人,而公钥则可以分发给任何想要和你通信的人。非对称加密算法根据一组随机数创建私钥,再根据私钥生成公钥。需要注意的是,这两个创建过程都是单向、不可逆的,即没有办法从公钥反推私钥、也不能根据私钥反算最开始的随机数。非对称加密算法保证私钥与公钥之间具有这样的特性:
公钥加密的信息,只能通过私钥来解密,公钥不能解密自己加密的信息
同理,私钥加密的信息,也只能通过公钥来解密,私钥也无法解密自己加密的信息
简言之,两把钥匙,加密用其中一把,而解密则只能用另一把,算法的这种特性也解释了非对称这个称呼的由来。二战时期纳粹德国采用 Enigma 作为传递军事情报的密码机,Enigma 通过转动圆盘和电路创造出前所未有的高强度密码。在那个时候,很多人都认为 Enigma 是一种无法破译的密码机,直到现代计算机之父阿兰图灵(Alan Turing)将其攻破从而扭转二战战局。本质上,Enigma 是一种对称加密算法,如果当时纳粹德国采用非对称加密技术来传递军事情报,那么二战的历史进程真的是不堪设想。

私钥上锁、公钥解锁

公钥上锁、私钥解锁
言归正传,到目前为止,非对称算法家族也非常庞大,常见的有 RSA 算法、ECC 椭圆曲线算法等等,比特币系统的实现中正是采用了椭圆曲线算法来创建成对的私钥与公钥。要说清楚这种反人类直觉的算法(如椭圆曲线算法系列)的工作原理自然是没那么容易 —— 至少生活中还没遇到过必需配备两把不同钥匙的门锁,咱们不如先从使用的角度来看看非对称加密算法常见的一些应用场景。非对称加密的使用场景有二:
加解密
数字签名与身份验证
在加解密的用途中,操作流程是公钥加密、私钥解密,主要用于保障消息在网络中的安全传输;第二个唤作数字签名与身份验证,操作流程恰好相反:私钥加密、公钥解密,这种用法的主要意图不再是消息本身的加解密,而是为了验明正身。
加解密
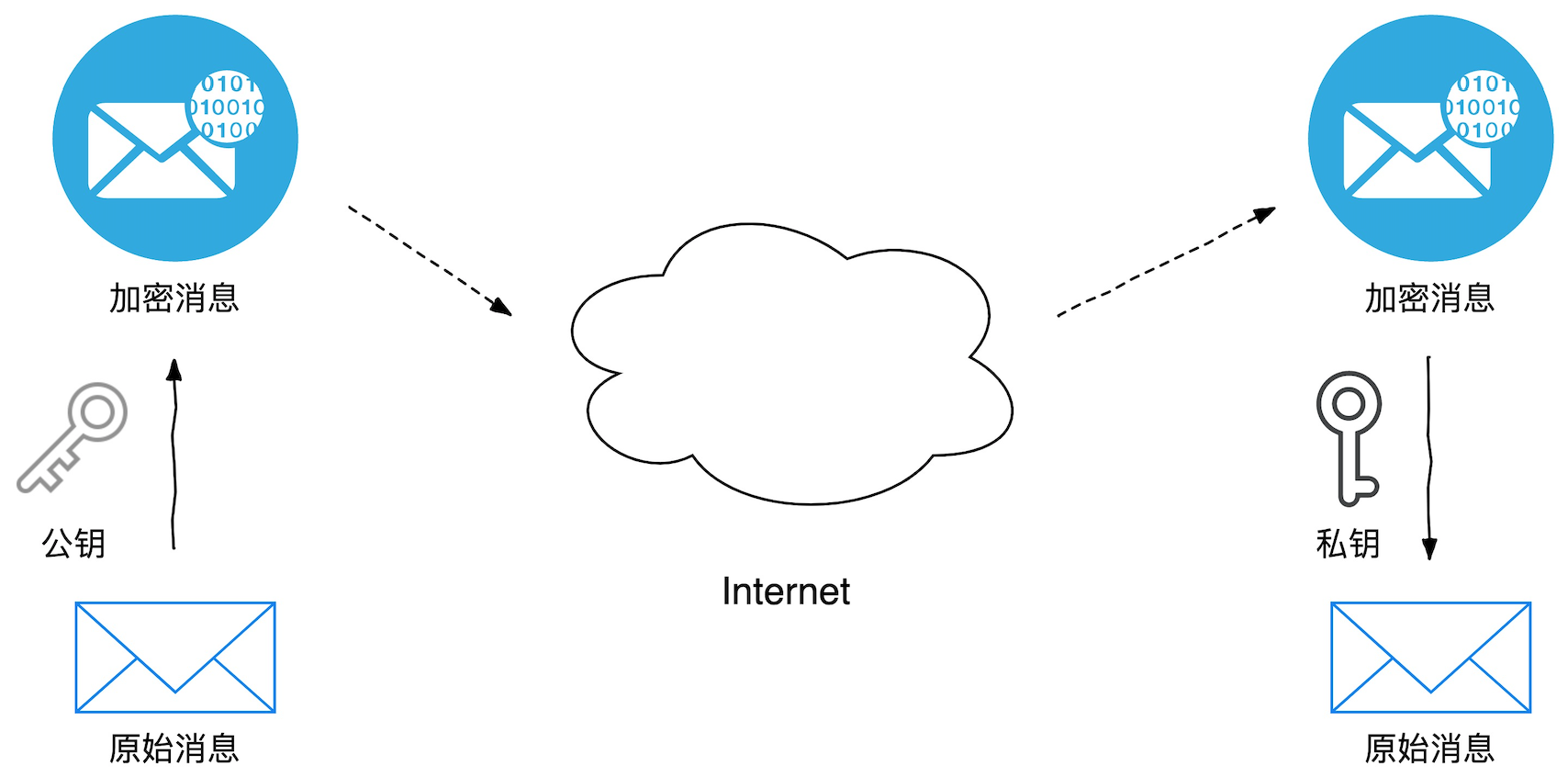
公钥加密-私钥解密
举个例子,笔者用 ECC 算法生成了一副秘钥对(私钥与公钥),自己保管私钥,把公钥分发给了好友李雷和韩梅梅。他们俩拿到公钥后,即可向我发送用公钥加密后的密文信息,由于公钥加密的消息只能用对应的私钥解密,因此我不用担心他们发送的消息在经过网络传输的过程中被拦截、窃听,窃听者即便截获到密文也是徒劳,毕竟他手中没有私钥,得到的密文对他来说仅仅是一堆无法辨识的乱码。李雷和韩梅梅即便是将消息密文广播到全网,整个网络中也只有笔者可以成功读取密文中的消息,这个过程便是典型的非对称加密技术加解密的应用场景。
数字签名与身份验证
再来说说数字签名与身份验证,这里咱们先来区分两个过程相似但是截然不同的概念:密文与摘要。密文(Cipher text)指的是明文消息被加密后的无损字节序列,无论是采用对称算法还是非对称算法进行加密,技术上密文终归可以被解密从而得到原始的明文消息。摘要(Hash digest)则不同,它指的是明文消息经过哈希运算(Hash algorithm)得到的有损字节序列,之所有说是“有损”,原因在于哈希运算过程不可逆,换句话说,在技术上无法通过某种运算过程从摘要反推原始的明文消息。考虑到哈希运算在比特币系统实现中的广泛应用(如比特币地址、比特币挖矿、比特币区块链等等),咱们不妨搂草打兔子、见缝插针 —— 穿插着说几嘴哈希算法。
首先,哈希算法是统称、是一类算法,生活中比较常见的是 MD5,网络上大型文件的下载通常都会附带 MD5 摘要用于帮助用户确认下载文件的一致性,比特币系统中应用比较广泛的是 SHA256 和 RIPEMD160。
哈希运算最重要的特性是单向、不可逆,这个特性就好比是三维空间到二维空间的映射。将任何一个三维几何体投影到二维空间,都可以得到它在二维空间的投影;反过来,从二维空间的视角出发,对于任意一个二维空间投影,我们是无论如何也无法判断它的本体在三维空间中到底生得什么模样。原因很简单 —— 从三维到二维的映射过程丢失了整整一个维度的信息,也即这个映射运算是有损的。哈希运算的不可逆特性,大抵如此。
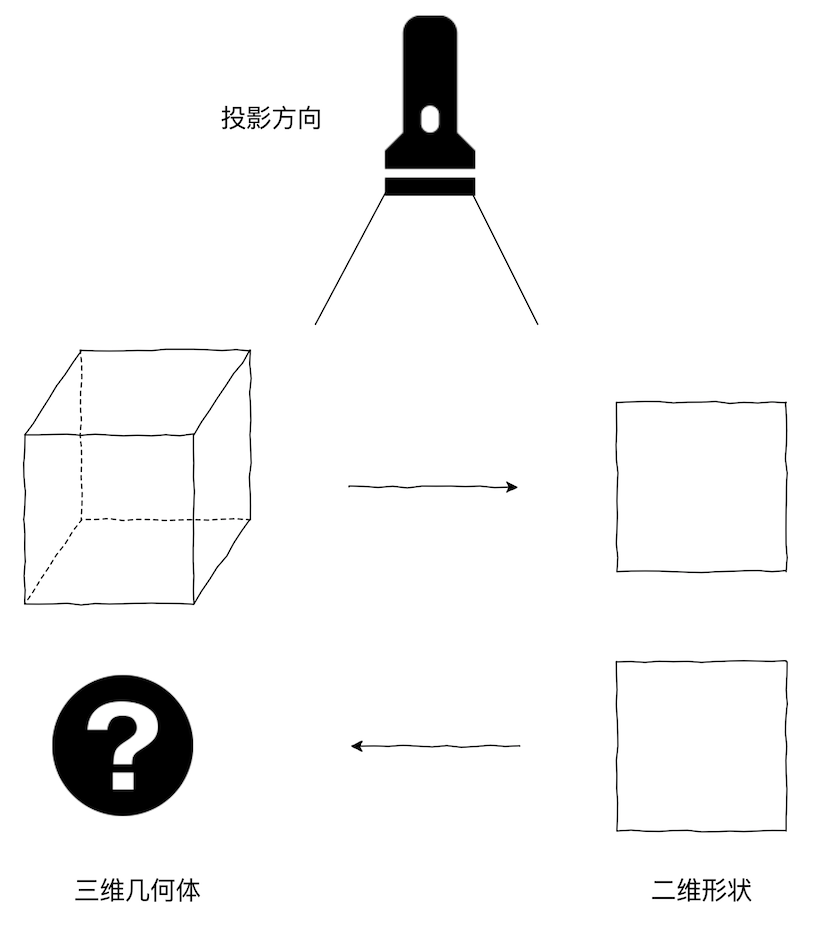
三维到二维的投影
再说回身份验证,前面咱们提到身份验证的流程是私钥加密、公钥解密,我们先来直观地感受一下这个过程。
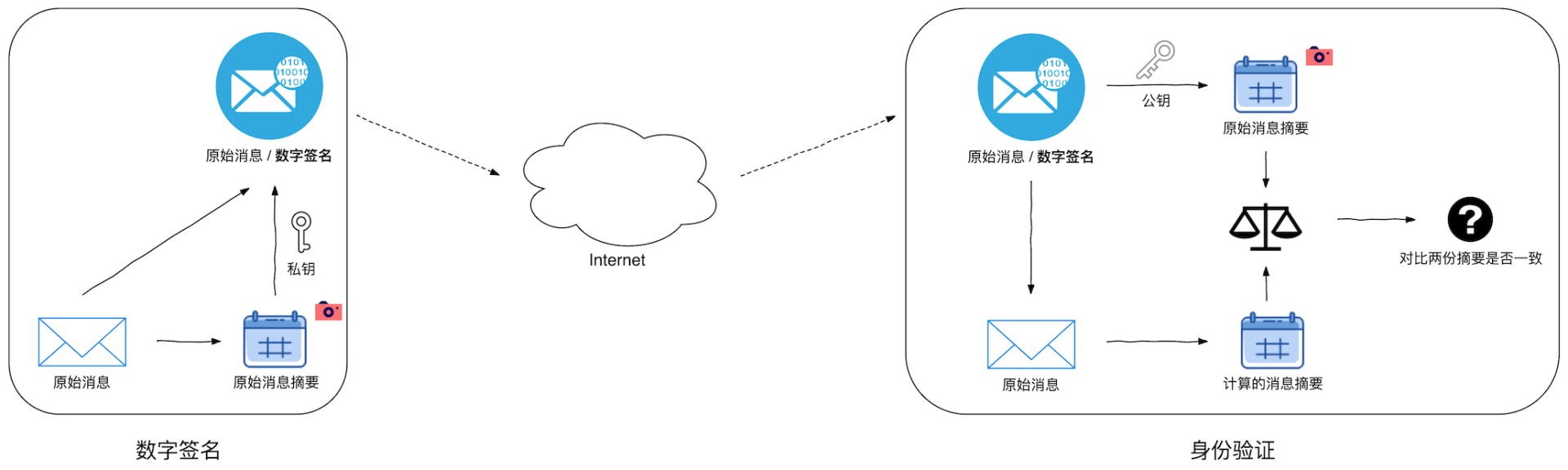
数字签名与身份验证
还是沿用刚刚的例子 —— 笔者保管私钥,李雷和韩梅梅持有对应的公钥。首先,对原始的明文消息进行哈希运算得到消息摘要,紧接着用私钥对这个摘要进行加密,加密之后的得到的密文就是所谓的“数字签名”,最后,笔者同时把明文消息和数字签名广播到网络中。在接收端,李雷或韩梅梅在接收到广播的明文和数字签名后,首先用公钥对数字签名进行解密从而获得原始的消息摘要,然后用同样的哈希算法对接收到的明文消息再次计算其摘要,最后比对两个摘要(接收到的摘要和计算得到的摘要)是否一致,从而验证发送方的身份。
所谓身份验证,具体到我们的例子中,指的是当李雷或韩梅梅用笔者的公钥成功解密且两份摘要完全相同时,即可判定消息有效且发送方一定是笔者本人。相反,两个环节但凡有一个失败 —— 要么发送方不是笔者本人(用公钥解密数字签名失败),要么消息在传输途中已被拦截篡改(两份摘要不一致),无论是哪种情况,对于接收到的明文消息和数字签名,接收方均判定消息来源不可靠。
身份验证的内在逻辑在于:如果公钥持有者(李雷或韩梅梅)可以成功解密,那么他们接收到的消息一定是由私钥持有者(笔者)发送的 —— 否则解密必然失败,又因为接收方默认私钥持有者的身份(笔者),从而使得接收方得以验证发送者的身份。细心的读者可能会发现这里藏着个 BUG,也即身份验证其实是“认(私)钥而不认人”的,也即接收方只能确定手中持有的公钥与发送者的私钥相匹配,至于私钥的持有者到底是不是笔者本人,李雷和韩梅梅无从判定,他们无法得知笔者是否已将私钥遗失、或是被人绑架胁迫从而导致私钥流入他人之手。之所以较这个真儿,主要是想强调私钥保管的重要性,在比特币交易系统中,一旦你不小心将私钥遗忘或者遗失,那么效果等同于“烧钱”。
赋予支付的权利
要弄清楚“烧钱”是怎么回事,咱们还是得回到本篇的题眼:比特币如何利用非对称加密赋予人们支付的权利?根据上文对于数字签名与身份验证的介绍,支付 BTC 的过程无外乎是:
给定原始消息明文(由比特币交易信息构成)
对明文执行哈希计算得到摘要,用私钥对摘要加密得到数字签名
用公钥对数字签名进行身份验证

支付权利赋予 3 步走
那么,在比特币交易系统中,原始消息明文由哪些要素构成呢?咱们还是沿用上一篇《基于交易的记账系统》中示例的 3 笔交易,如下图所示。对于交易 tx-00825 和交易 tx-00901,韩梅梅如果想要花费其中的 BTC,她必须提供有效的数字签名才能达成。生成数字签名的原始消息明文由如下几部分构成:
前两笔交易的 UTXO,即 UTXO:tx-00825/0 和 UTXO:tx-00901/1
尝试行使支付权利的交易 tx-00963 中借方的公钥
原始消息明文的构建过程如下图中步骤 1 所示,之后对该明文进行哈希运算得到摘要,最后在步骤 3 中用私钥对其加密生成数字签名。
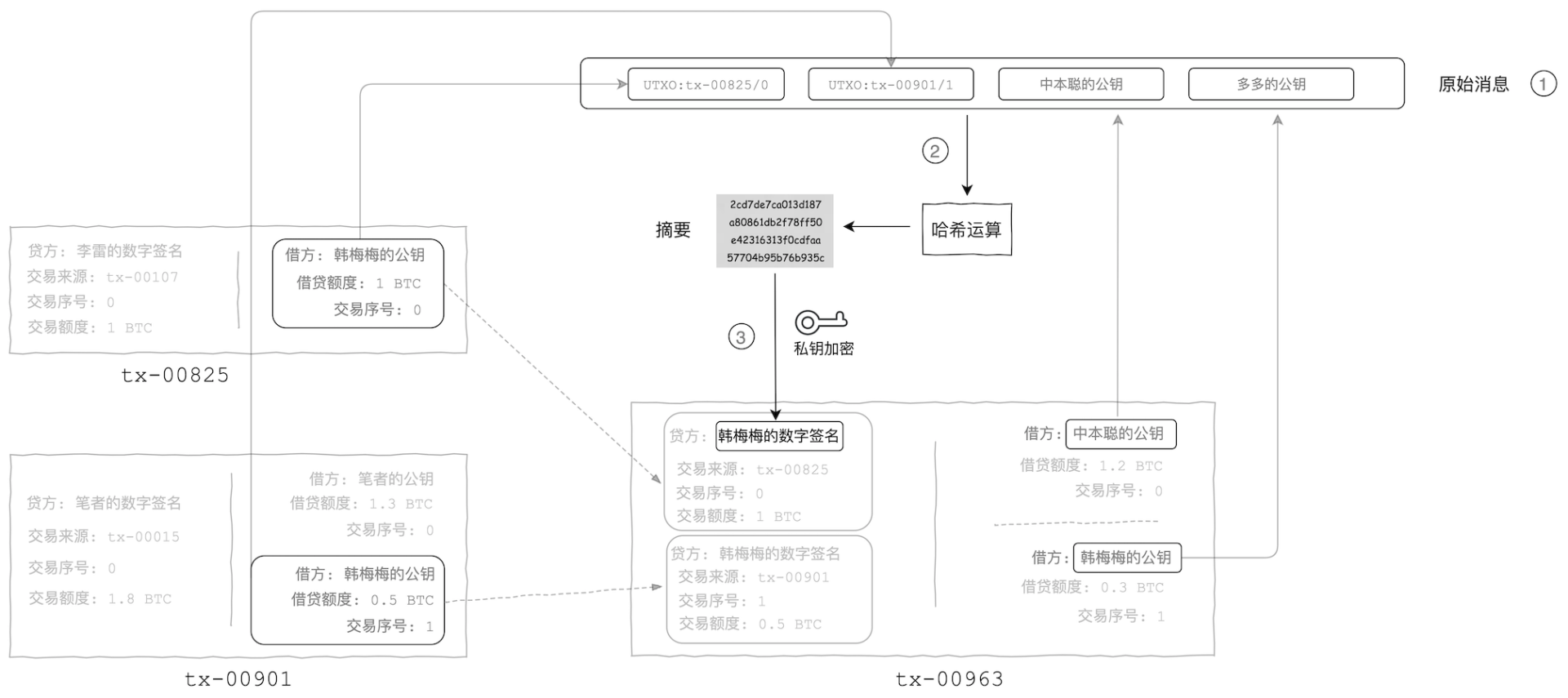
比特币交易生成数字签名的过程示意
对于交易 tx-00963 中韩梅梅的数字签名,如果存储于 UTXO:tx-00825/0 和 UTXO:tx-00901/1 中韩梅梅的公钥能够有效地对其进行身份验证,那么比特币交易系统将认定交易 tx-00963 有效,同时赋予韩梅梅支付那两笔 UTXO 中 BTC 的权利。由此可见,为了行使支付的权利,数字签名不可或缺,而数字签名又是基于私钥生成的,因此,如果私钥持有者不慎将私钥遗失、遗忘,那么所有转账给该持有者的 BTC 都将被冻结、无法流通。拿韩梅梅来举例,如果韩梅梅遗失私钥,那么她便没有办法提供数字签名从而花费属于她的 BTC,UTXO:tx-00825/0 和 UTXO:tx-00901/1 中总共 1.5 个 BTC 将永远被尘封、永无出头之日——换句话说,这 1.5 个 BTC 被凭空“烧”掉了。因此,私钥的保管尤为重要。
直观上来看,比特币中数字签名与身份验证的过程还是蛮繁琐的,在后文书中,我们会频繁地提及这个过程,为了方便大家记忆,咱们不妨臆造一个魔法咒语。在开篇时我们提到,私钥与公钥的关系,就好像是 DNA 与指纹的关系。无论是从私密性、不可逆性的角度,还是从派生过程来看,两者都及其相似。鉴于私钥与公钥、DNA 与指纹都是成对出现,我们不如捏造个“派尔伊特”(Pair it!)的魔法咒语,就如下图所示。
魔法咒语:派尔伊特 —— 类比数字签名与身份认证
“派尔伊特”的魔力在于,咒语的施法者能够以自己的 DNA 为原料召唤一个独一无二的藏宝箱,密封的宝箱内存有宝物,特殊的地方在于,只有用施法者的指纹才能再次打开这个藏宝箱,除此之外,别无他法。那么这个魔法咒语和数字签名、身份验证怎么对应呢?施法“派尔伊特”咒语而召唤的宝箱就相当于是数字签名,如果用施法者的指纹拓片(指纹拷贝)能够打开宝箱并且取出其中宝物,即可验证宝箱是由施法者召唤的、宝物是由施法者放置的——这相当于是身份验证的过程。希望这个虚构的魔法咒语能让你对于数字签名与身份验证的印象更为深刻。
Postscript
本篇是《漫话比特币》科普系列的第二篇,该科普系列面向所有具备计算机基础知识的读者,尽可能地采用生活化类比和示例来帮助读者更好地理解、消化技术内幕中涉及的关键知识点,如哈希算法、非对称加密、交易的结构、区块链的构成,等等。
为了让读者能够专注于比特币系统的整体实现,本系列隐去了一些技术细节,如哈希算法的工作流程、椭圆曲线加密的工作原理等,更多地从每一个技术点的特性、特点、用途出发,逐渐勾勒出比特币系统的全貌。笔者学浅才疏、疏漏难免,还请广大读者朋友批评、指正,更欢迎您一起参与探讨比特币、区块链的相关话题。
在本篇,我们主要探讨了比特币如何通过非对称加密技术的数字签名和身份验证来赋予支付 BTC 的权利。UTXO 中的公钥若能成功地验证交易输入中的数字签名,则说明私钥持有者是该 UTXO 中所含 BTC 的主人,具备支付权利,权利的赋予机制一目了然。不过,实现权利赋予机制的方式不止一种,在 UTXO 中直接存储公钥的方式对匿名性不够友好、或多或少存在着安全隐患,那么,还有什么更好的方式在实现权利赋予的同时能够兼顾匿名性与安全性呢?下一篇《匿名性:公钥的再加工》带你走进比特币地址——一个耳熟能详但扑朔迷离的概念,敬请期待!





