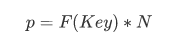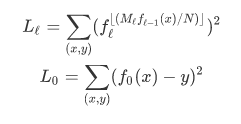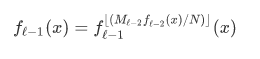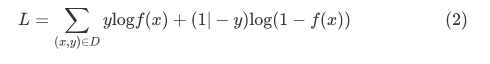Jeff Dean 在 SystemML 会议上的论文解读：学习索引结构的一些案例

学习索引结构的一些案例

The Case for Learned Index Structures
Tim Kraska1 MIT Cambridge, MA kraska@mit.edu
Alex Beutel Google, Inc. Mountain View, CA alexbeutel@google.com
Ed H. Chi Google, Inc. Mountain View, CA edchi@google.com
Jeffrey Dean Google, Inc. Mountain View, CA jeff@google.com
Neoklis Polyzotis Google, Inc. Mountain View, CA npolyzotis@google.com

译注

原文： https://www.arxiv-vanity.com/papers/1712.01208/
视频： https://www.youtube.com/watch?v=PWv4ROEvqmk

如果想下载 PDF 或者进一步讨论的可以到这里： https://gitee.com/hardysimpson/sysML

0. 摘要

索引是模型：B 树索引可以被看作是一个模型，用于将键 (Key) 映射到排序数组中的值记录 (Value) 位置，Hash 索引作为模型将键 (Key) 映射到未排序数组的值记录 (Value) 位置，BitMap 索引作为模型来指示值记录 (Value) 是否存在。 在这个探索性研究论文中，我们从这个前提开始，并假定所有现有的索引结构都可以用其他类型的模型取代，包括我们称为学习索引的深度学习模型。关键的想法是，模型可以学习查找键 (Key) 的排序顺序或结构，并使用这个信息来有效地预测值记录 (Value) 的位置或存在。 我们从理论上分析了在哪些条件下，学习索引优于传统索引结构，并描述了设计一个好的学习索引的主要挑战。 我们的初步结果表明，通过使用神经网络，学习索引能达到比高速缓存优化的 B-Tree 快 70% 的速度，并且节省几个数量级的内存，来索引几个真实世界的数据集。 更重要的是，我们相信通过深度学习模型取代数据管理系统的核心组件对于未来的系统设计有着深远的影响，而且这项工作只是提供了一些可能的一瞥。

1. 介绍

无论何时需要有效的数据访问，索引结构都是答案，并且存在各种各样的选择来满足各种访问模式的不同需求。 例如，B 树是范围查找的最佳选择（例如，在特定时间范围内检索一段值记录 (Value)）; HashMap 在单 Key 查找这个领域是无敌的 ; 而 Bloom-filter 通常用于检查值记录 (Value) 是否存在。 由于数据库和许多其他应用的索引非常重要，因此在过去的几十年里，它们已经得到了广泛的优化，以获得更高的内存、缓存和 CPU 效率 [ 28,48,22,11]。

然而，所有这些索引仍然是通用数据结构，假设数据的最坏情况分布，并没有利用现实世界数据中存在的更常见模式。 例如，如果目标是建立高度特定的系统，用来存储和查询具有连续整数键 (Key) 的固定长度值记录 (Value)（例如，键 (Key) 从 1 到 100M），那么设计者就不会使用常规的 B 树索引，因为键 (Key) 本身可以用作偏移量来作查找或者范围查询，达到 O(1) 而不是 O(long n) 的时间复杂度。 而且，索引内存大小将从 O(n) 减小到 O(1) 。也许令人惊讶的是，对于其他数据结构，相同的优化仍然是可能的。 换句话说，了解确切的数据分布可以高度优化数据库系统使用的几乎所有索引。

当然，在大多数现实世界的用例中，数据并不完全遵循已知的模式，为每个用例构建专门解决方案的代价都太高了。 然而，我们认为机器学习为挖掘数据里面的模式和相关性提供了一个机会，从而能够以低工程成本，自动合成我们称为学习索引的索引结构。

在本文中，我们探讨了学习模型（包括神经网络）在多大程度上可以用来代替传统的 B 树到 Bloom-filter 的索引结构。 这似乎与直觉相反，因为机器学习并不提供传统的索引数据结构的输入输出，并且因为最强大的机器学习模型，神经网络的计算一般认为是非常昂贵的。 然而，我们认为，这些明显的障碍都不像它们看起来那么坑爹。 相反，我们使用学习模型的方式可能会带来巨大的好处，特别是在下一代硬件上。

就输入输出的语义来说，索引在很大程度上已经是学习模型，使得用神经网络等其他类型的模型取代它们变得非常简单。 例如，B 树可以被看作是一个模型，它将一个键 (Key) 字作为输入并预测数据值记录 (Value) 的位置。 Bloom-Filter 是一个二元分类器，它基于一个键 (Key) 来预测键 (Key) 是否存在于一个集合中。 显然，这就存在微妙但重要的差异。 例如，Bloom-filter 可能有假阳性 (false positives)，但没有假阴性 (false negatives)。然而，正如我们将在本文中展示的那样，可以通过新颖的学习技术和 / 或简单的辅助数据结构解决这些差异。

在性能方面，我们观察到每个 CPU 都具有强大的 SIMD 功能，并且我们推测许多笔记本电脑和手机很快将拥有图形处理单元（GPU）或张量处理单元（TPU）。 推测 CPU-SIMD / GPU / TPU 的功能将越来越强大，这是合理的，因为比通用指令集更容易扩展神经网络使用的有限的（并行）数学运算。 这样，今后执行神经网络的高成本在未来可能实际上可以忽略不计。例如，Nvidia 和 Google 的 TPU 已经能够在单个指令周期中执行数千次（如果不是数万次）神经网络操作 [ 3 ] 。 此外，有人表示，到 2025 年，GPU 的性能将提高 1000 倍 ，而 CPU 发展已经停滞，不按摩尔定律发展 [ 5 ] 。通过用神经网络取代重分支的索引结构，数据库可以从这些硬件趋势中受益。

重要的是要指出，我们并不主张用学习索引结构来完全取代传统的索引结构。 相反，我们概述了一种建立索引的新方法，它补充了现有的工作，并且可以说为一个有数十年历史的领域开辟了一个全新的研究方向。 虽然我们专注于分析只读工作负载，但我们还概述了如何将这种想法扩展到对写入频繁工作负载的索引做加速。 此外，我们简要概述如何使用相同的原则来替换数据库及其他组件的操作，包括排序和联表 (join)。 如果成功，这可能导致未来数据库的开发方式和现在彻底不同。

本文的其余部分概述如下：在下一节中，我们以 B 树为例介绍学习索引的总体思路。 在第 4 节中，我们将这个想法扩展到 Hash 索引，并在第 5 节中扩展到 Bloom-Filters。 所有部分都包含单独的评估和列出未解决的挑战。最后在第 6 部分我们讨论相关的工作，并在第 7 部分结束。

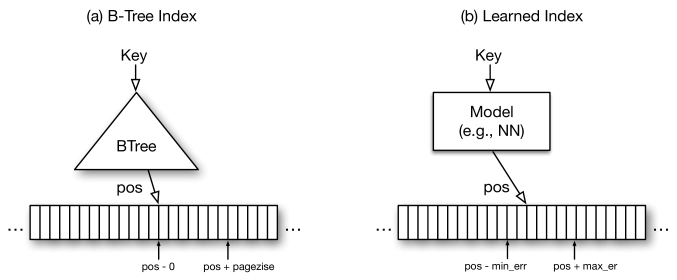
图1：为什么B 树是模型

2. 范围索引

索引结构已经是模型，因为它们可以“预测”给定键 (Key) 的值的位置。 要看到这一点，请在主键 (Key) 已排序的分析内存数据库（即只读）中考虑一个 B 树索引，如图 [1]（a）所示。 在这种情况下，B-Tree 提供从查找键 (Key) 到排序的值记录 (Value) 阵列内的位置的映射，并保证值记录 (Value) 位置大于等于查找到的位置。 请注意，必须对数据进行排序以允许范围请求。 还要注意，这个相同的一般概念适用于次级索引，其中底层将是 <key，pointer> 对的列表，其中键 (Key) 是索引属性的值，指针是对值记录 (Value) 的引用。

出于效率的原因，通常不会对已排序值记录 (Value) 的每个关键 (Key) 字进行索引，而只是每个 n 个值记录 (Value) 的一个键 (Key)，即每页面的第一个键 (Key)。 [2] 这有助于显着减少索引必须存储的键 (Key) 数量，而不会有任何显着的性能损失。 因此，B 树是一个模型，在 ML 术语中是回归树：它将键 (Key) 映射到具有最小和最大误差的位置之间（最小误差 0，最大误差页面大小）并保证可以在该地区找到该键 (Key) 锁对应的值记录 (Value)（如果存在）。 因此，我们可以用其他类型的机器学习模型（包括深度学习模型）取代 B 树索引，只要它们也能够提供类似的有关最小误差和最大误差的有力保证。

乍一看，可能很难为其他类型的 ML 模型提供相同的错误保证，但它实际上非常简单。 B-Tree 仅为存储的数据提供这种保证，而不是针对所有可能的数据。 对于新数据，B 树需要重新平衡，或者在机器学习的术语里面叫重新训练，通过训练来提供相同的误差保证。 这就极大地简化了问题：最小误差和最大误差是经过训练的（即存储的）数据的最大误差。 也就是说，我们唯一需要做的就是对每个键 (Key) 执行训练，并记住一个位置的最好和最差的位置预测。 给定一个键 (Key)，该模型预测哪里能找到相应的值记录 (Value); 如果键 (Key) 存在，则保证处于由最小和最大误差定义的预测范围内。 因此，我们能够用任何其他类型的回归模型（包括线性回归或神经网络）代替 B 树（见图 [1]（b））。

现在，我们需要解决其他技术挑战，然后才能使用学习好的索引替代 B 树。 例如，B 树具有插入和查找的有限成本，并且在利用缓存方面特别好。 此外，B 树可以将键 (Key) 映射到未连续映射到内存或磁盘的页面。 此外，如果查找关键 (Key) 字不存在于集合中，某些模型可能会返回最小 / 最大错误范围之外的位置，如果它们不是单调递增的模型。所有这些都是有趣的挑战 / 研究问题，会在本节中与潜在解决方案一起详细解释。

同时，使用其他类型的模型，特别是深度学习模型作为索引可以提供巨大的好处。 最重要的是，它有可能把 B 树 log n 查找成本为一个常数。 例如，假定数据集具有 1M 个唯一键 (Key)，大小在 1M 和 2M 之间（因此 1,000,009 存储在第 10 个位置上）。 在这种情况下，一个简单的线性模型，由一个单一的乘法和加法组成，可以完美地预测任何键 (Key) 的位置，而 B 树会需要做一个 log n 操作。 机器学习，尤其是神经网络的优点在于，他们能够学习各种各样的数据分布 / 混合和其他数据特征和模式。 显然，挑战在于平衡模型的复杂性与准确性。

2.1 我们可以承受模型有多复杂？ 来做个估算吧

为了更好地理解模型的复杂性，需要知道同样的一段时间内，遍历 B 树可以执行多少操作，以及学习索引需要达到什么样的精度来超过 B 树的精度。

考虑一个 B 树索引 100M 值记录 (Value)，页面大小为 100（译注：也就是单个节点的子节点数量，国内有翻译为阶的）。我们可以将每个 B-Tree 节点视为划分空间的一种方式，减少“误差”并缩小区域以查找数据。 因此，我们说 B-Tree 的页面大小为 100，每个节点的查找精度为 1/100 ，所以我们需要遍历 log(100, N) 个节点。 因此，第一个节点将查找空间从 100 M 缩小到 100 M / 100 = 1 M ，第二个节点从 1 M 到 1 M / 100 = 10 k 等等，直到找到值记录 (Value) 为止。 同时，遍历单个 B-Tree 页面需要大约 50 个时钟周期（我们测量了对超过 100 个缓存驻留记录的二分查找与遍历查找具有大致相同的性能），并且非常难以并行化 [3]。 相比之下，现代 CPU 可以在每个周期执行 8-16 个 SIMD 操作。 因此，只要学习索引模型的 查找精度 / 运算数 超过 (1/100) / 50 * 8 = 400 个算术运算，学习索引模型就会更快（译注：这里隐含了一个公式，查找速度 = 查找精度 / 运算数，也就是单位时间内的 查找概率）。 请注意，这个估算仍假定所有 B 数的页都在缓存中。 单个缓存未命中花费 50-100 个额外的周期，因此可以允许更复杂一些的模型。

此外，机器学习的快速发展正在彻底改变游戏。 它们允许在相同的时间内运行更复杂的模型，并从 CPU 中卸载计算（到 GPU 或 TPU 上）。 例如，NVIDIA 最新的 Tesla V100 GPU 能够实现 120 TeraFlops 的低精度的深度学习算术运算（每个时钟周期≈60,000 次运算） [ 7 ]。 假设整个学习索引都载入了 GPU 的内存（我们在 3.6 节中展示这是一个非常合理的假设），在 30 个时钟周期内，我们可以执行 100 万次神经网络操作。 当然，传输输入和从 GPU 获取结果的延迟仍然明显较高，大约为 2 微秒或数千个时钟周期，但这个问题并非不可克服，可以通过批处理方式，或者更加紧密的集成 CPU/ GPU / TPU [ 4 ] 。 最后，可以预期，GPU / TPU 每秒的浮点 / 整型操作的能力和数量将继续增加，而提高 CPU 执行 if 语句性能的进展基本上停滞不前 [ 5 ]。 尽管我们认为 GPU / TPU 是实践中采用学习索引的主要原因，但本文中我们将重点放在有限的 CPU 能力上，以便更好地研究通过机器学习取代 / 增强索引的影响，排除硬件更改的因素。

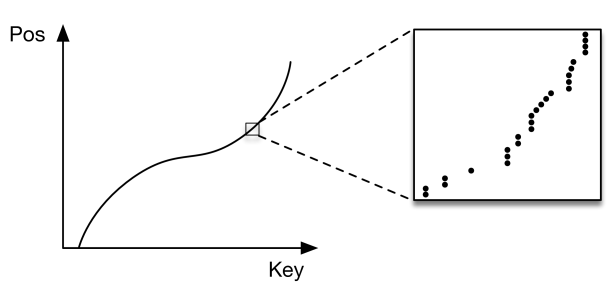
图2：作为CDF 的索引

2.2 范围索引模型是 CDF 模型

正如本节开头所述，索引是一个模型，它将一个键 (Key) 字作为输入并预测值记录 (Value) 的位置。 而对于单点查询，值记录 (Value) 的顺序并不重要，对于范围查询，必须根据查找关键 (Key) 字对数据进行排序，以便可以有效地检索范围内（例如，时间范围内）的所有数据项。 这导致了一个有趣的观察：预测给定排序数组内键 (Key) 的位置的模型有效地近似于累积分布函数（CDF）。 我们可以建模数据的 CDF 来预测位置：

其中p 是位置估计， F (Key) 是小于或等于查找键(Key) 的数据出现的概率，也就是累积分布函数(CDF, estimated cumulative distribution function, 详见这篇)，N 是键(Key) 的总数量（另见图[2]）。 这个观察开辟了一套全新的有趣方向：首先，它意味着任何一种索引字面上都需要学习数据分布。 B 树通过构建回归树来“学习”数据分布。 线性回归模型将通过最小化线性函数的(平方) 误差来学习数据分布。 其次，估计数据集的分布是一个众所周知的问题，学习索引可以从之前数十年的研究中受益。 第三，学习CDF 对优化其他类型的索引结构和潜在算法也起着关键作用，我们将在本文后面概述。

2.3 第一个，粗糙的学习索引

为了更好地理解用学习索引取代传统 B 树有哪些技术要求，我们使用了 200M Web 服务器日志值记录，目标是使用 Tensorflow [ 9 ] 在时间戳上建立二级索引。 我们使用 ReLU 激活函数训练了每层 32 个神经元（即 32 个宽度）的双层全连接神经网络 ; 时间戳是输入要素，位置是标签。

之后，我们使用 Tensorflow 和 Python 作为前端，测量随机选择的键的查找时间 (排除一开始跑的一些数据)。 在这种情况下，我们实现了每秒≈1250 次预测，即，使用 Tensorflow 执行模型需要≈80,000 纳秒 (ns)，甚至没算搜索时间。 预测对全量遍历几乎没有什么帮助。 作为比较，B 树遍历同样数据只需要≈300 ns， 小两个数量级，搜索键 (Key) 空间时，并且快 2-3 倍 。 其原因是多方面的：

1. Tensorflow 旨在有效地运行较大的模型，而不是小型模型，因此具有显着的调用开销，尤其是在 Python 作为前端时。
2. 一般来说，B 树，或者一般意义上的决策树，使用少量的操作就能过拟合数据，因为它们使用简单的 if 语句递归地分割空间。 相比之下，其他模型可以更有效地估计 CDF 的总体形状，但在单个数据实例级别的精确定位上有障碍。 要看到这个，请再次看看图 [2] 。 该图表明，从大的视图看，CDF 函数看起来非常平滑和规则。 但是，如果放大单个值记录 (Value)，越来越多的非规律显示出来 ; 一个众所周知的统计效应。 许多数据集恰恰具有这种行为：从大局看，数据分布显得非常平滑，而越放大越难接近 CDF，由于个体层面上的“随机性”。 因此，像神经网络，多项式回归等模型可能需要更多的 CPU 和空间从整个数据集缩小到到数千项中选择单个（译注，这里也就是在上文中指的预测误差，min/max error），单个神经网络通常需要更多的空间和 CPU 时间为“最后一公里”减少从数千到数百的误差。
3. 典型的 ML 优化目标是最小化平均误差。 但是，对于索引，我们不仅需要猜测项目的最佳位置，而且还需要实际找到它，但前面讨论的最小和最大误差率更重要。
4. B- 树的缓存效率非常高，因为它们始终将顶层节点保存在缓存中，并在需要时访问其他页面。 但是，其他模型并不像缓存和操作高效。 例如，标准神经网络需要所有权重参数来做预测，这种预测需要大量的乘法和权重参数，必须从内存中读入到缓存 (译注，这里和上面的缓存都是指 CPU 高速缓存)。

3. RM 索引 (Recursive-model，递归模型)

为了克服挑战并探索模型作为索引替代或丰富的潜力，我们开发了学习索引框架 （LIF），递归模型索引（RMI）和基于标准误差的搜索策略。 我们主要关注简单的全连接神经网络，因为它们的简单性，但其他许多类型模型也是可能的。

3.1 学习索引框架（LIF）

LIF 可以看作是一个索引合成系统或者说索引工厂 ; 给定一个索引规范， LIF 生成不同的索引配置，优化它们并自动化测试它们。 虽然 LIF 可以即时学习简单模型（例如，线性回归模型），但它依赖于更复杂模型（例如 NN）的 Tensorflow。 但是，它从不使用 Tensorflow 进行推理。 相反，给定一个经过训练的 Tensorflow 模型， LIF 会自动从模型中提取所有权重，并根据模型规范在 C ++ 中生成高效的索引结构。 虽然使用 XLA 的 Tensorflow 已经支持代码编译，但其重点主要放在大规模计算上，其中模型的执行时间量级是微秒或毫秒。 相比之下，我们的代码生成专注于小型模型，因此必须消除 Tensorflow 管理大模型的开销。 这里我们利用来自 [ 21 ] 的想法，它已经展示了如何避免 Spark 运行时不必要的开销。 因此，我们能够执行 30 纳秒级的简单模型。

3.2 递归模型索引

如第 2.3 节所述，构建替代 B 树的替代学习模型的关键挑战之一是最后一英里的准确性。 例如，使用单个模型把误差从 100M 减少到几百这个数量级是非常困难的。 同时，将误差从 100M 降低到 10K，例如 100 * 100 = 10000 的精度实现起来还简单些，这样就可以用简单模型替换 B-Tree 的前两层。 同样的，将误差从 10k 降低到 100 是一个更简单的问题，因为模型只需要关注数据的一个子集。

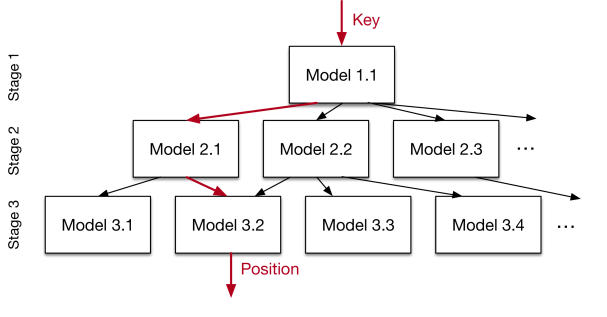
基于这种观察并受到专家们的共同努力 [ 51] 的启发，我们提出了递归回归模型（参见图 [3]）。 也就是说，我们构建了一个模型层次结构，其中模型的每个阶段都将键 (Key) 作为输入，并基于它选择另一个模型，直到最终预测到位置。 更正式地说，对于我们的模型 f(x) ，其中 x 是键， y∈ [ 0 ， N ) 位置，我们假设在阶段ℓ有 M 个模型。 我们在阶段 0 训练模型， \(f_0(x) ≈y\)。 因此，阶段ℓ中的模型 k，可以写成由\(f_ℓ^{(k)}\) 表示 ，并且被损失地训练，整个误差可以表示为如下公式：

注意，我们在这里使用这里的符号\(f_{ℓ-1}(x)\) 递归执行，这样

总而言之，我们用迭代地训练每个阶段，误差为\(L_ℓ\)，以建立完整的模型。

图3：分阶段模型

理解多个不同模型的一种方法是，每个模型都会对关键位置进行一定的预测误差，并使用预测来选择下一个模型，该模型负责将键(Key) 空间的某个区域以较低的误差做出更好的预测。 然而，要注意，递归模型索引不是树 。 如图[ 3 ] 所示，一个阶段的不同模型可能会在下面的阶段选择相同的模型。 此外，每个模型并不一定像B-Tree 那样包括同样数量的记录（即页面大小为100 的B 树覆盖100 个或更少的记录）。 4 最后，取决于所使用的模型，不同阶段之间的预测不一定会被解释为位置估计，而应该被视为挑选对某些键有更多认知的专家（另见[ 51 ] ）。

这种模型体系结构有几个好处：(1) 它利用了这一事实，即易于学习数据分布的整体形状。(2) 它的体系结构有效地将空间划分为更小的子空间，就像B 树/ 决策树那样，通过更少的操作更容易地实现所需的“最后一英里”精度。 (3) 在阶段之间不需要搜索过程。 例如， 模型1.1 的输出y 是一个偏移量，它可以直接用于在下一阶段中选择模型。 这不仅减少了管理数据结构的指令数量，而且还允许将整个索引表示为稀疏矩阵乘法跑到TPU / GPU 上。

3.3 混合索引

递归模型索引的另一个优点是，我们能够建立模型的混合。 例如，在顶层，一个小的 ReLU 神经网络可能是最好的选择，因为它们通常能够学习大范围的复杂数据分布，模型层次结构底部的模型可能有数千个简单的线性回归模型，因为它们在空间和执行时间都不贵。 此外，如果数据特别难以学习，我们甚至可以在最后阶段使用传统的 B 树。

对于本文，我们只关注 2 种模型，简单的神经网络，具有 0 到 2 个完全连接的隐藏层和 ReLU 激活函数，以及多达 32 个神经元和 B 树（也就是决策树）的层宽度。 给定一个索引配置，它指定阶段的数量和每个阶段的模型数量作为一个数组，混合索引的端到端训练按照算法 1 完成

 
    Algorithm 1: Hybrid End-To-End Training
    Input: int threshold, int stages[], NN complexity
    Data: record data[], Model index[][]
    Result: trained index
 
     1 M = stages.size;
     2 tmp records[][];
     3 tmp records[1][1] = all data;
     4 for i  <- 1 to M do
     5	for j <- 1 to stages[i] do
     6		index[i][j] = new NN trained on tmp records[i][j];
     7		if i < M then
     8 			for r ∈ tmp records[i][j] do
     9 				p = f(r.key) / stages[i + 1];
    10 				tmp records[i + 1][p].add(r);
    11 for j <- 1 to index[M].size do
    12 		index[M][j].calc_err(tmp records[M][j]);
    13 		if index[M][j].max abs err > threshold then
    14 			index[M][j] = new B-Tree trained on tmp records[M][j];
    15 return index;
 
 

从整个数据集（第 3 行）开始，它首先训练顶级节点模型。 根据这个顶级节点模型的预测，它会从下一阶段（第 9 行和第 10 行）中选取模型，并添加属于该模型的所有键（第 10 行）。 最后，在混合指标的情况下，如果绝对最小 / 最大误差高于预定义阈值（第 11-14 行），则通过用 B 树代替 NN 模型来优化指数。

请注意，我们在最后阶段为每个模型存储标准误差和最小误差和最大误差。 这样做的好处是，我们可以根据每个键 (Key) 的使用模型单独限制搜索空间。 此外，人们可能会想知道具体如何设置混合端到端训练的各种参数，包括阶段的数量和宽度，神经网络配置（即隐藏层数和宽度）以及何时替换节点的阈值为一棵 B 树。 通常，这些参数可以使用简单的网格搜索进行优化。 此外，可以根据时间来限制搜索空间（找到这些参数）。 例如，我们发现阈值为 128 或 256（B 树的典型页面大小）效果很好。 此外，对于 CPU，我们基本负担不起 1 或 2 个完全连接的隐藏层以及每层 8 至 128 个神经元的神经网络。 最后，考虑到模型的容量较低，可以用较小的数据样本训练较高层的阶段的模型，这显然加快了培训过程。

请注意，混合索引允许我们将学习索引的最差情况性能与 B 树的性能相关联。 也就是说，在学习不到数据分布的情况下，所有模型都会被 B-Trees 自动替换，实际上是一个完整的 B-Tree（阶段之间有一些额外的开销等等，但是性能是总体相似）。

3.4 搜索策略

要在叶页中查找实际记录，对于小数据量，无论是二进制搜索还是全量扫描通常都是最快的策略 ; 尽管（业内）作出了许多尝试，但反复的结果表明， 其他搜索策略由于其额外的复杂性而没有提供什么（如果有的话）益处 [ 8 ]) ] 。 再一次，学习索引在这里也可能具有优势：模型实际上预测了键 (Key) 的位置，这可能更接近值记录 (Value) 的实际位置，而用最小 / 最大误差会差的更远些。 这就是说，如果我们可以利用这样一个事实，即在位置估计最小误差和最大误差范围内，我们对位置进行了良好估计，那么我们可能能够找到记录（或 <= 查找键的键）比传统的二进制搜索更快。 因此我们制定了几种搜索策略。

模型二进制搜索：我们的默认搜索策略，和传统的二分搜索策略的唯一区别在于，把第一个中间点设为模型预测的值。

偏见搜索：这种搜索策略修改了我们的模型二分搜索，在每次迭代中不会平均分割从中间点到左侧和右侧的距离。 相反，新中间值取决于最后阶段的模型的输出的标准偏差σ 。 例如，如果确定键 (Key) 大于中间值 ，则将新中间值设置为 min(middle+σ,(middle+right)/2)。

偏见四元搜索：最后，我们开发了一种新的搜索策略，在任何迭代中都不会选择一个新的中间值来进行二分搜索，而是用了三个新的数据点，即所谓的四元搜索。 研究人员过去尝试四元搜索的主要原因是因为它可以提供更好的预取行为。 也就是说，首先计算三个“中间”点，由使用 CPU intrinsics 来计算。 之后才会测试不同的“中间”点，并根据结果进行搜索的下一次迭代，非常类似于二分查找。 如果 CPU 能够从主存储器 (Memory) 中并行获取多个数据地址，那么这种策略可能更好，但据报道实际上这种策略大部分与二进制搜索相同 [ 8 ] 。 然而，再次有一个更好的位置估计可能会有所帮助：也就是说，我们将我们最初的三个四元搜索中点定义为 pos - σ ， pos ， pos + σ 。 我们假设，大部分预测都是准确的，首先关注位置估计，然后继续传统的四元搜索。

3.5 索引字符串

我们主要关注索引真正有值记录 (Value) 的键 (Key)，但许多数据库依赖索引字符串，幸运的是，有不少重要的机器学习研究聚焦在字符串建模上。 和以前一样，我们需要设计一个高效但有表现力的字符串模型。 对字符串做好这个设计会带来许多独特的挑战。

第一个设计考虑是如何将字符串转换为模型的特征，通常称为标记化。 为了简单和高效，我们认为 n 长度的字符串是长度为\(x∈\mathbb{R}^n\) 的特征向量，其中\(x_i\) 是第 i 位的字符的 ASCII 十进制值（或者取决于字符串的 Unicode 十进制值）。 此外，如果所有输入的尺寸相同，大多数 ML 模型的运行效率会更高。 因此，我们将设置最大输入长度 N。 由于数据按字典顺序排序，我们将在标记化之前将键截断为长度 N. 对于长度为 n < N 的字符串，我们为 i > n 设置\(x_i = 0\) 。

为了提高效率，我们通常采用与我们针对数据特征相似的建模方法。 我们学习了一个相对较小的前馈神经网络的层次结构。 一个区别是输入不是一个单一的实数值 x，而是一个向量x 。 线性模型w⋅x + b随着输入长度 N 线性地增加乘法和加法的计算数量。 前馈神经网络，带有一个宽度为 h 的隐藏层，也会扩展到 O(hN) 乘法和加法计算数量。（在与 N 无关的更深层网络中可能会有额外的复杂性）。

这种方法有一些有趣的特性，表明了设计字符串 CDF 的一般 ML 模型的困难。 如果我们考虑长度为三的八个字符串，字符串里面的字符是 [0,8) ，那么我们可以容易地对位置建模为 \(4 x_0 + 2 x_1 + x _2^5\) 。 但是，如果我们看看 Unix 字典的编码，我们会发现数据更加的复杂。 以“s”以“e”开头的单词是其他单词的三倍，这样甚至对单词里面的第一个字符就没法线性建模。 此外，字符之间存在相互作用 - 大约 10％以“s”开头的单词以“sh”开头，而以“e”开头的单词只有 0.1％以“eh”开头. DNN 算法，如果足够宽或足够深，可以成功地对这些相互作用进行建模，更常见的是，递归神经网络（RNN）在建模文本中显示出非常成功。

最终，我们相信未来会有相当好的研究可以优化字符串的学习索引。 例如，我们可以轻松想象其他标记化算法。 在字符串标记化的自然语言处理方面有大量研究将字符串分解为 ML 模型中更有用的部分，例如机器翻译中的字词 [ 59] 。 此外，还有大量关于特征选择的研究选择最有用的特征子集，从而限制模型需要处理的特征的数量。 此外，GPU 和 TPU 需要相对较大的模型，因此可以无缝扩展字符串长度增加的场景，及许多更复杂的模型体系结构（例如递归和卷积神经网络）中。

3.6 结果

为了将学习指标与 B 树进行比较，我们在 3 个实际数据集上创建了 4 个二级索引：（1）Weblogs，（2）地图数据集 [ 46] 和（3）web 文档以及 1 个合成数据集（4）正态对数。 Weblogs 数据集包含 200 M 日志条目，是多年来对主要大学网站的每个 web 请求，并对唯一时间戳进行主索引。 该数据集对于学习索引来说几乎是一种最坏的情况，因为它包含由课程安排，周末假期，午餐休息，部门活动，学期休息等引起的非常复杂的时间模式，这是众所周知的难以学习的。 对于地图数据集，我们将世界各地≈200M 用户维护特征（例如道路，博物馆，咖啡店）的经度编入索引。 不出所料，位置的经度相对线性，并且比 weblog 数据集的不规则性更少。 web 文档数据集由大型互联网公司的真实产品组成部分的大型网络索引的 10 M 个非连续文档 ID 组成。 最后，为了测试索引如何处理重尾分布，我们生成了一个从μ = 0 和σ = 2 的对数正态分布中抽取的 190M 独特值的综合数据集。 这些值被放大到整数 1Billon。 这些数据当然是高度非线性的，这使得 CDF 使用神经网络学习更加困难。

对于所有数据集，我们使用不同页面大小的 B 树和不同的第二阶段大小（即 10k，50k，100k 和 200k 模型数量）的 RMI学习索引进行比较。 我们的 B 树实现类似于 stx :: btree，但做了进一步的行缓存优化，在一个针对 FAST 的微基准 [ 36] 对比测试中性能很强，在这个测试中把我们的 B- 树和一个把 SIMD 优化用的出神入化的 B 树作比较，跑起来差不多。我们使用简单的网格搜索，基于简单模型来调整两阶段模型。 也就是说，我们只尝试了具有零到两个隐藏层的神经网络和层数为 4 到 32 个节点的神经网络。 一般而言，我们发现，对于第一阶段而言，简单的（0 隐藏层）到半复杂（2 隐藏层，8 或 16 宽）模型效果最好。 对于第二阶段来说，它变成了我们的简单（0 隐藏层），它们基本上是线性模型，具有最佳性能。 这并不令人惊讶，因为对于最后一英里来说，执行复杂模型往往是不值得的，线性模型可以被最优学习。最后，我们所有学习的索引模型都使用 LIF 进行编译，并且我们只显示具有 32GB RAM 的 Intel-E5 CPU 上性能最佳的模型的数字， 而不使用 GPU / TPU，进行超过 30M 次的查找，重复 4 次。

加载时间：虽然本文的重点不在加载或插入时间，但应该注意的是，大多数模型可以训练得相当快。 例如，如果在 C ++ 中实现，那么无需隐藏层的模型可以在几秒钟内在超过 200M 条记录上进行训练。 但是，对于更复杂的模型，我们选择使用 Tensorflow，由于其开销，花费了更长的时间。然而，我们相信我们可以相对较快地对超参数空间进行网格搜索，大约需要分钟数量级跑简单模型。 此外，可以使用诸如 [ 52 ] 之类的自动调整技术来进一步缩短查找最佳索引配置所需的时间。

3.6.1 整数数据集

图4：地图数据：学习索引与B-Tree

图5： Web 日志数据：学习索引与B-Tree

图6：正态分布的对数数据集：学习索引与B-Tree

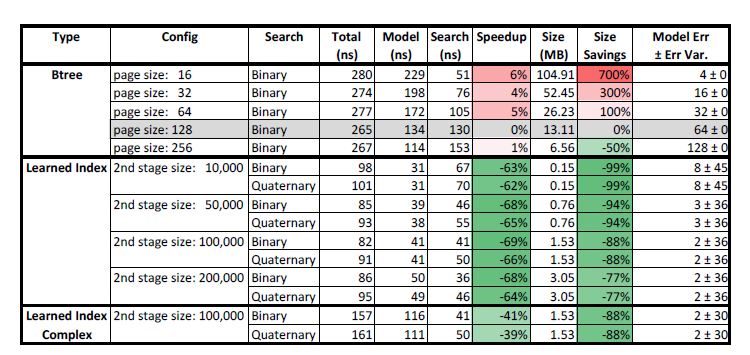
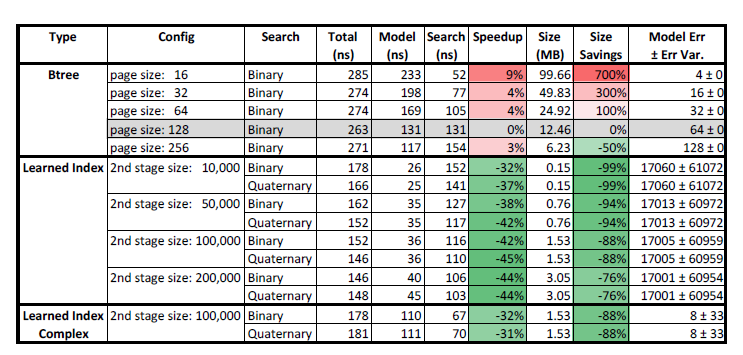
图[4]，图[5] 和图[6] 分别显示了两个真实世界整数数据集（地图和博客）和合成数据（对数正态数据）的结果。 作为主要指标，我们将总查找时间分解为模型执行（B 树遍历或ML 模型）和本地搜索时间（例如，在B 树叶子页面中查找键(Key)）。 另外，我们记录了索引结构的大小（不包括排序数组的大小），空间节省和模型误差及其误差方差。 模型误差是最后阶段所有模型的平均标准误差，而误差方差则表明这些标准误差在模型之间有多大变化。 请注意，对于B-Tree 而言，由于没有阶段，所以它始终是一个取决于页面大小的固定误差。 加速和大小列中的颜色编码指示索引相对于页面大小为128 的高速缓存优化的B 树索引的基线有多快或多慢（更大或更小）。

可以看出，在几乎所有配置中，学习索引比B 树要快，速度提高了3 倍 ，并且达到了数量级的更小。 当然，B 树可以以CPU 时间为代价进一步压缩以进行解压缩。 然而，大多数优化不仅是正交的（可以用在神经网络上），而且对于神经网络来说，存在更多的压缩潜力。 例如，神经网络可以通过使用4 或8 位整数而不是32 或64 位浮点值来表示模型参数（一种称为量化的过程）进行压缩。 与B 树压缩技术相反，这实际上可以进一步加速计算。

有趣的是，四元搜索仅对某些数据集有帮助。 例如，它对weblog 和log-normal 数据集有一点帮助，但对地图数据集没有帮助。 我们没有报告偏见搜索和B 树，或者不同搜索策略的结果差异，因为它们没有为数字数据集提供任何好处。 值得注意的是，模型的准确性也有很大差异。 对于合成数据集和博客数据的来说，误差要高得多，这会影响搜索时间。 作为比较，我们搞了一个学习索引，有更复杂的第一阶段模型（“学习索引复合体”），该索引有2 层完全连通的隐藏层和每层16 个神经元，可以大幅的减少误差。 然而，在CPU 上，模型的复杂性并没有得到回报（例如，模型执行时间太长，无法证明搜索时间较短）。 然而，正如前面提到了GPU / TPU 的发展，这种trade-off 会被改变，我们推测下一代硬件对更复杂的模型有利。

可以观察到，第二阶段大小（模型数量）对索引大小和查找性能具有显着影响。 这并不奇怪，因为第二阶段决定了需要存储多少个模型。 值得注意的是，我们的第二阶段使用了10,000 或更多的模型。 这在第[2.1] 节的分析中特别令人印象深刻，因为它表明我们的第一阶段模型可以比B 树中的单个节点在精度上有更大的提高。

最后，我们没有提到整数数据集的上跑任何混合模型，因为它们像偏见搜索一样没有提供任何好处。

3.6.2 字符串数据集

图7：字符串数据：学习索引与B-Tree

图8：使用不同搜索策略的学习字符串索引

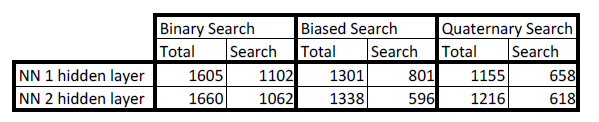
图[7] 显示了不同的搜索策略。 但是，我们确实在表格中看到最佳模型是一个非混合RMI 模型索引，使用四元搜索策略，名为“Learned QS”（表格底部）。 所有RMI 索引在第二阶段使用10,000 个模型，对于混合索引，我们使用两个阈值128 和64，作为模型在用B-Tree 替换自己之前的最大容许绝对误差。

可以看出，用于字符串的B-Trees学习索引的加速不再那么突出。 这因为一个事实——模型执行相当昂贵，这是GPU / TPU 可以解决的问题。 此外，搜索字符串要昂贵得多，因此更高的精确度通常会得到更好的结果。 这就导致了混合索引通过B 树取代表现不佳的模型，有助于提高性能。

最后，由于搜索成本的不同，如图[8] 所示，对于具有一个或两个隐藏层的2 级神经网络模型，不同的搜索策略会产生更大的差异。 请注意，我们没有为B 树显示不同的搜索策略，因为它们没有提高性能。 偏见搜索和四元搜索性能更好的原因是他们可以将标准误差考虑在内。

3.7 未来的研究挑战

到目前为止，我们的结果集中在只读内存数据库系统的索引结构上。 正如我们已经指出的那样，即使没有任何重大修改，当前的设计已经可以替代数据仓库中使用的索引结构，这些索引结构可能每天只更新一次，或者 BigTable [ 18 ] ，其中创建 B 树批量作为 SStable 合并过程的一部分。 在本节中，我们将概述如何将学习型索引结构的概念扩展到频繁插入的工作负载场景下。

3.7.1 插入和更新

初看起来，由于学习模型潜在的高成本，插入似乎是学习索引的致命弱点，但是再次，学习索引对于某些工作负载可能具有显着的优势。 一般来说，我们可以区分两种类型的插入：（1）appends 和（2） inserts in the middle，例如在订单表上更新客户 id 上的二级索引。 现在我们关注后者，并考虑在我们的已排序数据集中引入额外空间的方法，类似于 B 树通过其每个页面的最小和最大填充因子在已有页面中引入额外空间。 但是，与 B 树相反，假设我们不会均匀地分散空间，而是依赖于学习的累积密度函数。 最后，假设插页大致遵循与学习的 CDF 相似的模式 ; 这并不是一个不合理的假设，就像在顾客 id 的二级索引的例子中，顾客大致会保持购物行为。在这些假设下，模型可能根本不需要再培训。 这样，对新项目的插入，学习索引可以“概括”成为 O(1) 操作，因为它们可以直接放入可用空间中，并且空间可用于最常用位置。 相反，B- 树需要 O (log n) 用于查找和重新平衡树的插入操作（特别是插入某个区域比其他区域更普遍）。 类似的，对于追加插入，如果模型能够学习新数据的关键趋势，模型也可能不需要重新学习。

显然，这一观察结果也提出了几个问题。 首先，模型的普遍性和“最后一英里”表现似乎有一个有趣的折衷 ; “最后一英里”预测越好，可以说，模型过度拟合的能力越强，而且对新数据项的适应能力也越低。

其次，如果分布发生变化会发生什么？ 它是否可以被检测到，并且是否有可能提供与 B 树一样的强力保证，它总是能够保证 O(log n) 的查找和插入成本？ 虽然回答这个问题已经超出了本文的范围，但我们相信某些模型有可能实现它。 考虑一个简单的线性模型：在这种情况下，插入的项目绝不会将误差增加超过 max_abs_error + 1 。 此外，重新训练线性模型的成本为\(O(K_{M + 1})\) ，其中\(K_{M + 1}\) 是模型在数据中覆盖的项目数。如果线性模型不足以实现可接受的误差，我们可以将范围分成两个模型，并在上层的那个阶段重新训练模型。 这个模型可能需要重新训练\(O(K_{M})\)，其中\(K_{M}\) 是在重新训练第一个模型之后的最后一个阶段的模型数 M 等等。因此，基于第一个模型的再训练，容易限制绝对误差。 但是，为了给第一个模型提供一个很好的误差，我们可能需要增加模型的容量，例如通过添加一个多项式或一个额外的隐藏层。 这里有可能通过诸如 VC 维度的技术再次限制所需的复杂度增加。 研究这些影响，尤其是对于其他类型的模型，包括神经网络，留待未来的人们的工作。

处理插入的另一种更简单的方法是构建一个增量索引 [ 49 ] 和许多其他系统中，并且还具有如下优点：对于大型再训练操作，可以使用诸如 GPU / TPU 的专用硬件，这将显着加速，即使需要对整个模型重新训练也是如此。

最后，通过使用先前的解决方案作为起点，可以对每个模型的训练进行热启动。 特别是依赖梯度下降优化的模型可以从这种优化中获益 [ 33 ] 。

3.7.2 分页

在本节中，我们假定数据（实际记录或 <key，pointer> 对）存储在一个连续的块中。 但是，特别是对于存储在磁盘上的数据的索引，将数据分区为存储在磁盘上的不同区域中的较大页面是相当常见的。 为此，我们观察到一个模型学习 CDF 不再成立，因为\(p = F （ X < Key ） * N\) 被违反。 下面我们概述几个可以解决这个问题的方法：

利用 RMI 结构：RMI 结构已经将空间划分为区域。 通过对学习过程的小修改，我们可以最大限度地减少它们覆盖的区域中模型的重叠程度。 此外，可能会复制任何可能被多个模型访问的记录。 这样我们可以简单地将偏移量存储到模型中，也就是数据存储在磁盘上的位置。

另一种选择是以 <first_key，disk-position> 的形式提供额外的转换表。 通过转换表，索引结构的其余部分保持不变。 但是，这个想法只有在磁盘页面非常大的情况下才会起作用，如果不是千兆字节，则可能在几百兆字节，翻译表格就会太大。 同时，可以使用带有最小和最大错误的预测位置来减少必须从大页面读取的字节数，这样页面大小的影响可以忽略不计。

使用更复杂的模型，实际上可以学习页面的实际指针位置。 特别是如果使用文件系统来确定磁盘上的页面，并且在磁盘上有系统编号的块（例如， block1，…，block100 ），则学习过程可以保持不变。

显然，需要更多的研究来更好地理解基于磁盘的系统的学习索引的影响。与此同时，节省的大量空间以及速度优势，会让这个工作的未来很有趣。

4. 点索引

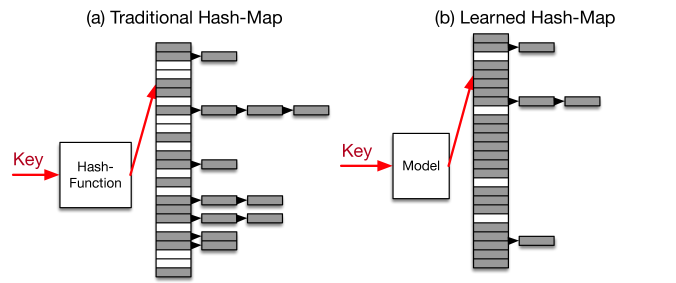
除了范围索引之外，点查找的 Hash Map 在 DBMS 中起着类似或更重要的作用。 从概念上讲，Hash Map 使用 Hash 函数来确定性地将键映射到数组内的随机位置（参见图 [9 ]，只有 4 位开销，但速度降低 3-7 倍。

图9：传统Hash 图与学习Hash 图

类似于B 树，机器学习模型可能会提供解决方案。 例如，如果我们可以学习一个将每个键唯一映射到数组内的唯一位置的模型，我们可以避免冲突（参见图[9] （b））。 尽管将模型学习为散列函数的想法并不新鲜，但现有工作主要集中在学习更好的散列函数以将对象从较高维空间映射到较低维空间以进行相似性搜索（即类似的对象具有相似的散列- 值） [55,57,32 ] 。 据我们所知，怎么通过学习产生更有效的点索引结构的模型，还没有被探索过。 虽然第一眼看起来似乎不可能使用机器学习模型来加速Hash Map，但如果内存空间是一个重大问题，它实际上可能是一种选择。 正如我们的实验所显示的，传统技术想达到高利用率（每个记录的小开销浪费空间小于20％）非常难以实现，而且会导致显着的性能损失。 相比之下，学习模型能够根据数据分布实现更高的利用率。 此外，还有可能将模型卸载到GPU / TPU，这可能会减轻通过散列函数执行模型的额外成本。

4.1 Hash 模型索引

令人惊讶的是，学习键 (Key) 的 CDF 分布是一种潜在的得到更好散列函数的办法。 然而，与范围索引相比，我们并不打算将记录紧凑或按严格排序顺序存储。 相反，我们可以通过 Hash Map 的目标大小 M 来缩放 CDF，并使用 h(K) = F(K) * M ，其中的 Key K 作为我们的 Hash 函数。 如果模型 F 完美地学习了 CDF，则不存在冲突。 此外，学习得到 Hash 函数与实际的 Hash Map 实现不冲突，并且可以与链表或任何其他方法结合使用。

对于模型体系结构，我们可以再次利用上一节中的递归模型体系结构。 很明显，和以前一样，在索引大小和性能之间存在一个折衷，这受到模型架构和数据集的影响。

请注意，Hash 模型索引的插入操作与正常 Hash 表的插入方式相同：使用 h(k) 对密钥进行 Hash 处理，并将项插入返回的位置。 如果该位置已被采用，则用普通 Hash Map 的实现确定如何处理冲突。 这意味着，只要插入数据的特征与现有数据类似，散列函数就会保持其效率。 但是，如果数据分布发生变化，则可能需要按照前面所述重新训练模型。 再次，这超出了本文的范围。

4.2 结果

图10：模型vs 随机Hash Map

为了测试使用机器学习模型的Hash 索引的可行性，我们徒手实现了基于链表的Hash Map; 记录(Value) 直接存储在Hash 表中，并且只有在冲突的情况下记录才会附加到链表。 没有冲突，最多只会发生一次缓存未命中。 只有在几个键(Key) 映射到相同位置的情况下，可能会发生额外的缓存未命中。 我们选择该设计，因为它可以实现最佳查找性能。 例如，我们还测试了商业级密集Hash 图,，使用桶策略和就地溢出（即，Hash Map 被分成桶以最小化开销，并在桶满时使用就地溢出[ 2 ] ） 。 虽然使用这种技术可以实现更小的内存占用，但我们发现它比链表方式慢两倍。 此外，在8 ％或更多的内存利用率下，密集的Hash-map 在性能上进一步降低。 当然，许多进一步的（正交）优化是可能的，并且我们绝不会声称这是Hash Map 的最大内存或CPU 高效实现。 相反，我们的目标是展示学习Hash 函数的一般潜力。

作为本实验的基准，我们使用Hash Map 实现和随机Hash 函数，该函数只使用两次乘法，3 次移位和3 次异或，这比加密Hash 函数快得多。 作为我们的模型散列函数，我们在第二阶段使用了与前一节中的100k 模型相同的2 阶段RMI 模型，没有任何隐藏层。 我们没有尝试任何其他模型，因为我们特别关注快速查找速度。

我们使用了与前一节相同的三个int 数据集，并且对于所有实验，我们改变了可用插槽的数量，从75 ％到125 ％数据数量。 也就是说， 75 ％的Hash 表中的插槽比数据记录少25 ％ 。 强制槽数量小于数据数量，可减少Hash 表中的空位，但会增加链接列表的长度。

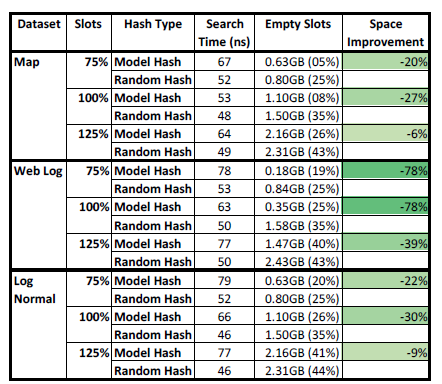
结果如图[10] 的平均查找时间，空槽数量（GB 单位）以及可用槽位总数的百分比和空间j 节约的改进。 请注意，与上一节相比，我们确实包含了数据大小 。 主要原因是，为了启用1 次缓存未命中查找，数据本身必须包含在Hash Map 中，而在上一节中，我们只计算了除排序数组本身之外的额外索引开销。

从图中可以看出，模型Hash 函数的索引总体上具有相似的性能，同时更好地利用内存。 例如，如果有100 ％的插槽数（即Hash 表中的插槽数与数据大小相匹配），随机Hash 总会经历大约35 ％的冲突（理论值为33.3 ％）并浪费1.5G B 的主存，而学习索引的散列函数更好地分散了密钥空间，因此能够将未使用的内存空间减少到高达80 ％ ，具体取决于数据集。

显然，当我们增加Hash 表的大小以增加25 ％的插槽时，节省量不会很大，因为Hash 表也可以更好地分散键(Key)。 令人惊讶的是，如果我们将空间减少到键的数量的75 ％ ，由于仍然起作用的生日悖论，学习的Hash 图仍然具有优势。 我们也做过更小尺寸的实验，观察到大约50 ％的大小插槽数在随机和学习Hash 函数之间没有明显差异。 但是，将Hash Map 大小减少为仅包含数据大小的一半时隙，链表变长，查找时间也会变长。

4.3 替代方法和未来工作

除了使用 CDF 作为更好的散列函数外，还可以开发其他类型的模型。 虽然不在本文的范围内，但我们在某种程度上探讨了共同优化数据放置和查找数据的功能。 然而，在许多情况下，事实证明，混合模型专家模式们对于许多数据集的表现最好。

此外，也可以像混合索引一样将 Hash-map 与模型更紧密地结合起来。 也就是说，我们可以学习模型的几个阶段，并用简单的随机 Hash 函数替换性能较差的模型（即那些产生比随机 Hash 更多冲突的模型）。 这样，最坏的情况下的性能将与随机 Hash 相似。 但是，如果数据具有可以学习的模式，则可以实现更高的内存利用率。

5. 存在索引

图11： Bloom filter 作为分类问题

DBMS 的最后一种通用索引类型是存在索引，最重要的是 Bloom-Filters，它是一种空间高效的概率数据结构，用于测试某个元素是否为集合的成员。 它们通常用于确定低温存储中是否存在键 (Key)。 例如，BigTable 使用它们来确定一个密钥是否包含在 SSTable [ 18 ] 中 。

在内部，Bloom filter 使用大小为 m 的位数组和 k 个哈希函数，每个函数将一个关键字映射到 m 个数组位置中的一个（参见图 [12]。

虽然 Bloom filter 非常节省空间，但它们仍可占用大量内存。 例如，想达到具有 0.1 ％的假阳性率（FPR）的 100M 记录，需要比记录大约多 14 倍的位。 因此，对于十亿个记录，大约需要大约 1.76 Gigabyte 个字节 (十亿 = \(10^9\) bit ， 位数 = \(14 * 10^9\) bit ≈ 1.76GB Byte )。 对于 0.01 ％的 FPR，我们需要≈2.23 Gigabyte。 有几次尝试来提高 Bloom filters 的效率 [ 43 ] ，但一般的开销依然存在。

然而，如果存在一些结构特性来确定什么是内部或外部的，用于学习，那么就可以构建更有效的表示。 有趣的是，对于数据库系统的存在索引，延迟和空间要求通常与我们之前看到的两种完全不同。 考虑到访问低温存储（例如磁盘甚至磁带）的高延迟，我们可以承担更复杂的模型，而主要目标是最小化索引的空间和误报的数量。

下面我们概述使用学习模型建立生存指数的两种潜在方法。

图12：具有学习散列函数的Bloom filter

5.1 学习索引版 Bloom filter

虽然范围和点索引都知道键的分布，但存在索引需要学习将键和其他所有内容分开的函数。 换言之，针对点索引的良好 hash 函数是密钥间几乎没有碰撞的散列函数，而 Bloom filter 的良好 hash 函数将是键 (Key) 间有很多冲突同时 非键 (Non-Key) 间也发生大量冲突的良好散列函数，但很少有键 (Key) 和非键 (Non-Key) 之间的冲突。 我们在下面考虑如何学习这样一个函数 f 以及如何将它合并到一个存在索引中。

传统上，存在指标不会猜测键 (Key) 的分布，也不会猜测键 (Key) 与非键 (Non-Key) 有什么不同。 例如，如果我们的数据库包含 0≤x<n 的所有整数 x ，则可以通过计算 f(x) ≡1 [0≤x<n] 来在恒定时间内计算存在索引，并且几乎没有存储器占用空间。 在考虑用于训练 ML(Machine Learning) 目的的数据分布时，我们必须考虑非键 (Non-Key) 的数据集 - 这可以是随机生成的键 (Key)，基于先前对存在索引的查询日志，或者由机器学习模型生成 [ 26]。 虽然 Bloom filter 保证任何一组查询的假阳性率（FPR）为一个特定值和假阴性率（FNR）为零，我们也遵循这样的概念，即我们希望为具体的实际查询提供特定的 FPR，并保持 FNR 为 0。

5.1.1 Bloom filters 作为分类问题

构建存在索引的另一种方法是作为二元分类任务。 也就是说，我们想要学习一个模型 f，它可以预测一个查询 x 是一个键 (Key) 还是非键 (Non-Key)。 为此，我们用这样的数据\(D = { (x_i,y_i = 1) | x_i ∈ K } ∪ {(x_i,yi) = 0)|x_i ∈ U}\)， 来训练一个神经网络。 由于这是一个二元分类任务，我们的神经网络使用 sigmoid 激活函数来产生一个概率，并通过训练以最小化对数损失，

如前所述，可以选择f 来匹配被索引的数据类型。 我们通常考虑递归神经网络（RNN）或卷积神经网络（CNN），因为它们已被反复证明是有效的字符串建模方式[ 54,29 ] 。

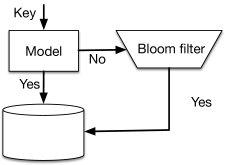
给定一个训练好的模型f ，我们如何使它成为一个有效率的存在索引？f (x) 的输出可以解释为x 是我们数据库中的一个键的概率; 我们必须选择一个阈值τ，高于此阈值我们将假定键(Key) 存在于我们的数据库中。 由于Bloom filter 通常针对特定的FPR 进行调整，因此我们可以将τ放在为在索引的查询数据集内，来动态实现所需的FPR。 与Bloom filter 不同，我们的模型可能同时具有非零FPR 和FNR; 事实上，随着FPR 的下降，FNR 将会上升。 为了保持存在索引不存在假阴性的约束，我们创建了一个溢出Bloom filter。 也就是说，我们考虑\(K^- _τ= { x∈K | f (x)< τ }\) 是f 的假阴性集合，并为这个键子集创建一个Bloom filters。 然后我们可以运行我们的存在索引，如图[11] 存在; 否则，检查溢出Bloom filter。

这种设置是有效的，因为学习模型相对于数据的大小可以相当小。 此外，由于Bloom filter 随着键(Key) 集合的大小线性缩放，溢出Bloom filter 将按照FNR 进行缩放。 也就是说，即使我们的假阴性率为50％，我们也会_ 将_ Bloom filter 的大小_ 减半_ （不包括模型大小）。 我们将通过实验发现，这种组合在降低存在索引的内存占用方面是有效的。 最后，学习模型计算可以受益于像GPU 和TPU 这样的机器学习加速器，而传统的Bloom filter 往往严重依赖于存储器系统的随机访问延迟。

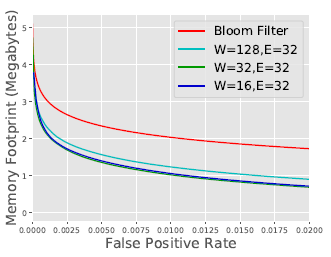
图13：了解的Bloom filter 可以在大范围的误报率下改善内存占用。 （这里W 是RNN 宽度， E 是每个角色的嵌入尺寸。）

5.1.2 带 Hash 模型的 Bloom filter

在分类问题的初始化设置中，我们选择一个阈值τ并且接受 f (x) ≥τ的预测将具有非零 FPR，并且具有 f (x)<τ的预测将具有非零 FNR。 这与 Bloom filter 中 Hash 函数的典型观点相矛盾，因为没有槽时应该具有非零的 FNR。 我们可以使用 f 作为这种散列函数，通过使用它来映射到大小为 m 的位数组。因为如上所述， f 将查询映射到范围 [0,1] ，所以我们可以假设函数 d 对该空间进行离散化。 例如，我们可以通过\(d§ = \lfloor mp\rfloor\) 来最简单地定义 d 。 因此，我们可以使用 d(f(x)) 作为散列函数，就像 Bloom filter 中的其他函数一样。 这具有以下优点： f 被训练成将大部分键 (Key) 映射到比特位置的较高范围以及将非键 (Non-Key) 映射到较低范围的比特位置。

5.2 结果

为了通过实验测试这个想法，我们探索了存在索引在追踪黑名单钓鱼网址方面的应用。 我们将 Google 透明度报告中的数据视为我们密切关注的一组键 (Key)。 该数据集由 1.7M 个唯一的 URL 组成。 我们使用的阴性 (也就是不在数据集里面的）网址，其中包含随机（有效）网址和列入白名单的网址，这些网址可能会被误认为是钓鱼网页。 我们训练一个 character-level 的 RNN（特别是 GRU [ 19 ] ）来预测 URL 属于哪一组。

具有期望 1％FPR 的常规 Bloom filter 需要 2.04MB。 我们考虑一个 16 维 GRU，每个角色 (character) 都有 32 维嵌入 ; 这个模型的大小是 0.0259MB。 我们发现，如果我们想强制执行 1％的 FPR，TNR 是 49％。 如上所述，我们的 Bloom filter 的大小与 FNR(51％) 一致。 因此，我们发现我们的模型 + 溢出 Bloom filter 使用了 1.07MB，大小减少了 47％。 如果我们想强制执行 0.1％的 FPR，我们的 FNR 为 71％，这使 Bloom Filter 的总大小从 3.06MB 降至 2.2MB，减少了 28％的内存。 我们观察图 [13 中的] 这种一般关系。 有趣的是，我们看到不同的尺寸模型如何在不同的精度和内存之间取得平衡。

显然，我们的模型越精确，Bloom filter 尺寸的节省就越好。 其中一个有趣的特性是我们的模型没有理由需要使用与 Bloom filter 相同的功能。 例如，已经有重要的研究在使用 ML 来预测一个网页是否是一个钓鱼页面 [ 10,13 ] 。 其他功能，如 WHOIS 数据或 IP 信息可以纳入模型，提高准确性，减少 Bloom filter 的大小，并保持没有误报的属性。

6. 相关工作

学习索引的思想建立在机器学习和索引技术的广泛研究之上。 以下，我们重点介绍最重要的相关领域。

B 树和变体：在过去的几十年中，已经提出了各种不同的索引结构 [ 28 ] 。

然而，所有这些方法都与学习索引的思想是正交的，因为他们都没有从数据的分布中学习，以实现更紧凑的指数表示或性能收益。 与此同时，正如我们的混合索引，可以将现有的硬件觉察索引策略与学习模型更紧密地结合起来，以获得进一步的性能提升。

由于 B + 树消耗大量内存，所以在压缩索引方面也有很多工作，如前缀 / 后缀截断，字典压缩，键 (Key) 规范化 [ 28,25,45] ）。 有趣的是，一些现有的压缩技术与我们的方法相辅相成，可以帮助进一步提高效率。 例如，字典压缩可以看作是一种嵌入形式（即将一个字符串表示为一个唯一的整数）。

可能与本文最相关的是 A- 树 [ 24 ] 提出在 B 树页面内使用插值搜索。 然而，学习索引更进一步，并建议使用学习模型替换整个索引结构。

最后，像 Hippo [ 60 ] 这样的稀疏索引都存储有关值范围的信息，但又不利用数据分布的基础属性。

更好的 Hash 函数：类似于基于树的索引结构的工作，在散列图和散列函数方面有很多工作 [ 40,57,56,48] 明确映射到哈希映射内的有限插糟集合的目标。

Bloom-Filters：最后，我们的存在索引直接建立在 Bloom-Filters 的现有工作上 [ 22,11 ] 。 然后，我们的工作通过提出一个 bloom-filter 增强分类模型或者使用模型作为特殊的散列函数，来对问题采取不同的观察方式，这里的优化目标与我们为 Hash Map 创建的散列模型完全不同。

简洁数据结构：在学习索引和简洁数据结构之间存在着一个有趣的联系，特别是诸如小波树的排序选择字典 [ 31,30 ] 。 然而，许多简洁的数据结构集中于 H0 熵（即，对索引中的每个元素进行编码所需的位数），而学习的索引尝试学习基础数据分布以预测每个元素的位置。 因此，学习的索引可能实现更高的压缩率，因为 H0 熵可能以较慢的操作为代价。 此外，对于每个用例，通常都必须仔细构造简洁的数据结构，而学习的索引通过机器学习“自动化”这一过程。 然而，简洁数据结构可能为进一步研究学习指标提供了一个框架。

CDF 建模：我们的范围和点索引模型都与累积分布函数（CDF）的模型密切相关。 CDF 计算是个非平庸的问题，并且已经在机器学习社区 [ 41 ] 。 然而，大多数研究集中在对概率分布函数（PDF）进行建模，留下许多关于如何有效建模 CDF 的开放式问题。

专家混合体：我们的 RM-I 体系结构跟随了一系列有关为数据子集建立专家的研究 [ 42 ] 。 正如我们在我们的配置中看到的那样，它很好地让我们能够解耦模型大小和模型计算，从而实现更复杂的模型，让这些模型的执行起来没那么昂贵。

7 结论和未来工作

我们表明，学习索引可以通过利用索引数据的分布特性来提供明显的好处。 这为许多有趣的研究问题打开了大门。

多维索引：可以说，学习索引理念最令人兴奋的研究方向是将其扩展到多维索引结构。 模型，特别是神经网络，非常擅长捕捉复杂的高维关系。理想情况下，这个模型能够估计任何属性组合过滤的所有记录的位置。

超越索引：学习算法也许令人惊讶的是，CDF 模型也有加速排序和 join 的潜力，而不仅仅是索引。 例如，加速排序的基本思想是使用现有的 CDF 模型 F 将记录大致按排序顺序排列，然后修正几乎完美排序的数据，例如使用插入排序。

GPU / TPU 最后，正如在本文中多次提到的那样，GPU / TPU 将使学习索引的思想更加可行。 同时，GPU / TPU 也有其最大的挑战，最重要的是高调用延迟。 虽然可以合理地假设，由于前面所示的异常压缩比，所有已学习的索引可能适用于 GPU / TPU，但仍需要 2-3 微秒才能对其进行任何操作。 同时，机器学习加速器与 CPU 的集成越来越好 [ 6,4 ]，并且使用批处理请求等技术可以分摊调用成本，因此我们不相信调用延迟是一个真正的障碍。

总之，我们已经证明，机器学习模型有可能比最先进的数据库索引提供显着的优势，并且我们相信这个方向将在未来结出美妙研究成果。

作者介绍：

难易，华为资深工程师，zlog 日志函数库作者，网易 PaaS 第一批开发者。从 2014 年开始设计研发容器集群和产品，聚焦云计算和 PaaS 领域。

参考文章

1. Google’s sparsehash. https://github.com/sparsehash/sparsehash-c11 .
2. Google’s sparsehash documentation. https://github.com/sparsehash/sparsehash/blob/master/src/sparsehash/sparse_hash_map .
3. An in-depth look at googles first tensor processing unit (tpu). https://cloud.google.com/blog/big-data/2017/05/an-in-depth-look-at-googles-first-tensor-proc essing-unit-tpu.
4. Intel Xeon Phi. https://www.intel.com/content/www/us/en/products/processors/xeon-phi/xeon-phi-processors.html .
5. Moore Law is Dead but GPU will get 1000X faster by 2025. https://www.nextbigfuture.com/2017/06/moore-law-is-dead-but-gpu-will-get-1000x-faster-by-2025.html .
6. NVIDIA NVLink High-Speed Interconnect. http://www.nvidia.com/object/nvlink.html .
7. NVIDIA TESLA V100. https://www.nvidia.com/en-us/data-center/tesla-v100/ .
8. Trying to speed up binary search. http://databasearchitects.blogspot.com/2015/09/trying-to-speed-up-binary-search.html .
9. M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M.Isard, et al. Tensorflow: A system for large-scale machine learning. In OSDI, volume 16, pages 265–283, 2016.
10. S. Abu-Nimeh, D. Nappa, X. Wang, and S. Nair. A comparison of machine learning techniques for phishing detection. In Proceedings of the anti-phishing working groups 2nd annual eCrime researchers summit, pages 60–69. ACM, 2007.
11. K. Alexiou, D. Kossmann, and P.-A. Larson. Adaptive range filters for cold data: Avoiding trips to siberia. Proc. VLDB Endow., 6(14):1714–1725, Sept. 2013.
12. M. Athanassoulis and A. Ailamaki. BF-tree: Approximate Tree Indexing. In VLDB, pages 1881–1892, 2014.
13. R. B. Basnet, S. Mukkamala, and A. H. Sung. Detection of phishing attacks: A machine learning approach. Soft Computing Applications in Industry, 226:373–383, 2008.
14. R. Bayer. Symmetric binary b-trees: Data structure and maintenance algorithms. Acta Inf., 1(4):290–306, Dec. 1972.
15. R. Bayer and E. McCreight. Organization and maintenance of large ordered indices. In Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control, SIGFIDET ’70, pages 107–141, New York, NY, USA, 1970. ACM.
16. M. Böhm, B. Schlegel, P. B. Volk, U. Fischer, D. Habich, and W. Lehner. Efficient in-memory indexing with generalized prefix trees. In Datenbanksysteme für Business, Technologie und Web (BTW), 14. Fachtagung des GI-Fachbereichs ”Datenbanken und Informationssysteme” (DBIS), 2.-4.3.2011 in Kaiserslautern, Germany, pages 227–246, 2011.
17. J. Boyar and K. S. Larsen. Efficient rebalancing of chromatic search trees. Journal of Computer and System Sciences, 49(3):667 – 682, 1994. 30th IEEE Conference on Foundations of Computer Science.
18. F. Chang, J. Dean, S. Ghemawat, W. C. Hsieh, D. A. Wallach, M. Burrows, T. Chandra, A. Fikes, and R. Gruber. Bigtable: A distributed storage system for structured data (awarded best paper!). In 7th Symposium on Operating Systems Design and Implementation (OSDI ’06), November 6-8, Seattle, WA, USA, pages 205–218, 2006.
19. K. Cho, B. van Merrienboer, Ç. Gülçehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, EMNLP 2014, October 25-29, 2014, Doha, Qatar, A meeting of SIGDAT, a Special Interest Group of the ACL, pages 1724–1734, 2014.
20. J. G. Cleary. Compact hash tables using bidirectional linear probing. IEEE Trans. Computers, 33(9):828–834, 1984.
21. A. Crotty, A. Galakatos, K. Dursun, T. Kraska, C. Binnig, U. Çetintemel, and S. Zdonik. An architecture for compiling udf-centric workflows. PVLDB, 8(12):1466–1477,2015.
22. B. Fan, D. G. Andersen, M. Kaminsky, and M. D. Mitzenmacher. Cuckoo filter: Practically better than bloom. In Proceedings of the 10th ACM International on Conference on Emerging Networking Experiments and Technologies, CoNEXT ’14, pages 75–88, New York, NY, USA, 2014. ACM.
23. E. Fredkin. Trie memory. Commun. ACM, 3(9):490–499, Sept. 1960.
24. A. Galakatos, M. Markovitch, C. Binnig, R. Fonseca, and T. Kraska. A-tree: A bounded approximate index structure. under submission, 2017.
25. J. Goldstein, R. Ramakrishnan, and U. Shaft. Compressing Relations and Indexes. In ICDE, pages 370–379, 1998.
26. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. Generative adversarial nets. In Advances in neural information processing systems, pages 2672–2680, 2014.
27. G. Graefe. B-tree indexes, interpolation search, and skew. In Proceedings of the 2Nd International Workshop on Data Management on New Hardware, DaMoN ’06, New York, NY, USA, 2006. ACM.
28. G. Graefe and P. A. Larson. B-tree indexes and CPU caches. In Proceedings 17th International Conference on Data Engineering, pages 349–358, 2001.
29. A. Graves. Generating sequences with recurrent neural networks. arXiv preprint arXiv:1308.0850, 2013.
30. R. Grossi, A. Gupta, and J. S. Vitter. High-order entropy-compressed text indexes. In Proceedings of the Fourteenth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’03, pages 841–850, Philadelphia, PA, USA, 2003. Society for Industrial and Applied Mathematics.
31. R. Grossi and G. Ottaviano. The wavelet trie: Maintaining an indexed sequence of strings in compressed space. In Proceedings of the 31st ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, PODS ’12, pages 203–214, New York, NY, USA, 2012. ACM.
32. J. Guo and J. Li. CNN based hashing for image retrieval. CoRR, abs/1509.01354, 2015.
33. G. E. Hinton, O. Vinyals, and J. Dean. Distilling the knowledge in a neural network. CoRR,abs/1503.02531, 2015.
34. J. C. Huang and B. J. Frey. Cumulative distribution networks and the derivative-sum-product algorithm: Models and inference for cumulative distribution functions on graphs. J. Mach. Learn. Res., 12:301–348, Feb. 2011.
35. K. Kaczmarski. B + -Tree Optimized for GPGPU.
36. C. Kim, J. Chhugani, N. Satish, E. Sedlar, A. D. Nguyen, T. Kaldewey, V. W. Lee, S. A. Brandt, and P. Dubey. Fast: Fast architecture sensitive tree search on modern cpus and gpus. In Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data, SIGMOD ’10, pages 339–350, New York, NY, USA, 2010. ACM.
37. T. Kissinger, B. Schlegel, D. Habich, and W. Lehner. Kiss-tree: Smart latch-free in-memory indexing on modern architectures. In Proceedings of the Eighth International Workshop on Data Management on New Hardware, DaMoN ’12, pages 16–23, New York, NY, USA, 2012. ACM.
38. T. J. Lehman and M. J. Carey. A study of index structures for main memory database management systems. In Proceedings of the 12th International Conference on Very Large Data Bases, VLDB ’86, pages 294–303, San Francisco, CA, USA, 1986. Morgan Kaufmann Publishers Inc.
39. V. Leis, A. Kemper, and T. Neumann. The adaptive radix tree: Artful indexing for main-memory databases. In Proceedings of the 2013 IEEE International Conference on Data Engineering (ICDE 2013), ICDE ’13, pages 38–49, Washington, DC, USA, 2013. IEEE Computer Society.
40. W. Litwin. Readings in database systems. chapter Linear Hashing: A New Tool for File and Table Addressing., pages 570–581. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 1988.
41. M. Magdon-Ismail and A. F. Atiya. Neural networks for density estimation. In M. J. Kearns, S.A. Solla, and D. A. Cohn, editors, Advances in Neural Information Processing Systems 11, pages 522–528. MIT Press, 1999.
42. D. J. Miller and H. S. Uyar. A mixture of experts classifier with learning based on both labelled and unlabelled data. In Advances in Neural Information Processing Systems 9, NIPS, Denver, CO, USA, December 2-5, 1996, pages 571–577, 1996.
43. M. Mitzenmacher. Compressed bloom filters. In Proceedings of the Twentieth Annual ACM Symposium on Principles of Distributed Computing, PODC 2001, Newport, Rhode Island, USA, August 26-29, 2001, pages 144–150, 2001.
44. G. Moerkotte. Small Materialized Aggregates: A Light Weight Index Structure for Data Warehousing. In VLDB, pages 476–487, 1998.
45. T. Neumann and G. Weikum. RDF-3X: A RISC-style Engine for RDF. Proc. VLDB Endow., pages 647–659, 2008.
46. OpenStreetMap database ©OpenStreetMap contributors. https://aws.amazon.com/public-datasets/osm .
47. J. Rao and K. A. Ross. Making b± trees cache conscious in main memory. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, SIGMOD ’00, pages 475–486, New York, NY, USA, 2000. ACM.
48. S. Richter, V. Alvarez, and J. Dittrich. A seven-dimensional analysis of hashing methods and its implications on query processing. Proc. VLDB Endow., 9(3):96–107, Nov. 2015.
49. D. G. Severance and G. M. Lohman. Differential files: Their application to the maintenance of large data bases. In Proceedings of the 1976 ACM SIGMOD International Conference on Management of Data, SIGMOD ’76, pages 43–43, New York, NY, USA, 1976. ACM.
50. A. Shahvarani and H.-A. Jacobsen. A hybrid b±tree as solution for in-memory indexing on cpu-gpu heterogeneous computing platforms. In Proceedings of the 2016 International Conference on Management of Data, SIGMOD ’16, pages 1523–1538, New York, NY, USA, 2016. ACM.
51. N. Shazeer, A. Mirhoseini, K. Maziarz, A. Davis, Q. Le, G. Hinton, and J. Dean. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538, 2017.
52. E. R. Sparks, A. Talwalkar, D. Haas, M. J. Franklin, M. I. Jordan, and T. Kraska. Automating model search for large scale machine learning. In Proceedings of the Sixth ACM Symposium on Cloud Computing, SoCC 2015, Kohala Coast, Hawaii, USA, August 27-29, 2015, pages 368–380, 2015.
53. M. Stonebraker and L. A. Rowe. The Design of POSTGRES. In SIGMOD, pages 340–355, 1986.
54. I. Sutskever, O. Vinyals, and Q. V. Le. Sequence to sequence learning with neural networks. In Advances in neural information processing systems, pages 3104–3112, 2014.
55. M. Turcanik and M. Javurek. Hash function generation by neural network. In 2016 New Trends in Signal Processing (NTSP), pages 1–5, Oct 2016.
56. J. Wang, W. Liu, S. Kumar, and S. F. Chang. Learning to hash for indexing big data;a survey. Proceedings of the IEEE, 104(1):34–57, Jan 2016.
57. J. Wang, H. T. Shen, J. Song, and J. Ji. Hashing for similarity search: A survey. CoRR, abs/1408.2927, 2014.
58. K. Weinberger, A. Dasgupta, J. Langford, A. Smola, and J. Attenberg. Feature hashing for large scale multitask learning. In Proceedings of the 26th Annual Internatio nal Conference on Machine Learning, ICML ’09, pages 1113–1120, New York, NY, USA, 2009. ACM.
59. Y. Wu, M. Schuster, Z. Chen, Q. V. Le, M. Norouzi, W. Macherey, M. Krikun, Y. Cao, Q. Gao, K. Macherey, et al. Google’s neural machine translation system: Bridging t he gap between human and machine translation. arXiv preprint arXiv:1609.08144, 2016.
60. J. Yu and M. Sarwat. Two Birds, One Stone: A Fast, Yet Lightweight, Indexing Scheme for Modern Database Systems. In VLDB, pages 385–396, 2016.
61. H. Zhang, D. G. Andersen, A. Pavlo, M. Kaminsky, L. Ma, and R. Shen. Reducing the storage overhead of main-memory OLTP databases with hybrid indexes. In Proceedings of the 2016 International Conference on Management of Data, SIGMOD Conference 2016, San Francisco, CA, USA, June 26 - July 01, 2016, pages 1567–1581, 2016.