拜占庭将军问题与区块链

摘要

在区块链中，不同节点为了达成数据一致而按照同一套逻辑处理数据。但有时候，区块链节点可能为了自身利益而发送错误的信息，也有可能因为网络中断而无法传递接收信息，这就使区块链网络中的节点得到不一致的结果，从而破坏系统一致性。拜占庭将军问题被认为是在分布式系统中达成共识的最难解的问题之一，而与之对应的拜占庭容错共识算法是区块链网络的基础设施之一。

1982 年，图灵奖获得者莱斯利 · 兰伯特（Leslie Lamport）发表了一篇重要的论文《拜占庭将军问题》（The Byzantine Generals Problem），由此展开了长达几十年的、关于如何在分布式系统中有节点被故意破坏的情况下达成共识的讨论。

随着区块链技术的出现，这种讨论有愈演愈烈的趋势。但对大多数人来说，直接去啃论文，无异于望梅止渴，并不能很好地理解论文中要表达的思想。在这篇文章里，我就带你通俗地学习拜占庭将军问题背后的共识协议。

两个将军问题

首先我们来看一个比较简单的例子，我们姑且就称之为“两个将军问题”吧，情形是这样的：

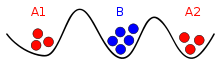
有两支军队一起攻打一座城市，他们各自由一名将军领导。两支军队各自占领城市附近两个不同的山谷。两军之间隔着一个山谷，双方间唯一的通信方式就是派遣信使来往于三个山谷。不幸的是，中间山谷已被城市保卫军占领，也就意味着：信使在通过山谷时可能会被捕。

现在两支军队要协商进攻城市的时间，因为只有两支军队一起进攻才能获得战斗的胜利。所以他们就必须沟通一个时间点来发起进攻，并同意就在那时发动攻击。大家可以想一想，两位将军能就何时进攻达成一致么？

A1 和 A2 军队需要协调，但是他们派出的信使有可能被 B 军队拦截

现在，我来展开介绍这个过程。

1. A1 将军写了封进攻信“我们两支军队凌晨四点一起发动总攻”，并将信交给信使。信使将信带出去后，A1 将军根本不知道信使是被捕了还是已将信送达。因此，A1 将军会犹豫是否发动进攻，除非收到了 A2 将军的确认回信。
2. 假设信使通过了山谷，将信交给了 A2 将军，A2 将军写了封回信“我同意在凌晨四点发动总攻”，他将回信交给信使之后，A2 将军也不知道信使是否成功将回信交给了 A1 将军。因此，A2 将军会犹豫是否发动进攻，除非收到了 A1 将军的确认回信。
3. 假设信使又成功地通过了封锁，将 A2 将军的确认进攻回信交给了 A1 将军。为了让 A2 将军放心，A1 将军还得给 A2 将军写封信“我已经收到了你的确认，我们会取得胜利的”。但是，如果这次的信使被捕了呢？是否 A2 将军还得给 A1 将军发信“我确认我已经收到了你的确认消息”？
4. …

于是，你会发现两位将军陷入了僵局，因为他们不能确认信使是否将信息传递给了对方。因此，这个问题是无解的。

无限次重试，永远不可能达成共识

还有另外一个例子，是说三个人在不同房间，进行投票的故事。三个人彼此可以通过电话进行沟通，但经常会有人不接电话。比如某个时候，A 投票“赞成”，B 投票“反对”，但是 C 不接电话。A 和 B 永远无法在有限时间内获知最终的结果。如果可以重新投票，类似情形也同样会再次发生。

这背后其实有一个很著名的定理：“FLP 不可能性”，它是指在分布式异步通信中，没有任何算法能保证一致性。

我们可能会觉得不可思议，因为在现在的软件系统架构中，分布式架构随处可见，比如 Paxos 算法。这里的区别在于 FLP 定理是学术定理，是遵循严格数学证明的，考虑的是最极端的情况，而 Paxos 算法是工程实践，学术上的极端性一般情况下很少发生，即便发生，多试几次可能就成功了。

正如第一个例子所示，不可能每次派出的信使都被 B 军队拦截，所以 A1、A2 将军可以一次性派出 100 个信使，只要有 1 个信使通过了封锁，就算是送信成功。而同样在投票的例子里，ABC 每轮都给彼此打多次电话，直至打通，这样也能达成共识。

有句话是这么说的：科学告诉你什么是不可能的；工程则告诉你，付出一些代价，我可以把它变成可能。这就是工程的魅力。我很赞同。

拜占庭将军问题

接下来，我们来看拜占庭将军问题，它相较于两将军问题要复杂得多。莱斯利·兰伯特在他的论文里是这么描述这个问题的：

9 位拜占庭将军分别率领一支军队要共同围困一座城市，因为这座城市很强大，如果不协调统一将军们的行动策略，部分军队进攻、部分军队撤退会造成围困失败，因此各位将军必须通过投票来达成一致策略，要么一起进攻，要么一起撤退。

因为各位将军分别占据城市的一角，他们只能通过信使互相联系。在协调过程中每位将军都将自己投票“进攻”还是“撤退”的消息通过信使分别通知其他所有将军，这样一来每位将军根据自己的投票和其他将军送过来的投票，就可以知道投票结果，从而决定是进攻还是撤退。

而问题的复杂性就在于：将军中可能出现叛徒，他们不仅可以投票给错误的决策，还可能会选择性地发送投票。假设 9 位将军中有 1 名叛徒，8 位忠诚的将军中出现了 4 人投“进攻”，4 人投“撤退”，这时候叛徒可能故意给 4 名投“进攻”的将军投“进攻”，而给另外 4 名投“撤退”的将军投“撤退”。这样在 4 名投“进攻”的将军看来，投票是 5 人投“进攻”，从而发动进攻；而另外 4 名将军看来是 5 人投“撤退”，从而撤退。这样，一致性就遭到了破坏。

还有一种情况，因为将军之间需要通过信使交流，即便所有的将军都是忠诚的，派出去的信使也可能被敌军截杀，甚至被间谍替换，也就是说将军之间进行交流的信息通道是不能保证可靠性的。所以在没有收到对应将军消息的时候，将军们会默认投一个票，例如“进攻”。

以上就是拜占庭将军问题的简单描述，如果将军们在有叛徒存在的情况下仍然达成了一致，我们就称达到了“拜占庭容错”。那这跟我们在多台计算机中达成共识有什么关系呢？

其实，我们可以这么看这个问题，把将军看做是计算机；信使就是网络；信使被截杀，代表着计算机间的网络不可达；而将军叛变则代表着程序出错。这么一解释，有没有豁然开朗的感觉？

拜占庭将军问题有解吗？答案是有的，但有个前提，那就是叛徒的数量不能大于等于 1/3。

这个值怎么得出来的呢？这里我们可以用最小化模型来探讨，因为共识的基础是要少数服从多数，那么最小化模型的将军数是 3。假设有 3 个将军 A、B、C，假设三人中有一个是叛徒。

• 当 A 发出“进攻”命令时，B 如果是叛徒，他可能告诉 C，他收到的是“撤退”的命令。这时 C 收到一个“进攻”，一个“撤退“，于是 C 无法判断真实命令。
• 如果 A 是叛徒，他告诉 B“进攻”，告诉 C“撤退”。当 C 告诉 B，他收到“撤退”命令时，B 由于收到了 A“进攻”的命令，而无法与 C 保持一致。

正由于上述原因，只要有一个是叛徒，即叛徒数等于 1/3，拜占庭问题便不可解。

既然有解，我们就来看看有哪些解法。

1. 口头协定

所谓口头协定，就是将军们使用信使传递口头信息，要满足以下三个条件：

• 被发送的消息能够被信使正确传递；
• 接受者知道消息是哪个将军发的；
• 能够知道谁没有发送消息。

也就是说，信道可信，消息来源可知。消息传递一般的步骤如下：

1. 每位将军都给其他将军传递口信；
2. 每位将军将自己收到的口信分别转给其他将军；
3. 每位将军根据收到的口信做出决策。

如此来看，每轮下来，每个将军都会收到 N（将军数）条消息，相当于每个将军都知道了其他将军手里的投票，如果有一半以上的将军说“进攻”，那么就可以进攻。即便是有叛徒，只要听大部分人的，就可以保证达成一致。

但是口头协定有个很大的弊端，就是不知道消息的上一个来源是哪个将军发出来的，就算将军中间有叛徒，也不能知道谁是叛徒。

2. 书面协定

不同于口头协定的将军间使用口信传递信息，而是使用书信，并且在书信上都要签上国王发给将军们的印章，相比于口头协定，又多了两个隐含条件：

• 将军使用印章对书信签名，签名确定将军身份，不可伪造，篡改签名可被发现；
• 任何将军都可以验证签名的有效性。

书面协定的本质就是引入了“签名系统”，这使得所有消息都可追本溯源。只要采用了书面协定，忠诚的将军就可以达到一致。现在这种方式下，将军们按照以下方式发送消息：

1. 每位将军分别给其他将军发送书信，并在书信上附上自己的签名；
2. 其他将军收到书信后，附上自己的签名后再发给所有其他将军；
3. 每位将军根据自己收到的书信进行决断。

书面协定貌似完美解决了拜占庭将军问题，但是不得不说实际上的解决是建立在诸多限制条件下的。在现实的分布式系统中，我们可能会遇到各种各样的问题。例如：

• 没有考虑信使传递消息的时延问题；
• 真正可信的签名体系很难实现，也很难避免签名造假；
• 将军们的印章是国王颁发的，难以褪去中心化机构的影响。

另外，如果每个将军都向其他将军派遣信使表达自己的观点，那么一轮信息交流需要 90 次的信使往来。而且每个将军的观点都可能不一致，在异步通信模式下，几乎很难达成一致。而且让所有将军都相信中心化的国王签发的印章的真实性，实际上也违反了整个问题的前提，那就是将军们互相不信任，即便是有国王的存在。

区块链

不难看到，以上两种解法或多或少都有些瑕疵，不难完美的解决问题。那么有没有一种趋近完美的解决方案呢？当然是有的，那就是中本聪在创造比特币的时候提出的区块链技术。

拜占庭将军问题之所以难解，一个重要的原因就是在任意时间，系统中可能会存在多个提案，也就是问题描述中的每个将军都可以给出自己的意见。这样一来，很难在一个时刻对结果进行一致性确认。中本聪创新性地引入 PoW 共识算法，解决了两个困难。

1. 限制一段时间内提案的个数，只有拥有对应权限的节点（将军）可以发起提案。在比特币里，是通过随机哈希计算分配权限的，谁第一个计算出对应的答案，谁才有权限发起提案。
2. 由强一致性放宽至最终一致性。对应一次提案的结果不需要全部的节点马上跟进，只需要在节点能搜寻到的全网络中的所有链条中，选取最长的链条进行后续拓展就可以。

同时，区块链技术使用非对称加密算法对节点间的消息传递提供签名技术支持，每个节点（将军）都有属于自己的秘钥（公钥私钥），唯一标识节点身份。使用非对称加密算法传递消息，能够保证消息传递的私密性，而且消息签名不可抵赖，不可篡改。

使用公钥加密的数据，使用公钥对应的私钥进行解密；使用私钥进行签名的消息，只需要使用私钥对应的公钥验证签名即可。比如，A 将军想要给 B 将军发送消息，那么只需要使用 B 将军的公钥加密消息，B 将军收到消息后使用自己的私钥解密消息即可。而如果 A 将军想申明自己的身份，只需要将消息使用自己的私钥进行签名即可，B 将军收到消息后就可以使用 A 将军的公钥验证消息的来源。这样就将一个不信任的网络变成了信任网络。

在对区块链的研究中，经常听到有人说 PoW 算法浪费了大量的电力资源、GPU 资源等，是不可取的做法。我认为区块链使用 PoW 共识算法来保证系统的去中心化，成就可信网络，凡事都是有得有失，达成信任这一目标不管以何种方式完成，成本永远不可能为零。而在以比特币为首的区块链网络中，电力资源、GPU 资源等就是达成信任需要付出的成本。

在区块链这样的分布式网络中，我们还是以将军为例：

• 每位将军都保留一份历史消息账本；
• 因为每份消息都是进行过签名的，所以如果有背叛的将军，我们很容易就能找出来；
• 在一轮共识的流程里，即便有消息不一致，但是只要背叛将军个数不超过 1/3，这一轮共识就能达成。

这里，我们很清楚地知道，区块链和拜占庭将军问题的共性所在了，都是决定由谁发起消息（提案），以及如何在分布式系统中达成一致的问题。

总结

由多门技术糅合在一起的区块链技术，它摒弃了口头协定与书面协定的诸多问题，使用非对称加密算法、PoW 等共识算法，构建了一套分布式系统中大家都准守的协议，至善至美的解决了拜占庭将军问题。同时也为未来的世界提供了无限的可能性，正所谓：未来可期，未来以来。

参考列表

1. Leslie Lamport: 《 The Byzantine Generals Problem 》 1982
2. E. A. Akkoyunlu、K. Ekanadham & R. V. Huber 《 Two Generals Problem 》1975
3. 杨宝华：《区块链技术指南》 2017
4. 中本聪：《 Bitcoin: A Peer-to-Peer Electronic Cash System 》2008

作者介绍：自游，区块链底层架构师。16 年初接触区块链并全职投入，现供职于某世界 500 强企业做区块链底层研究及 BAAS 平台搭建。精通区块链底层存储、共识等技术，职业方向偏重联盟链体系。

区块链现在还处于超级早期的阶段，泡沫一定有，而且还很大，但如美图 CEO 蔡文胜所说：“区块链是人类有历史以来最大的泡沫，但泡沫才刚刚开始，只能拥抱泡沫，不参与才是最大的风险。”如何了解和参与区块链？我们推出了“区块链前哨”这个公众号，面向区块链兴趣爱好者、开发者，提供最新最热区块链资讯，深度分析区块链技术及应用、展示国内外创新实践案例。

“时代抛弃你时，连声再见都不会跟你说。”未来已来，让我们一起拥抱区块链，拥抱未来。欢迎扫码关注！