关键要点
- 远距传动是最先被描述的量子信息处理过程之一。它使用纠缠在瞬间远距离传输信息,但它不能用于传送大型物体,如人或猫。
- 一旦人们意识到量子系统的计算复杂性实际上是一种计算能力,那么量子信息理论就真正起飞了。它可以被应用于其他问题上,例如在公钥密码学中用到的因子分解。
- Shor 的对数算法并没有破坏密码学,“量子安全”加密协议已经在开发当中。
- Shor 的算法是第一个量子“杀手级应用”。两年后,出现了第二个,也就是 Grover 的搜索算法。Grover 算法可以在 O(n) 时间内搜索未排序的数据库。
- 在过去几年中,随着量子计算和机器学习逐渐升温,人们很自然会想是否可以把它们结合起来。到目前为止,答案似乎是肯定的。
为了理解为什么量子计算机会如此有趣,有必要简要地挖掘一下复杂性理论。虽然它看起来与我们大多数人日常工作相去甚远,但复杂性理论不只是出现在大学课堂或求职面试的白板上。量子计算之所以这么快,并不是因为量子计算机的处理速度(其实它的速度很慢)或计算机的内存速度(对速度影响微乎其微),而是因为它的算法。量子计算机的新算法具有与经典等价算法完全不同的复杂性特征。
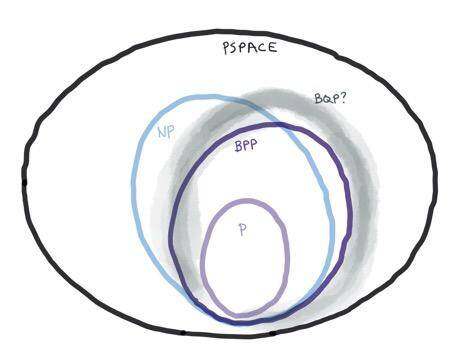
研究复杂性的人将问题按照复杂性进行分类。一个给定的问题可能属于多个类,并且有很多复杂的类,因此,有时候也将其称为复杂性动物园。所幸的是,我们只需要了解少数几个。顾名思义,NP-hard 问题就是指难以解决的问题。随着解决方案中元素(数字、点或城市)数量的增加,它们会变得更加难以解决。NP-complete 问题是一类NP-hard 问题,其解决方案可以推广到解决任何其他NP-hard 问题。NP-complete 问题的有效算法正是复杂性理论的终极解决方案(但量子计算不提供这个解决方案)。
复杂性类不仅通过大O 符号来定义,一般来说,NP-hard 问题用事物的数量进行多项式缩放——也就是说,它们在2 的O(log(n)) 次方时间内是可解的。这意味着,计算3 个点需要8 秒(这是合理的),计算10 个点需要17 分钟(已经不是很合理了),计算20 个点需要12 天(有点荒谬),计算40 个点需要35,000 年(逆天了)。或者换句话说,硬件在计算完成26 个点计算之前就已经过时了,对于31 个点的计算,任何编写程序的人很可能在得到答案之前就已经死了。
重要的量子算法
运距传动
虽然运距传动不是一种计算,但如果少了它,对量子信息的讨论就是不完整的。运距传动是最先被描述的量子信息处理过程之一。它使用纠缠在瞬间远距离传输信息,但它不能用于传输大型物体,如人或猫。它仅适用于单个粒子,甚至不传输实际粒子,只传输有关其状态的信息。它可以传输粒子的全量子位丰富(full qubit-rich) 状态,这让关心量子态的人感到非常兴奋。量子信息不能通过经典的信道传输,因为量子态的任何经典测量都会破坏它(“失稳”)。
量子信息无法被复制(“无克隆”定理),因此传送粒子信息会破坏原始粒子的状态,这可能是“远距传动”这个名称的灵感来源。物质无法在一个地方解体而在另一个地方再生,但信息可以。
爱因斯坦的狭义相对论认为,信息的传播速度不如光速快。远距传动实际上并没有违反这一理论,它只是看起来违反罢了。为了纠缠,光子对必须在同一个地方开始,然后远离彼此。这意味着“潜伏”信息的传播速度比光速慢,因此仍然遵循爱因斯坦的理论。这有点像信鸽之间的通信,虽然鸽子可以比骑马的人更快地运送便条,但是马必须先将鸽子运送到目的地,这样鸽子才能带着便条飞回家。为了传送有用的信息(而不仅仅是概率测量的结果),远距传动协议还需要经典的通信手段——也就是说,除了一匹马先把信鸽送到目的地,还需要第二匹马跟着信鸽回去,这匹马带有如何阅读信鸽腿上便条的指示。这意味着量子远距传动不太可能在不久的将来用于高频交易。然而,它仍然是在不失稳的情况下传输完整量子态最有效的方式。
量子系统的模拟
量子系统(如量子计算机)可用于模拟另一个量子系统,这并不令人感到惊讶。令人感到惊讶的是,经典计算机在模拟量子系统方面表现得非常糟糕。模拟小型量子系统倒还好,但要模拟大型量子系统实际上是不可能的。量子态信息的丰富性意味着,随着元素数量的增长,模拟所需要做出的工作量呈指数级增长。Richard Feynman 是第一个注意到量子系统具有高度计算复杂性的人,这为量子信息理论的后期发展奠定了基础。
因子分解
一旦人们注意到量子系统的计算复杂性实际上是计算能力,量子信息理论才真正起飞。我们可以将其应用于其他问题上。因子分解是指找出乘积等于一个给定数字的两个数。因子分解有时候会很有用,但最有趣的是,它太难了,而且是非常之难。因子分解是单向函数的一个例子,如果两个除数都是已知的,那么找到它们的乘积就很容易,但从乘积中找到除数可能需要很长的时间。最大的一个已被分解的数字是一个 232 位的数字,但实际上它并不算很大(作为对比,pi 已被计算到了至少五万亿个数字)。但分解一个 232 位的数字已经算得上是一个重大项目了,它使用了数百台机器,研究人员花了两年时间才找到除数。
这种不对称的难度使得因子分解被用在了公钥加密(例如 RSA)中。两个素数的乘积用于生成公钥,发送者使用该公钥来加密消息。然后,接收方基于其中一个原始因数使用私钥来解密消息。如果一个人知道原始的除数,那么解谜就很容易,否则的话,那将会是一个很棘手的问题。
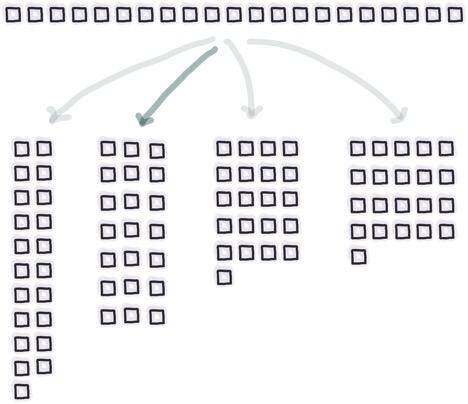
虽然它没有经过数学证明,但人们普遍认为,一般性因子分解的难度规模比多项式大,但比指数小。这被称为亚指数,用 2 的 O(n) 次方表示。实际上,如果数字足够大,基本上是无法通过经典方法来分解的。
1994 年,数学家 Peter Shor 证明可以使用量子计算机在多项式时间内解决因子分解问题。他听过关于量子计算理论前景的讨论,但当时没有人发现任何有用的算法。他开始考虑如何使用量子计算机解决一般的计算问题,但没有告诉任何人他在做什么。他花了一年的时间(兼职)提出了用于寻找对数的量子算法。四天后,他将对数算法用在了因子分解上。
因为因子分解是大多数公钥加密的核心部分,所以Shor 的研究成果引起了人们的注意。不过,Shor 的算法并没有破坏密码学,“量子安全”加密协议已经在开发当中。此外,我们将在本系列文章的第3 部分中看到,我们需要一台具有数千个量子位的量子计算机才能成功运行Shor 算法。
Shor 的算法通过使用量子叠加来尝试各种可能性。
然而,Shor 算法的细节比仅仅“尝试所有可能的因素并找出正确的那个”更加复杂。虽然这可以在量子计算机上完成,但任何测量都会产生随机——并且很可能是不正确的——因素。
Shor 算法的聪明之处在于,在尝试了很多可能性之后,它会将所有答案干扰在一起,因此测量更有可能产生正确的答案而不是错误的答案。对于经典计算机来说,“干扰答案”并不合理,但量子计算机利用量子态的波动特性却可以做到这一点。干扰获得正确结果的可能性是许多量子算法的共同特征。
Shor 解决方案的第一部分是进行经典计算,将因子分解问题变成查找函数周期(即它的频率)的问题。一旦完成了这一步,问题就与波和频率有关,那么就有可能使用量子波和干扰的解决方案。
在经典数学中,傅里叶变换用于将函数(如波信号)转换为组成频率。为了找到未知函数的傅立叶变换,有必要在许多点上进行测量,以便计算出它重复的频率。例如,标准正弦波的傅里叶变换是一对尖峰(只有一个频率,围绕 y 轴镜像)。框函数的傅里叶变换是逐渐下降的凹凸。
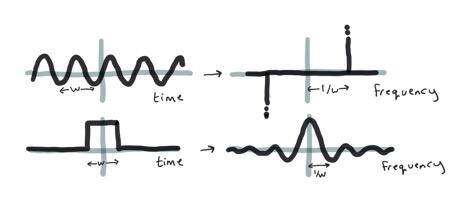
量子傅立叶变换也具有选择构成时间序列的频率的目标,但它能够使用叠加在多个点上及时有效地测量函数,然后对波进行干扰,这样正确的答案就会放大,错误的答案就会消退。完成这一步后,任何测量都很有可能让系统收敛到正确的答案。
将波混合在一起,以便让错误的答案自行消退,这与经典计算机的工作方式非常不同,但这也是我们大多数人在宏观世界中曾经经历过的事情。例如,降噪耳机通过向现有噪声添加额外噪声达到降噪的效果。它们发出额外的声波,试图再现外部噪声,只不过使用了相移。只要新的声波与原先的噪声波相差 180 度,并且是完美的副本,它们将整齐地相互抵消,从而为耳机佩戴者带来安静的世界。
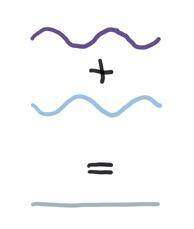
搜索
Shor 的算法是第一个量子“杀手级应用”。两年后,出现了第二个,也就是 Grover 的搜索算法。Grover 算法可以在 O(根号 n) 的时间复杂度搜索未排序的数据库。例如,如果只知道一个人的电话号码,可用它在电话簿中查找姓名。Grover 算法没有像 Shor 的因子分解算法那样提供同样惊人的速度,它是二次加速,而不是指数级加速(也就是说,它按照元素数量的平方根进行缩放)。Grover 算法的速度虽然比较保守,但其适用性却十分广泛。
尽管 Grover 只针对数据库搜索来描述他的算法,但事实上它应该更加通用。被搜索的东西是能够满足某些功能的东西——也就是问题的答案(从技术上讲,目标是“函数的逆”)。例如,问题可能是“我应该用什么密钥来解密这个消息?”换句话说,Grover 的搜索算法可以用来加速密码的暴力破解,即使不是基于因子分解加密的。它还可用于估计一组数字的平均值(平均值或中值)。
像其他很多量子算法一样,Grover 算法是带有概率性的。每次执行都有可能给出正确的答案,并且也有少许的可能性获得错误的答案。这看起来似乎不太令人满意,但实际上它比表面上看起来的更有用处。因为答案是函数的解决方案,所以如果算法给出错误的答案就会非常明显。对于一个包含 n 个元素的系统,使用 O(根号 n) 的时间复杂度寻找解决方案,如果得到错误的答案,将是非常令人沮丧的。不过,即使重复这种长时间的慢速计算多次,总的时间复杂度不变,仍然比使用确定性经典算法快得多(计算错误的概率不随 n 增加,这就是为什么可以容忍误差)。
碰撞
我们可以对 Grover 算法进行一般化,用它来解决“碰撞问题”。也就是说,我们不找可以满足函数的东西,而是尝试找出产生相同答案的多个元素。这对于理解空间中的物理碰撞以及更常见的问题(例如找到两个生日是同一天的人)非常有帮助。与 Grover 的原始算法一样,它可以通过查找具有相同散列值的两个数字来进行加密攻击(它的经典版被称为“生日攻击”)。
旅行推销员问题
量子算法通常会尝试所有可能的解决方案,然后通过幅度放大选择其中正确的一个,因此,量子计算机似乎应该在解决优化问题方面表现出色。到目前为止,还没有通用的量子优化算法,但是对于某些优化问题的子类别,确实存在有吸引力的量子解决方案。最著名的优化问题之一被称为旅行推销员问题,即为在多个地点之间旅行的推销员找到最短路线。随着位置数量的增加,寻找最佳路线的难度也随之增加。旅行推销员问题是 NP-hard 问题,并且其难度随着位置数量的增加呈指数级增长。这个问题的精确解决方案可能需要用很多年(甚至数百万年)才能计算出来,即使只有几十个城市。
旅行推销员问题是一个持续研究的领域。直到最近,最著名的量子算法时间复杂度是 O(根号 n 的阶乘)(二次加速),而最著名的经典算法时间复杂度是 O(2 的 n 次方)。2017 年 3 月,发布了一个最新量子算法,该算法在大多数情况下接近二次加速,并且仍有改进的空间。
机器学习
在过去几年中,随着量子计算和机器学习逐渐升温,人们很自然会想是否可以把它们结合起来。到目前为止,答案似乎是肯定的。在数学层面,量子态计算和机器学习模型都严重依赖矩阵。从概念上讲,机器学习是关于在数据中寻找模式,量子计算的干扰和放大波模型非常适合用于寻找模式。
量子计算机可以使用对数资源进行某种类型的矩阵求逆(矩阵求逆等效于求解线性方程组)。矩阵求逆有助于解决一些机器学习问题。更一般地说,Grover 算法可用于搜索“正确”的答案(即满足给定函数的答案)。其他机器学习问题,例如聚类,可以使用其他独特的量子算法。
理论上已经证明,量子计算机能更好地解决所谓的“黑盒问题”(通过探测发现未知的随机比特序列),研究人员已经演示了如何解决5 个比特的黑盒问题。除了能够(原则上,用足够强大的计算机)能够发现如此长的序列(使用经典计算机可能永远也算不出来),量子计算机对读数中的噪音也更加宽容。
没有通用的量子加速
所有这些算法都是针对特定的问题,其中一些(例如搜索或旅行推销员问题)存在很多潜在的应用场景,但算法本身非常具体。现在还不存在一种已知的“通用量子加速”。换句话说,就复杂性类别而言,已知BQP 与NP 重叠,但目前还不知道重叠的程度。有可能是NP 包含了BQP,但尚未得到证实。 Peter Shor 指出,要让量子算法提供有趣的加速,需要对正确答案的计算路径进行建设性的干涉,并对错误答案的路径进行相互抵消,现在还没有一个通用的过程。考虑到问题的难度如此之大,可能永远不会有。
不过,缺乏通用量子算法不应该对已知算法的有趣程度或适用性产生影响。本系列文章的下一篇将讨论这些问题,并探究量子计算的未来。
关于作者
 Holly Cummins 是一位全栈开发人员和云计算技术主管。她经常发表演讲,是一位 Java Champion,以及 Enterprise OSGi in Action 一书的作者。Holly 拥有牛津大学量子计算博士学位(PhD)。
Holly Cummins 是一位全栈开发人员和云计算技术主管。她经常发表演讲,是一位 Java Champion,以及 Enterprise OSGi in Action 一书的作者。Holly 拥有牛津大学量子计算博士学位(PhD)。
查看英文原文: Cats, Qubits, and Teleportation: The Spooky World of Quantum Computation (Part 2)












评论