无痛的增强学习入门： 增强学习形式化

系列导读：《无痛的增强学习入门》系列文章旨在为大家介绍增强学习相关的入门知识，为大家后续的深入学习打下基础。其中包括增强学习的基本思想，MDP 框架，几种基本的学习算法介绍，以及一些简单的实际案例。

作为机器学习中十分重要的一支，增强学习在这些年取得了十分令人惊喜的成绩，这也使得越来越多的人加入到学习增强学习的队伍当中。增强学习的知识和内容与经典监督学习、非监督学习相比并不容易，而且可解释的小例子比较少，本系列将向各位读者简单介绍其中的基本知识，并以一个小例子贯穿其中。

上一篇我们以蛇棋为例，主要介绍了增强学习的核心流程，那就是 Agent 与 Environment 的交互。

无痛的增强学习入门：基本概念篇

2 增强学习形式化

这一篇我们需要进一步形式化这个过程，站在数学的角度分析这个问题的解决方案。对于增强学习来说，大家一般喜欢以马尔科夫决策过程这样一个模型作为形式化的手段。

2.1 MDP——策略与环境模型

我们再回到蛇棋中来。有哪些因素决定蛇棋最终获得分数的多少？其实就两个：一是选择投掷什么样的手法，二是投掷出的数目。第一个问题是玩家可以决定的，第二个是无法确定的，这里充满了随机性。

如果再进一步看，有哪些结果 / 状态决定了最终的得分呢？那就是每一步走到位置和每一步选择的投掷手法了。比方说上一节展示的游戏过程。我们用表示 t 时刻游戏的状态，也就是行走到的位置，用表示 t 时刻选择的手法，那么游戏过程就可以用一条状态 - 行动链条来表示了：

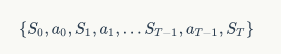
这个链条有两种状态转换的模型，一种是从状态到行动的转换，另一种是从行动到状态的转换，这两种转换分别对应了前面提到的两个决定因素。对于第一种转换来说，它通常被认为是由玩家的策略决定的，对于第二种转换来说，它通常是由环境决定的。下面就来看看详细形式化这两种转换。

所谓的策略，就是根据当前的状态选择“自认为”最好的行动，如果我们认为玩家会对每一个行动进行一次打分，那么玩家最终会选择打分最高的那种行动；如果我们认为玩家的每一个行动都有一定的概率，所有行动的概率总和为 1，那么玩家在特定情况下就会选择概率最高的一种行动，形式化来说，就是选择：

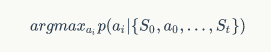
这个公式的结果。可以看到这个条件概率还是比较复杂的，给定的条件比较复杂，我们需要对其做一定的化简。这里可以使用蛇棋中的状态之间无依赖的性质，也就是说，当前选择什么行动只和当前的状态有关，和前面的状态无关。这一点比较容易理解，如果我这一步在“55”，那么我只需要考虑 55 前面有什么情况就好，至于我从“1”如何走到“55”，这些并不需要我们关心，我们的目标十分明确，那就是尽快从“55”移动到“100”，于是上面的公式就变成了。

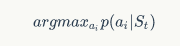
这样问题就得到了简化。对于策略部分，我们要实现一个映射，使得对于每一个状态，我们能找到一个最优的行动方式。

下面一步就是环境了。当完成了行动确定后，这一步要完成真正的状态转移。这里也非常明显，下一步的状态并不受前一步状态影响，于是这里的状态转换就可以定义为：

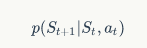
比方说我们在“55”这个位置，我们如果选定“1-3”的骰子，假设骰子投掷结果是“均匀”的，那么接下来我们的棋子将以等概率出现在“56”，“57”，“58”这三个格子中。但是由于梯子的存在，落在这三个格子中的棋子可能会到达其他位置，所以实际当中我们需要考虑每一个格子到所有格子的概率。

了解了这两个过程，我们就可以重新看看 MDP 这个词了。马尔可夫决策过程包含了两层含义，其中的“马尔可夫”表示了状态间的依赖性，下一个状态只和前一个状态产生依赖，并不和更早的状态产生联系；而“决策”表示了其中的策略部分将有玩家决定，而其他部分保持随机性；而“过程”表示了时间的属性，每一轮的操作都将时间向前推进，状态更新，行动产生，然后状态再更新……

了解了这些，我们就来看看代码如何实现吧，下面这个函数展示了由蛇棋类提供的状态转换的表格的代码：

 
def state_transition_table(self):
    table = np.zeros((len(self.dice_ranges), 101, 101))
    ladder_move = np.vectorize(lambda x: self.ladders[x] if x in self.ladders else x)
 
    for i, dice in enumerate(self.dice_ranges):
        prob = 1.0 / dice
        for s in range(1, 100):
            step = np.arange(dice)
            step += s
            step = np.piecewise(step, [step > 100, step <= 100], [lambda x: 200 - x, lambda x: x])
            step = ladder_move(step)
            for final_move in step:
                table[i, s, final_move] += prob
    table[:,100, 100]=1
    return table

2.2 状态与行动的评估

前面介绍了 MDP，其实游戏的关键在于策略，如何行动。每一个行动一定需要一个行动准则，也就是说我们要能够量化某一个状态或者某一个行动的价值，这样才好让玩家做出明智的判断。所以接下来一个重要的工作就是量化这些价值。

幸运的是，模型已经帮助我们完成了最重要的一步——它提供了可以量化的某一时刻的反馈 reward。虽然这和我们最终的目标有些不同，但是我们可以将其扩展使之称为我们的目标。前面我们已经提到，当我们落在非终点的位置上时，reward=-1，当我们落在终点时，reward＝100。于是这部分内容也可以写成代码的形式：

 
def reward_table(self):
   table = np.array([-1] * 101)
   table[100] = 100
   return table

到这里，我们有个状态转移的信息，有了每一步行动后的 reward，可以说，基本的信息已经充足了。那么现在就可以求出我们的最优策略了么？还不行，现在的计算还不够方便。前面提到我们的策略是要将这个公式最大化：

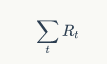
这个公式并不是很容易计算的，如果时间轴是有限的，也就是说我们可以在有限步完成游戏，那么这个公式是可以计算的，但如果游戏有可能无限进行下去呢？比方说每次快到”100"这个位置时，投掷的骰子数目都很大，导致永远无法正好到达“100”这个位置？那么在这种情况下，我们就不能直接用上面的公式了。为了解决这个问题，我们要对降低未来回报对当期的影响，也就是对未来的回报乘以一个打折率。所以修正后的公式变成了：

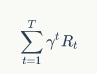
那么这个公式形式和现实有什么对应呢？最直接的对应就是商业银行的储蓄了。我们知道把钱存入银行，银行是可以支付利息的（当然有时也有负利息）。我们假设银行的年利率是 10%（现实中恐怕很难见到），于是我们存入 100 元，一年后它就变成了 110 元。如果我们希望一年后它变成 100 元，那么现在需要存入多少钱呢？大概是 90.9 元，这个数字比 100 元小一些。把这个思想搬过来，对于未来可以获得的某个 Reward，换算到当下是要打折的。这个打折率一般来说是小于 1 的，这样一来长期回报的这个数列的和就变得有限了，只要有限我们就可以计算了。

解决了长期回报的可表示问题，下面一个问题是：能不能用一个数值表示这个公式呢？于是我们需要定义另外一个变量——长期回报（Return）。所谓的长期回报，是将当前状态以后所有的 Reward 全部加起来，得到一个汇总的值。有了这个值，我们就可以衡量每一个策略的价值（Value）了。每一个策略都对应着一种行动，行动过后，对应的 Reward 以及 Return 就能够估计出来，由于不同的行动对应着不用的 Return，每种行动的高下可以进行比较，于是策略间的价值也就可以评估了。

根据 MDP 的模型形式，价值函数可以分为两种类型：

1. 状态价值函数：也就是求出当前状态 s 下按照某种策略的期望 Return。
2. 状态 - 行动价值函数：也就是求出当前状态 s 和行动 a 已知后，按照某种策略的期望 Return。

这两种函数有什么关系么？下面就将这两个函数的形式展现出来。某个状态的价值函数，相当于依从某个策略把所有从这个状态出发的可能路径走一遍，将这些路径的长期回报进行”加权平均“，由于路径是无限的，因此这个过程相当于求期望：

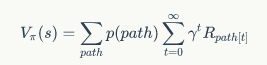
由于增强学习的过程是一个马尔可夫决策过程，于是路径部分可以展开：

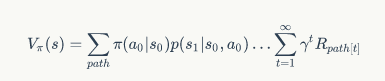
这样的公式形式显然不够优雅，于是我们使用高中时使用的代换消元法，就可以得到：

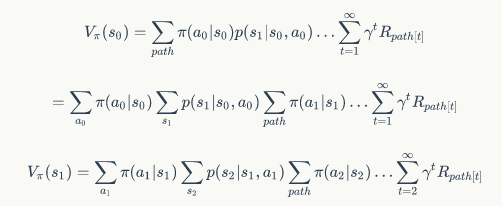
两式相融合，再经过一些变换，可以得到：

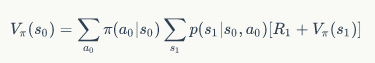
公式中的表示了到达下一状态时获得的 Reward。通过这样的计算，我们发现状态价值函数是可以完成自我计算的。任意一个状态的价值可以由其他状态的价值得到，这个公式就被称为 Bellman 公式，是下面进行策略求解的基础公式之一。之所以被称为”之一“，是因为状态 - 行动价值函数同样有一个类似的公式：

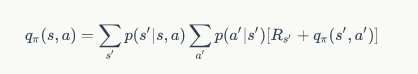
这两个公式可以说是整个增强学习理论的基石，读者务必要对其有深入的了解。

2.3 表格版 Agent

说了这么多，下面回到正题。我们的目标是针对一个问题，找到使其可以实现长期回报最大化的策略。对于蛇棋这样的问题，我们可以采用”做表格“的方式进行计算。所谓的做表格，就是将每一个状态相关的信息都进行单独计算单独考虑，不做汇总归纳。以下是我们的表格版 Agent 的初始化代码：

 
class TableAgent:
   def __init__(self, state_transition_table, reward_table):
       self.table = state_transition_table
       self.reward = reward_table
       self.state_num = self.table.shape[1]
       self.act_num = self.table.shape[0]
       self.policy = np.zeros(self.state_num, dtype=np.int)
       self.value_pi = np.zeros((self.state_num))
       self.value_q = np.zeros((self.state_num, self.act_num))
       self.gamma = 0.8

可以看出，一个 Agent 需要知道以下的信息：

• 蛇棋中的状态转移情况：这是一个三维的数组，也就是存储的结构
• 蛇棋中的 Reward 记录：这是一个一维数组
• 蛇棋的状态数目：100 个
• 蛇棋的行动数目：看个人手法决定（\微笑\微笑）
• 策略：我们会为每一个状态最终选择一个最优行动，如果有两个行动同时最优，那么会任选一个
• 状态价值函数
• 状态 - 行动价值函数
• 打折率

到此为止，初始化就结束了。最后让我们一起明确一下求解最优策略的思路。前面说过，给定某个状态，求解最优策略，相当于求解：

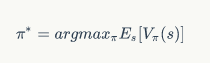
将其中的策略变量摘掉，可以认为，对于任意的状态，求解

也就是说，为了求解行动，我们要先知道价值函数。

而价值函数的定义，在前面已经介绍了，它是在策略确定的时候计算得到的。嗯，听上去好像有点矛盾了……我们把这个问题交给下一节去解决。

作者介绍

冯超，毕业于中国科学院大学，猿辅导研究团队视觉研究负责人，小猿搜题拍照搜题负责人之一。2017 年独立撰写《深度学习轻松学：核心算法与视觉实践》一书（书籍链接： https://item.jd.com/12106435.html ），以轻松幽默的语言深入详细地介绍了深度学习的基本结构，模型优化和参数设置细节，视觉领域应用等内容。自 2016 年起在知乎开设了自己的专栏：《无痛的机器学习》，发表机器学习与深度学习相关文章，收到了不错的反响，并被多家媒体转载。曾多次参与社区技术分享活动。