从赌钱游戏看 PageRank 算法

谈到并行计算应用，会有人想到 PageRank 算法，我们有成千上万的网页分析链接关系确定排名先后，借助并行计算完成是一个很好的场景。长期以来，Google 的创始发明 PageRank 算法吸引了很多人学习研究，据说当年 Google 创始者兴奋的找到 Yahoo! 公司，说他们找到一种更好的搜索引擎算法，但是被 Yahoo! 公司技术人员泼了冷水，说他们关心的不是更好的技术，而是搜索的盈利。后来 Google 包装成了“更先进技术的新一代搜索引擎”的身份，逐渐取代了市场，并实现了盈利。

由于 PageRank 算法有非常高的知名度和普及度，我们接下来以 PageRank 算法为例讲述“并行计算 + 数据算法”的经典搭配，并且这种“海量数据并行处理、迭代多轮后收敛”的分析过程也跟其他的数据挖掘或者机器学习算法应用类似，能起到很好的参考作用。

下面是 PageRank 算法的公式：

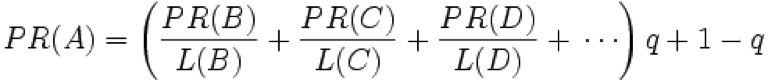
我们其实可以直接阐述该公式本身，并介绍如何使用并行计算套用上面公式得到各网页的 PageRank 值，这样虽然通过并行计算方式完成了 PageRank 计算，但是大家仍然不明白上面的 PageRank 公式是怎么来的。

我们把这个 PageRank 算法公式先放在一边，看看一个赌钱的游戏：
有甲、乙、丙三个人赌钱，他们的输赢关系如下：

甲的钱输给乙和丙
乙的钱输给丙
丙的钱输给甲

例如，甲、乙、丙各有本钱 100 元，按照以上输赢关系，玩一把下来：

甲输给乙 50 元、输给丙 50 元
乙输给丙 100 元
丙输给甲 100 元

如果仅是玩一把的话很容易算出谁输谁赢
但如果他们几个维持这样的输赢关系，赢的钱又投进去继续赌，这样一轮一轮赌下去的话，最后会是什么样子呢？

我们可以写个单机程序看看，为了方便计算，初始本钱都设为 1 块钱，用 x1，x2，x3 代表甲、乙、丙：
double x1=1.0,x2=1.0,x3=1.0;
用 x1_income，x2_income，x3_income 代表每赌一把后各人赢的钱，根据输赢关系：

double x2 income =x1/2.0;
double x3 income =x1/2.0+x2;
double x1_ income =x3;

最后再把各人赢的钱覆盖掉本钱，继续往下算。完整程序如下：

 
// Gamble 单机程序 <br></br>
public class Gamble<br></br>
{<br></br>
public static double x1=1.0,x2=1.0,x3=1.0;<br></br>
 
public static void playgame(){
<p>       double x2_income=x1/2.0;<br></br>        double x3_income=x1/2.0+x2;<br></br>        double x1_income=x3;<br></br>        x1=x1_income;<br></br>        x2=x2_income;<br></br>        x3=x3_income;<br></br>        System.out.println("x1:"+x1+", x2:"+x2+", x3:"+x3);<br></br> }                public static void main(String[] args){<br></br>        for(int i=0;i<500;i++){<br></br>        System.out.print(" 第 "+i+" 轮 ");<br></br>        playgame();<br></br>        }<br></br> }<br></br> }</p>

我们运行 500 轮后，看到结果如下：

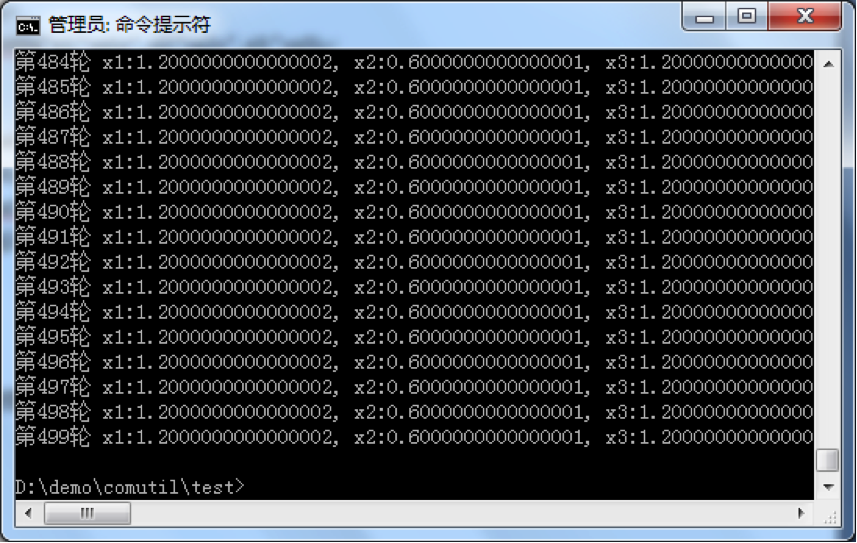
我们发现，从 107 轮后，各人的输赢结果就一直是
x1:1.2000000000000002, x2:0.6000000000000001, x3:1.2000000000000002
……

可能你都没想到会有这么个规律，这样一直赌下去，虽然各人每轮有输有赢，但是多轮后的输赢结果居然保持平衡，维持不变了。用技术术语来说就是多轮迭代后产生了收敛，用俗话来讲，就是玩下去甲和丙是不亏的，乙不服输再继续赌下去，也不会有扳本的机会的。

我们再把输赢关系稍微改一下：丙的钱输给甲和乙
double x2_income=x1/2.0+x3/2.0;
double x3_income=x1/2.0+x2;
double x1_income=x3/2.0;

运行 10000 轮后，发现又收敛了：
x1:0.6666666666666667, x2:1.0, x3:1.3333333333333333
…
不过这次就变成了“甲是输的，乙保本，丙是赢的”，我们发现收敛的结果可用于排名，如果给他们做一个赌王排名的话，很显然：“丙排第一，乙第二、甲第三”。

那么这样的收敛是在所有情况下都会发生吗，什么情况不会收敛呢？
我们回过头观察上面的输赢关系，甲、乙、丙三人互相各有输赢，导致钱没有流走，所以他们三人才一直可以赌下去，如果把输赢关系改一下，让甲只输钱，不赢钱，如下：
double x2_income=x1/2.0+x3/2.0;
double x3_income=x1/2.0+x2;
double x1_income=0;

那么运行下来会是什么结果呢？

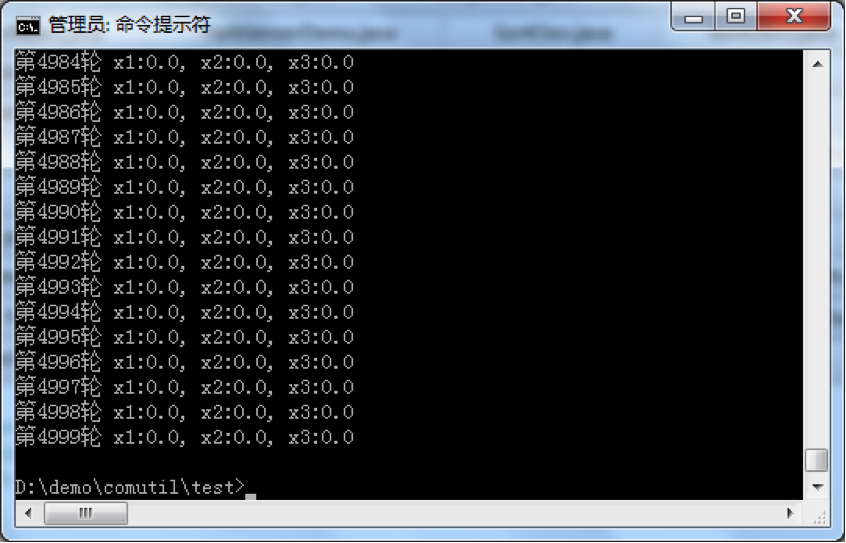
我们发现很多轮后，全部为 0 了。我们分析一下过程，第一轮后，甲的钱就输光了，没有赢得一分钱。但是乙和丙各有输赢，他们一直赌到 2000 多轮时，乙的钱全部输光了，甲乙都没钱投进来赌了，导致丙再也赢不到钱了，最后所有人结果都变为 0 了。

我们再分析一下输赢关系，甲的钱全部输给丙和乙后，丙跟乙赌，赢的多输的少，于是所有的钱慢慢都被丙赢走了，导致最后无法维持一个平衡的输赢结果。因此，如果我们要维持平衡和收敛，必须保证赢了钱的人不准走，必须又输给别人才行，让钱一直在三人圈里转不流失。换句话说，如果存在某人只输不赢，那么这个游戏就玩不下去。

赌钱游戏讲完了，我们再看看 PageRank 算法的公式：

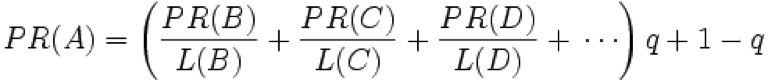
上面的 L(B) 代表页面 B 指向其他页面的连接数，我们举个例子：

假设有 A、B、C 三张网页，他们的链接关系如下：

A 包含 B 和 C 的链接
B 包含 C 的链接
C 包含 A 的链接

根据上面的公式，得到各网页 PR 值如下：

PR(B)=PR(A)/2;
PR(B)=PR(A)/2+PR©;
PR(A)=PR©;

可以回过头对照一下，把 A、B、C 改成甲、乙、丙就是上面举的赌钱游戏例子。

那么 q 是干吗的？公式里的 q 叫做逃脱因子，名字很抽象，目的就是用于解决上面赌钱游戏中“只输不赢”不收敛的问题，1-q 会保证其中一个 PR 值为 0 时计算下来不会全部为 0，那么加了这么一个 (…)*q+1-q 的关系后，整体的 PR 值会变化吗？

当每个页面的初始 PR 值为 1 时，0<=q<=1(计算时通常取值 0.8)，我们把所有页面的 PR 值相加看看，假设有 n 张网页：

PR(x1)+ PR(x2)+ …+PR(xn)
=( (PR(x2)/ L(x2)+ … )_q+1-q) + … + ( (PR(x1)/ L(x1)+ … )_q+1-q)
=(PR(x1) L(x1)/L(x1) + PR(x2) L(x2)/L(x2) + … + PR(xn) _L(xn)/L(xn))q + n(1-q)
=( PR(x1) + PR(x2) + … + PR(xn))_q + n - n_q
=n_q + n – n*q
= n

由于初始 PR 值为 1，所以最后所有页面的 PR 值相加结果还是为 n，保持不变，但是加上 (…)*q+1-q 的关系后，就避免了 PR 值为 0 可以寻求收敛进行排序。

当然实际应用中，这个公式还可以设计的更复杂，并可以通过高等代数矩阵旋转求解，我们这里只是为了理解原理，并不是为了做搜索算法，所以就不再深入下去了。

总结：世界的很多东西都是零和游戏，就像炒股，股民赚的钱也就是机构亏的钱，机构赚的钱也就是股民亏的钱，也许股民们应该研究一下 PageRank 算法，看看股市起起落落的背后是不是收敛了，收敛了说明炒下去永远别想解套，而且机构永远不会亏。

如何使用并行计算方式求 PR 值：
我们这里通过 fourinone 提供的各种并行计算模式去设计，思路方法可以有很多种。
第一次使用可以参考分布式计算上手demo 指南，开发包下载地址： http://www.skycn.com/soft/68321.html

思路一：可以采取工人互相合并的机制（工人互相合并及 receive 使用可参见 sayhello demo ），每个工人分析当前网页链接，对每个链接进行一次 PR 值投票，通过 receive 直接投票到该链接对于网页所在的工人机器上，这样经过一轮工人的互相投票，然后再统计一下本机器各网页所得的投票数得到新的 PR 值。但是这种方式，对于每个链接投票，都要调用一次 receive 到其他工人机器，比较耗用带宽，网页数量庞大链接众多时要调用很多次 receive，导致性能不高。

思路二：由于求 PR 值的特点是输入数据大，输出数据小，也就是网页成千上万占空间多，但是算出来的 PR 值占空间小，我们姑且用内存可以装下。因此我们优先考虑每个工人统计各自机器上的网页，计算各链接对应网页的所得投票，然后返回工头统一合并得到各网页的 PR 值。可以采用最基本的“总—分—总”并行计算模式实现（请参考分布式计算上手 demo 指南）。
并行计算的拆分和合并设计如下：

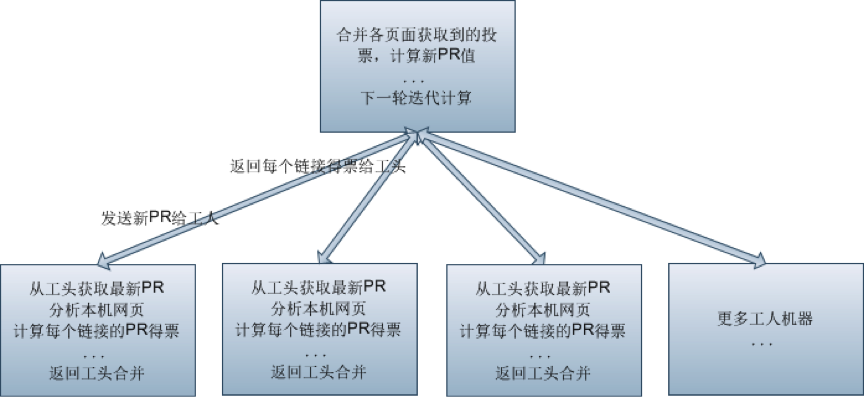
可以看到：

工人负责统计各自机器上网页的各个链接的 PR 得票。
工头负责合并累加得到各链接对应网页的新 PR 值，并迭代计算。

程序实现：

PageRankWorker：是一个 PageRank 工人实现，为了方便演示，它通过一个字符串数组代表包括的链接（实际上应该从本地网页文件里获取）
links = new String[]{“B”,“C”};
然后对链接集合中的每个链接进行 PR 投票
for(String p:links)
outhouse.setObj(p, pr/links.length);

PageRankCtor：是一个 PageRank 包工头实现，它将 A、B、C 三个网页的 PageRank 初始值设置为 1.00，然后通过 doTaskBatch 进行阶段计算，doTaskBatch 提供一个栅栏机制，等待每个工人计算完成才返回，工头将各工人返回的链接投票结果合并累加：
pagepr = pagepr+(Double)prwh.getObj(page);
得到各网页新的 PR 值（这里取 q 值为 1 进行计算），然后连续迭代 500 轮计算。

运行步骤：

1、 启动 ParkServerDemo（它的 IP 端口已经在配置文件指定）

java -cp fourinone.jar; ParkServerDemo

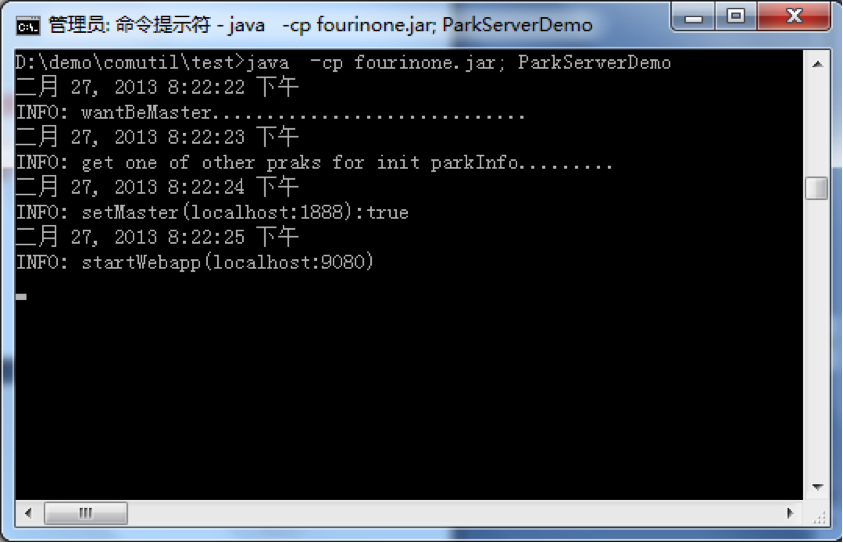
2、运行 A、B、C 三个 PageRankWorker，传入不同的 IP 和端口号
java -cp fourinone.jar; PageRankWorker localhost 2008 A

java -cp fourinone.jar; PageRankWorker localhost 2009 B

java -cp fourinone.jar; PageRankWorker localhost 2010 C

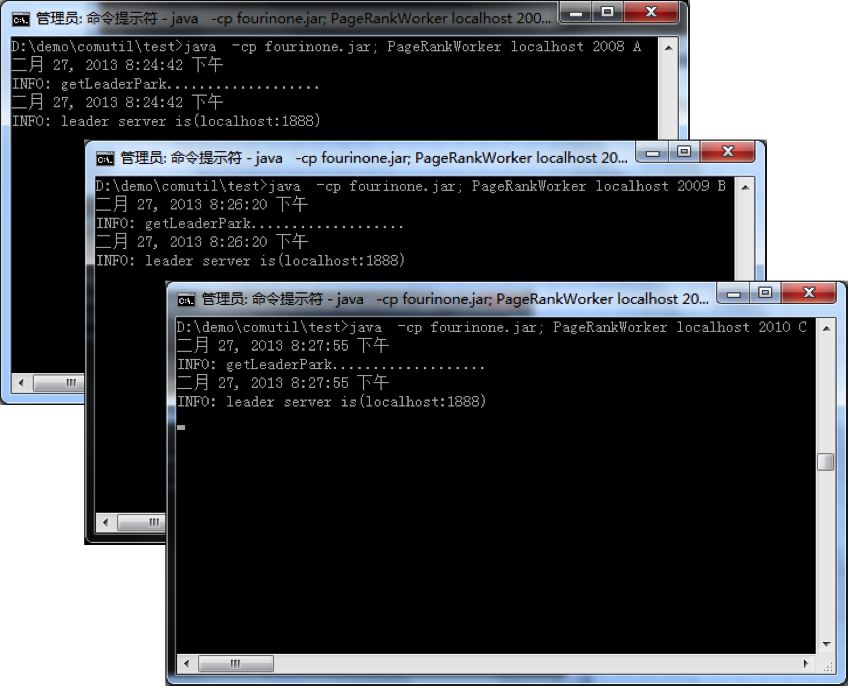
3、运行 PageRankCtor
java -cp fourinone.jar; PageRankCtor

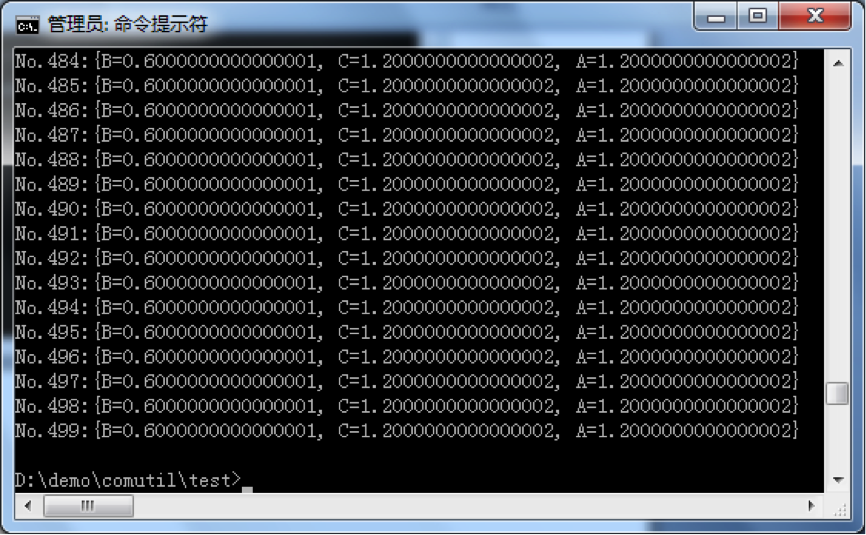
我们可以看到跟开始的单机程序的结果是一样的，同时各工人窗口依次输出了各自的 PR 值：

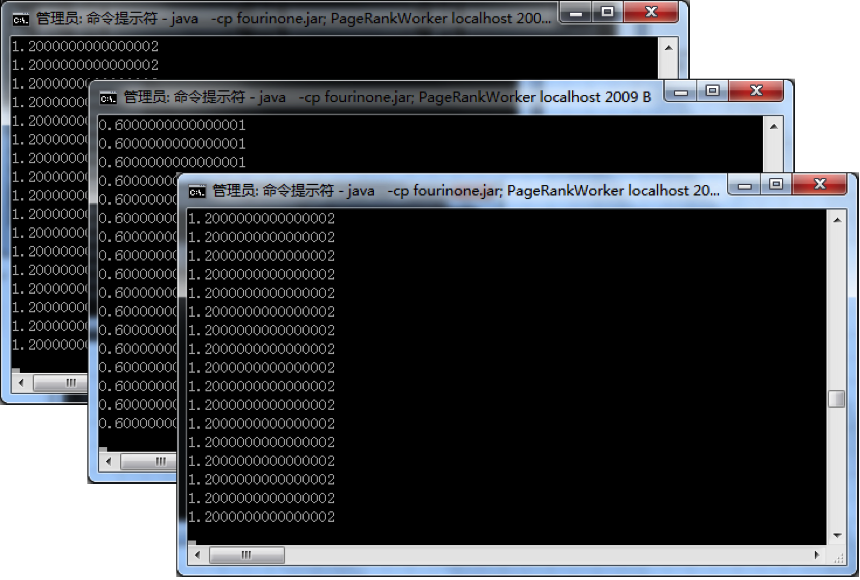
完整 demo 源码如下：

 
// ParkServerDemo
import com.fourinone.BeanContext;<br></br>
public class ParkServerDemo{<br></br>
       public static void main(String[] args){<br></br>
              BeanContext.startPark();<br></br>
        }<br></br>
}<p>// PageRankWorker import com.fourinone.MigrantWorker;<br></br> import com.fourinone.WareHouse;<br></br> import com.fourinone.Workman;</p><p>public class PageRankWorker extends MigrantWorker{<br></br>        public String page = null;<br></br>        public String[] links = null;<br></br>        public PageRankWorker(String page, String[] links){<br></br>               this.page = page;<br></br>               this.links = links;<br></br>        }</p><p><span>              </span>public WareHouse doTask(WareHouse inhouse) {<br></br>               Double pr = (Double)inhouse.getObj(page);<br></br>               System.out.println(pr);<br></br>               WareHouse outhouse = new WareHouse();<br></br>               for(String p:links)<br></br>                   outhouse.setObj(p, pr/links.length);// 对包括的链接 PR 投票 </p><p>                  return outhouse;<br></br>        }<br></br>        public static void main(String[] args){<br></br>               String[] links = null;<br></br>               if(args[2].equals("A"))<br></br>                   links = new String[]{"B","C"};//A 页面包括的链接 <br></br>               else if(args[2].equals("B"))<br></br>                   links = new String[]{"C"};<br></br>               else if(args[2].equals("C"))<br></br>                   links = new String[]{"A"};                                 <br></br>              PageRankWorker mw = new PageRankWorker(args[2],links);<br></br>               mw.waitWorking(args[0],Integer.parseInt(args[1]),"pagerankworker");<br></br>         }<br></br> }</p><p>// PageRankCtor<br></br> import com.fourinone.Contractor;<br></br> import com.fourinone.WareHouse;<br></br> import com.fourinone.WorkerLocal;<br></br> import java.util.Iterator;</p><p>public class PageRankCtor extends Contractor{<br></br>        public WareHouse giveTask(WareHouse inhouse){<br></br>               WorkerLocal[] wks = getWaitingWorkers("pagerankworker");<br></br>               System.out.println("wks.length:"+wks.length);                     <br></br>               for(int i=0;i<500;i++){//500 轮 <br></br>                   WareHouse[] hmarr = doTaskBatch(wks, inhouse);<br></br>                   WareHouse prwh = new WareHouse();<br></br>                       for(WareHouse result:hmarr){<br></br>                           for(Iterator iter=result.keySet().iterator();iter.hasNext();){<br></br>                               String page = (String)iter.next();<br></br>                               Double pagepr = (Double)result.getObj(page);<br></br>                               if(prwh.containsKey(page))<br></br>                                   pagepr = pagepr+(Double)prwh.getObj(page);<br></br>                                   prwh.setObj(page,pagepr);<br></br>                             }<br></br>                         }<br></br>                    inhouse = prwh;// 迭代 <br></br>                    System.out.println("No."+i+":"+inhouse);<br></br>                 }<br></br>                 return inhouse;<br></br>               }         <br></br>       public static void main(String[] args){<br></br>              PageRankCtor a = new PageRankCtor();<br></br>              WareHouse inhouse = new WareHouse();<br></br>              inhouse.setObj("A",1.00d);//A 的 pr 初始值 <br></br>              inhouse.setObj("B",1.00d);//B 的 pr 初始值 <br></br>              inhouse.setObj("C",1.00d);//C 的 pr 初始值 <br></br>              a.giveTask(inhouse);<br></br>              a.exit();        }<br></br> }</p>