在第一篇文章中,我们介绍了神经网络的基本概念以及 Tensorflow 的基本用法。 本文为系列的第二篇文章,将会介绍卷积神经网络。重点介绍经典的卷积神经网络,全卷积网络的基本概念和基本单元,以及卷积神经网络与神经网络的异同。最后通过实现一个在实际中有广泛应用的人脸关键点检测算法,介绍如何用 TensorFlow 构建卷积神经网络。
神经网络的发展历史
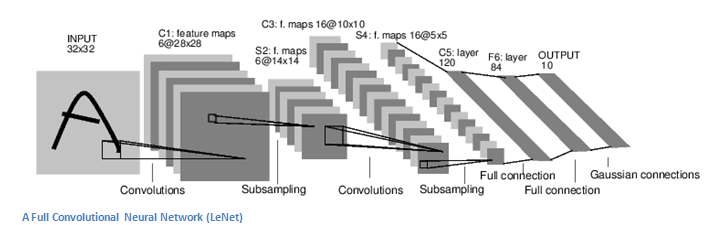
卷积神经网络(Convolutional Neural Network, CNN)的起源可以追溯到上世纪 60 年代。生物学研究表明,视觉信息从视网膜传递到大脑中是通过多个层次的感受野 (Receptive Field) 激发完成的,并提出了 Neocognitron 等早期模型。1998 年,深度学习三巨头之一的 Lecun 等,正式提出了 CNN,并设计了如下图所示的 LeNet-5 模型。该模型在手写字符识别等领域取得了不错的结果。
由于计算资源等原因,CNN 在很长时间内处于被遗忘的状态。二十多年后的 ImageNet 比赛中,基于 CNN 的 AlexNet 在比赛中大放异彩,并引领了 CNN 的复兴,此后 CNN 的研究进入了高速发展期。目前卷积神经网络的发展有两个主要方向:
- 如何提高模型的性能。这个方向的一大重点是如何训练更宽、更深的网络。沿着这一思路涌现出了包括 GoogleNet,VGG,ResNet,ResNext 在内的很多经典模型。
- 如何提高模型的速度。提高速度对 CNN 在移动端的部署至关重要。通过去掉 max pooling,改用 stride 卷积,使用 group 卷积,定点化等方法,人脸检测、前后背景分割等 CNN 应用已经在手机上大规模部署。
目前,CNN 是计算机视觉领域最重要的算法,在很多问题上都取得了良好的效果。因为篇幅关系,本文将主要介绍卷积神经网络的基础知识。
神经网络 vs 卷积神经网络
上篇文章中我们介绍了神经网络。神经网络在大数据处理,语言识别等领域都有着广泛的应用。但在处理图像问题时会许多问题:
- 参数爆炸
以 200x200x3 的图像为例,如果输入层之后的 hidden layer 有 100 个神经元,那么参数量会达到 200x200x3x100=1200 万。显然有如此多参数的模型是难以训练且容易过拟合的。 - 平移不变性
对很多图像问题,我们希望模型满足一定的平移不变性。 例如对图像分类问题,我们希望物体出现在图片的任何位置上,模型都能正确识别出物体。 - 局部相关性
在大数据等问题中,输入维度之间不存在显式的拓扑关系,因此适合使用神经网络(全连接层)进行建模。但对于计算机视觉的问题,输入图片的相邻像素之间存在天然的拓扑关系。例如,判断图片中某个位置是否有物体时,我们只需要考虑这个位置周边的像素就可以了,而不需要像传统神经网络那样将图片中所有像素的信息作为输入。
为了克服神经网络的上述问题,在视觉领域,我们需要一种更合理的网络结构。卷积神经网络,在设计时通过局部连接和参数共享的方式,克服了神经网络的上述问题,因而在图像领域取得了惊人的效果。接下来我们将详细介绍卷积神经网络的原理。
卷积神经网络
网络结构
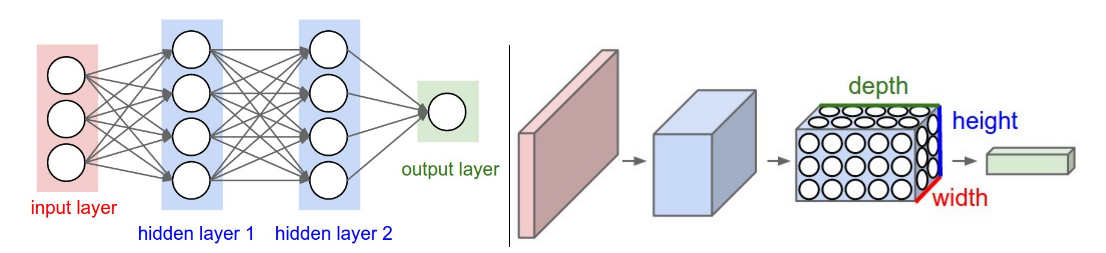
卷积神经网络和传统神经网络的整体结构大致相同。如下图所示,含有 2 层全连接层的传统神经网络和含有 2 层卷积层的卷积神经网络都是由基本单元堆叠而成,前一层的输出作为后一层的输入。最终层的输出,作为模型的预测值。二者的主要差别在于基本单元不同,卷积神经网络使用卷积层代替了神经网络中的全连接层。
和全连接层一样,卷积层中也含有可以学习的参数 weight 和 bias。模型的参数,可以按上一篇文章介绍的方法,在监督学习的框架下定义损失函数,通过反向传播进行优化。
卷积 (Convolution)
卷积层是整个卷积神经网络的基础。2D 卷积操作,可以看作是一个类似模板匹配的过程。如下图所示,将尺寸为\(h \times w \times d\) 的模板,通过滑动窗口的方式和输入进行匹配。滑动过程中,输入中对应位置的值和模板的权重的内积加一个偏移量\(b\),作为对应输出位置的值。\(w\),\(h\) 是模板的大小,统称为 kernel size,在 CNN 中,\(w\) 和\(h\) 一般会取相同的值。\(d\) 是模板的 channel 数量,和输入的 channel 数相同,例如对 RGB 图像,channel 数为 3。
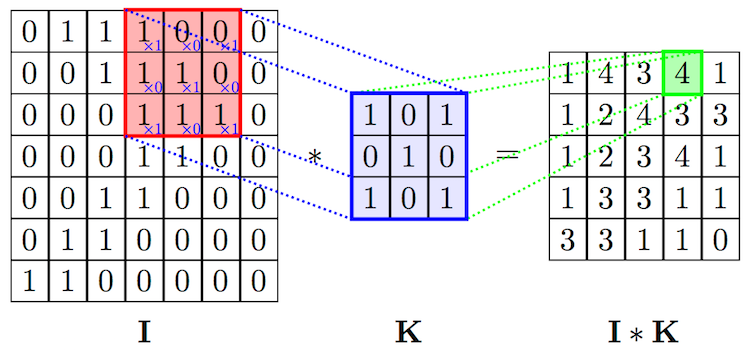
模板在卷积神经网络中常被称为卷积核(\(K\))或者过滤器(filter)。在标准卷积中,输出位置\((x,y)\) 对应的输出值可以表示成:
\({conv}(I, K)_{xy} = \sum_{i=1}^h \sum_{j=1}^w \sum_{k=1}^d {K_{ijk} \cdot I_{x + i - 1, y + j - 1, k}} + b\)
在 CNN 中,除了描述单个 filter 的\(h\),\(w\),\(d\) 3 个参数之外,还有 3 个重要的参数 depth, stride 和 padding:
- depth 指的是输出 channel 的数量, 对应于卷积层中 filter 的数量
- stride 指的是 filter 每次滑动的步长
- padding 指的是在输入四周补 0 的宽度。使用 padding 主要是为了控制输出的尺寸。如果不添加 padding,使用 kernel size 大于 1 的 filter 会使输尺寸出比输入小。在实际中经常会增加 padding,使得输入和输出的尺寸一致。
如下图所示,对 1D 的情况,假设输入尺寸为\(W\),filter 的尺寸为\(F\),stride 为\(S\),padding 为\(P\),那么输出的尺寸为\( (W - F + 2P)/S + 1\) 为。 通过设定\(P=(F-1)/2\),当\(S=1\) 时,输入和输出的尺寸会保持一致。2D 卷积的计算和 1D 卷积类似。

对比传统神经网络中的全连接层,卷积层实际上可以看成是全连接层的一种特例。首先是局部连接性,通过利用输入自带的空间拓扑结构,卷积神经网络只需考虑在空间上和输出节点距离在 filter 范围内的输入节点,其他边的权重都为 0。此外,对于不同的输出节点,我们强制 filter 的参数完全一致。但通过这种局部连接和参数共享,卷积层可以更好的利用图像中内在的拓扑关系及平移不变形,大大减少了参数,从而得到一个更好的局部最优解,使其在图像问题上有更好的性能。
在 tensorflow 中实现卷积层非常简单,可以直接调用 tf.nn.conv2d:
weight=tf.get_variable(shape=[kernel_size, kernel_size, input_size, depth])
bias = tf.get_variable(shape=[depth])
conv = tf.nn.conv2d(x, weight, strides=[1, 1, 1, 1], padding=‘SAME’)
conv_relu = tf.nn.relu(conv + bias)
池化 (Pooling)
在 CNN 网络中,除了大量的卷积层,我们也会根据需要,插入适量的池化层。池化层可以用来减少输入的尺寸,从而减少后续网络的参数与计算量。常见的池化操作(如 max pooling,average pooling),通常也可以提供一定的平移不变性。
我们以 max pooling 举例,max pooling 对 kernel size 范围内的所有值取 max,结果作为对应位置的输出。pooling 通常是对每个 channel 单独操作,因此输出的 channel 数和输入相同。池化层和卷积层类似,pooling 操作也可以理解为采用滑动窗口的方式,因此也有和卷积对应的步长 stride 和 padding 等概念。 下图所示就是一个 kernel size 和 stride 都为 2 的 max pooling 操作:
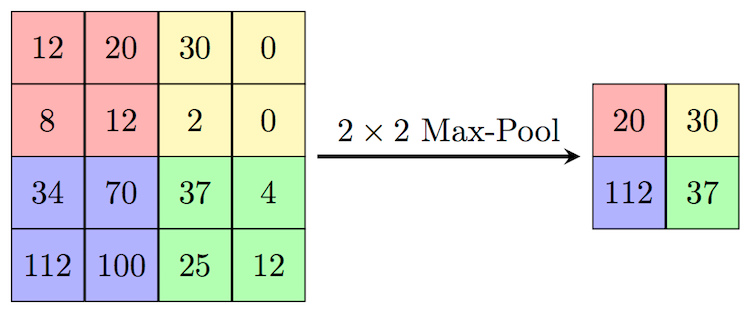
实际当中,池化层的参数有两种比较常见的配置,一种是 kernel size 和 stride 都为 2 的,这种设置池化过程中无重叠区域。另一种是 kernel size 为 3,stride 为 2 的有重叠 pooling。在 tensorflow 中实现池化层也非常简单:
tf.nn.max_pool(x, ksize=[1, size, size, 1], strides=[1, stride, stride, 1], padding=‘SAME’)
卷积神经网络的经典网络结构
介绍了卷积神经网络的基本组成模块之后,我们接下来介绍一下卷积神经网络的经典网络结构。从 1998 的 LeNet-5 开始,到 Imagenet 2012 的 AlexNet 模型,再到后来的 VGG 等一系列经典模型,基本都遵从了这个经典结构。
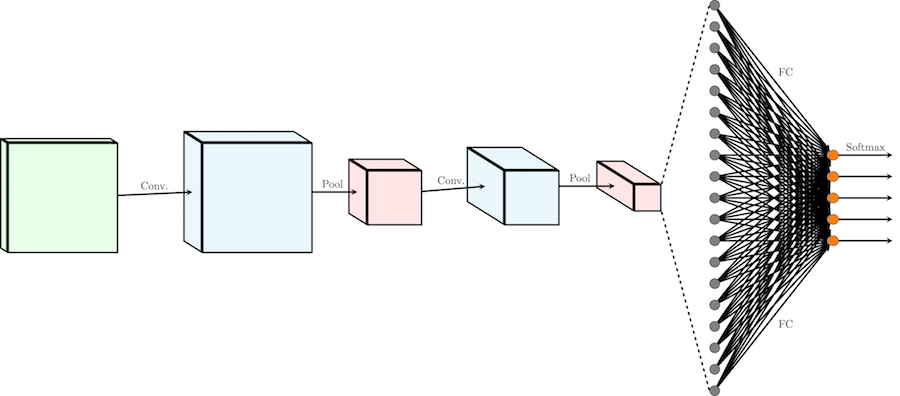
为了清晰,我们省略了卷积和全连接层之后的非线性激活函数。如上图所示,经典的卷积神经网络,可以分为三个部分:
- 一系列级联的 conv+pooling 层(有时会省略掉 pooling 层)。在级联的过程中,输入的尺寸逐渐变小,同时输出的 channel 逐渐变多,完成对信息从低级到高级的抽象。
- 一系列级联的全连接层。在卷积层到全连接层的交界处,卷积层的输出转化成一维的输入送入全连接层。之后根据任务的复杂程度,级联一系列全连接层。
- 最后的输出层,根据任务的需要,决定输出的形式。 如多分类问题,最后会接一个 softmax 层。
经典卷积神经网络,可以看作是一个输出尺寸固定的非线性函数。它可以将尺寸为 \(H \times W \times 3\) 的输入图片转化为最终的维度为\(d\) 的定长向量。经典卷积神经网络在图像分类、回归等问题上取得了巨大的成功。之后的实战部分,我们会给出一个回归问题的例子。
全卷积网络(Fully Convolution Network)
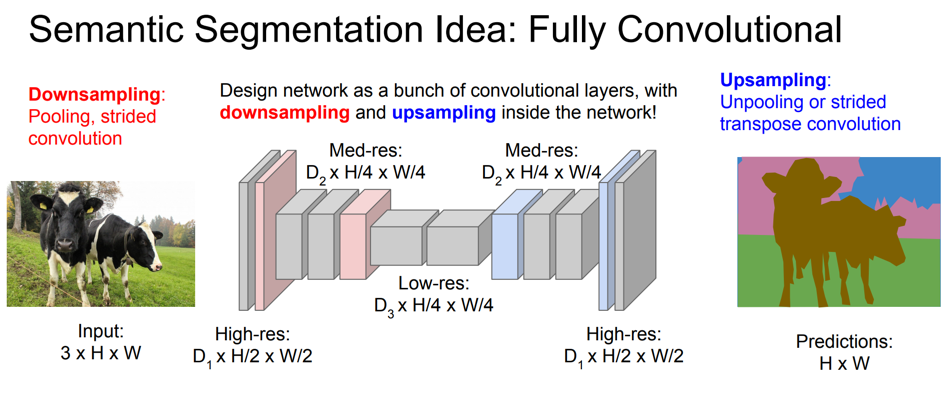
经典的卷积神经网络中由于有全连接层的存在,只能接受固定尺寸的图片作为输入,并产生固定尺寸的输出。虽然可以通过使用 adaptive pooling 的方式, 接受变长的输入,但这种处理仍然只能产生固定尺寸的输出。为了克服经典卷积神经网络的这种缺点,在物体分割等输出尺寸可变的应用场景下,我们不再使用全连接层。这种主要计算单元全部由卷积层组成的网络,被称为全卷积网络(FCN)。
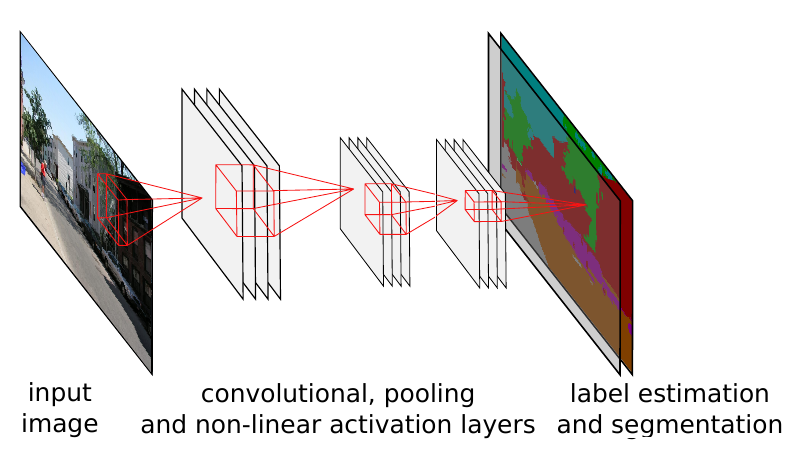
如上图所示,由于卷积操作对输入尺寸无限制,且输出尺寸由输入决定,因此全卷积网络可以很好的处理如分割等尺寸不固定的问题。全卷积网络,可以看成是一种输出尺寸随输入尺寸线性变化的非线性函数。它可以将尺寸为 \(H \times W \times 3\) 的输入图片转化为最终维度为\(H/S \times H/S \times d\) 的输出。 可以转化为这种形式的监督学习问题,基本都可以在全卷积网络的框架下求解。
反卷积(Deconvolution)
在全卷积网络中,标准的卷积 + 池化操作,会使输出的尺寸变小。对于很多问题,我们需要输出的尺寸和输入图片保持一致,因此我们需要一种可以扩大输入尺寸的操作。最常用的操作就是反卷积。
反卷积可以理解成卷积的逆向操作。这里我们主要介绍 stride>1 且为整数的反卷积。这种反卷积可以理解为一种广义的差值操作。以下图为例,输入是 3x3 的绿色方格,反卷积的 stride 为 2,kernel size 为 3,padding 为 1。在滑动过程中,对每个输入方格,其输出为对应的 3x3 阴影区域,输出值为输入值和 kernel 对应位置值的乘积。最终的输出为滑动过程中每个输出位置对应值的累加和。这可以看成是一种以 3x3 kernel 值为权重的差值操作。最外边的一圈白色区域无法进行完整的差值操作,因此可以通过设定 padding 为 1, 将周围的一圈白色区域去掉,最终的输出尺寸为 5x5。
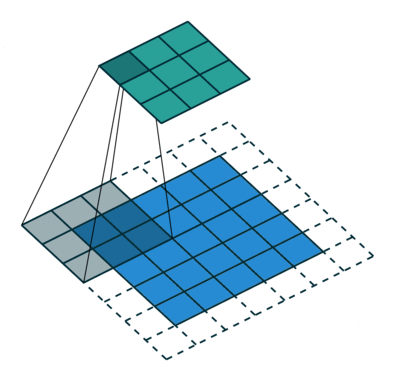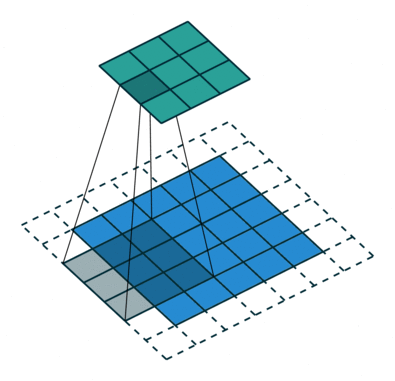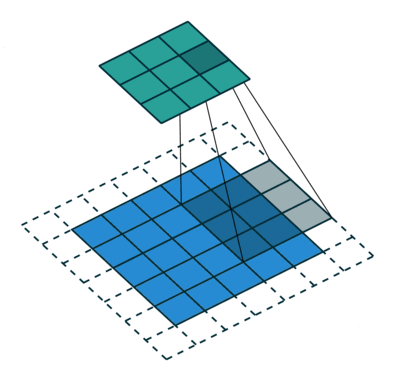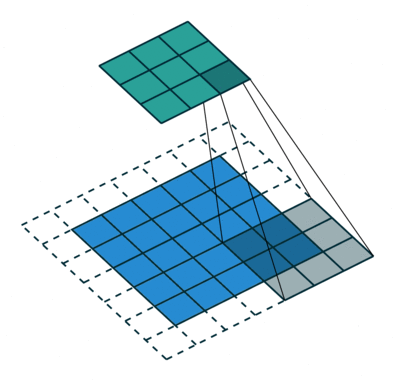
根据上面的描述,stride>1 且为整数的反卷积,如果固定反卷积 kernel 的取值为双线性差值 kernel,反卷积可以等价于双线性差值。而通过学习得到反卷积 kernel,相比固定参数的 kernel,可以更好的适应不同的问题,因此反卷积可以看成是传统差值的一种推广。和卷积类似,tensorflow 中已经实现了反卷积模块 tf.layers.conv2d_transpose 。
卷积神经网络在视觉识别中的应用
CNN 在视觉识别(Visual Recognition)中有着非常广泛的应用。我们接下来以视觉识别中的三大经典问题:分类 / 回归、检测和分割为例,介绍如何用 CNN 解决实际问题。
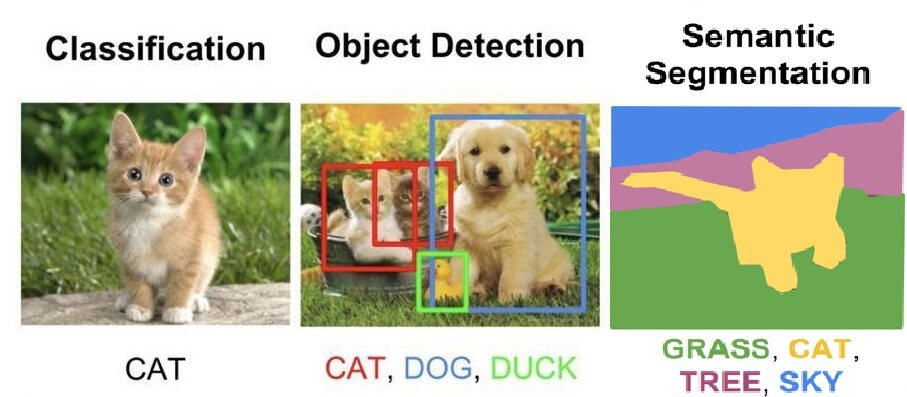
分类 / 回归 (classification/regression)
图像分类是指判别图像属于哪一 / 哪些预先指定的类别,图像回归是指根据图像内容判断图片属性的取值。分类和回归在实际中都有着广泛的应用。从物体分类,人脸识别,再到 12306 的验证码识别等,都可以抽象成标准的分类问题。类似的,人脸的关键点位置预测,人脸的属性预测(如年龄,颜值)等,也都可以抽象为标准的回归问题。目前视觉领域的应用,如果能抽象成输出为定长的分类或者回归问题,在有大量训练数据的情况下,通常都可以采用之前介绍的经典卷积神经网络框架解决。
检测 (detection)
检测问题通常是指判断出图片中是否有物体,以及该物体的位置。检测有 one-stage 和 two-stage 的方法。 因为篇幅关系,我们重点介绍在 FCN 框架下的 one-stage 方法。
按之前的介绍,FCN 可以看作是将\(H \times W \times 3\) 的输入图片,转化为\( H/S \times W/S \times d\) 输出的非线性函数。在 FCN 的框架下解决检测问题,我们可以预测每一个输出位置是否有物体,以及物体左上角、右下角相对于当前输入位置的偏移。 这样对每个输出位置,需要 5 维的向量来表示是否有物体,即 d=5。 定义了网络的输出之后,我们人工构造出对应的 ground truth,之后在监督学习的框架下,通过定义损失函数(l2 loss) 并进行反向传播,进行参数的学习。
分割 (segmentation)
分割问题是指给出图片中每个像素点的类别。 基于 FCN 的分割方法和上面介绍的 one-stage 的检测方法非常类似。 对一个多分类的分割问题,对输出的每一个位置,我们可以判断其所属的类别。 在 FCN 的框架下,对于 N 分类问题,输出为\(H/S \times W/S \times N\)。之后通过反向传播的方式进行训练。 分割和检测问题有一个区别是我们有时需要得到和输入图片同样大小的输出\((H \times W \times N)\),但卷积神经网络为了加速,通常会添加 pooling 层,减小中间卷积层的尺寸。 如下图所示,为了保证输出的尺寸满足要求,我们可以在网络的最后添加反卷积层进行补偿,从而获得更大尺寸的输出。
实战: 人脸关键点检测
人脸关键点检测是现在视觉领域比较成熟的一项应用,是活体检测,人类美化,人脸识别等高级应用的基础。本文最后通过一个人脸关键点检测的例子,展示如何用Tensorflow 实现图像回归类的应用。实验数据集采用Kaggle 比赛中的Faical Kerypoints Detection 数据集( https://www.kaggle.com/c/facial-keypoints-detection )。该数据集包含了 7094 张训练图片和 1783 张测试图片。数据集中的每一张人脸都有 15 个关键点的标注,图片的尺寸为 96x96。
L2 距离回归
Kaggle 比赛的目标是预测人脸上 15 个关键点的坐标,总共 30 个 float 值,属于标准的回归问题。我们选择采用最常见的 l2 距离,作为优化的目标。和第一篇文章中神经网络模型的代码结构一样,我们将代码分成了 3 个主要模块,分别是 Dataset 模块,Net 模块和 Solver 模块。
模型结构
inference
我们在 inference 函数中定义网络的主体结构。因为模型会重复用到全连接层和卷积层,因此我们将他们封装成函数linear_relu和conv_relu,从而方便复用代码。 网络结构上我们采用了比较简单的 3 层卷积,2 层全连接的结构。卷积层的输出通过tf.reshape转化成了全连接层可以接受的格式。因为是回归问题,我们直接将最后一层全连接层的结果作为输出。loss
为了简单,对于标准的回归问题,我们使用 mse 作为损失函数tf.reduce_mean(tf.square(predictions - labels), name='mse')metric
测试时,我们依旧使用 tensorflow 提供了 tf.metrics 模块,自动完成对每个 batch 的评价,并将所有的评价汇总。在这个例子里,我们是解决回归问题,因此可以使用tf.metrics.mean_squared_error计算均方误差。
def linear(x, output_size, wd=0):
input_size = x.get_shape()[1].value
weight = tf.get_variable(
name='weight',
shape=[input_size, output_size],
initializer=tf.contrib.layers.xavier_initializer())
bias = tf.get_variable(
'bias', shape=[output_size], initializer=tf.constant_initializer(0.0))
out = tf.matmul(x, weight) + bias
if wd != 0:
weight_decay = tf.multiply(tf.nn.l2_loss(weight), wd, name='weight_loss')
tf.add_to_collection('losses', weight_decay)
return out
def linear_relu(x, output_size, wd=0):
return tf.nn.relu(
linear(x, output_size, wd), name=tf.get_default_graph().get_name_scope())
def conv_relu(x, kernel_size, width, wd=0):
input_size = x.get_shape()[3]
weight = tf.get_variable(
name='weight',
shape=[kernel_size, kernel_size, input_size, width],
initializer=tf.contrib.layers.xavier_initializer())
bias = tf.get_variable(
'bias', shape=[width], initializer=tf.constant_initializer(0.0))
conv = tf.nn.conv2d(x, weight, strides=[1, 1, 1, 1], padding='SAME')
if wd != 0:
weight_decay = tf.multiply(tf.nn.l2_loss(weight), wd, name='weight_loss')
tf.add_to_collection('losses', weight_decay)
out = tf.nn.relu(conv + bias, name=tf.get_default_graph().get_name_scope())
return out
def pool(x, size):
return tf.nn.max_pool(
x, ksize=[1, size, size, 1], strides=[1, size, size, 1], padding='SAME')
class BasicCNN(Net):
def __init__(self, **kwargs):
self.output_size = kwargs.get('output_size', 1)
return
def inference(self, data):
with tf.variable_scope('conv1'):
conv1 = conv_relu(data, kernel_size=3, width=32)
pool1 = pool(conv1, size=2)
with tf.variable_scope('conv2'):
conv2 = conv_relu(pool1, kernel_size=2, width=64)
pool2 = pool(conv2, size=2)
with tf.variable_scope('conv3'):
conv3 = conv_relu(pool2, kernel_size=2, width=128)
pool3 = pool(conv3, size=2)
# Flatten convolutional layers output
shape = pool3.get_shape().as_list()
flattened = tf.reshape(pool3, [-1, shape[1] * shape[2] * shape[3]])
# Fully connected layers
with tf.variable_scope('fc4'):
fc4 = linear_relu(flattened, output_size=100)
with tf.variable_scope('fc5'):
fc5 = linear_relu(fc4, output_size=100)
with tf.variable_scope('out'):
prediction = linear(fc5, output_size=self.output_size)
return {"predictions": prediction, 'data': data}
def loss(self, layers, labels):
predictions = layers['predictions']
with tf.variable_scope('losses'):
loss = tf.reduce_mean(tf.square(predictions - labels), name='mse')
return loss
def metric(self, layers, labels):
predictions = layers['predictions']
with tf.variable_scope('metrics'):
metrics = {
"mse": tf.metrics.mean_squared_error(
labels=labels, predictions=predictions)}
return metrics
Dataset
images = np.vstack(df['Image'].values) / 255. # scale pixel values to [0, 1]
images = images.astype(np.float32)
label = df[df.columns[:-1]].values
label = (label - 48) / 48 # scale target coordinates to [-1, 1]
label = label.astype(np.float32)
def parse_example(example_proto):
features = {
"data": tf.FixedLenFeature((9216), tf.float32),
"label": tf.FixedLenFeature((30), tf.float32, default_value=[0.0] * 30),
}
parsed_features = tf.parse_single_example(example_proto, features)
image = tf.reshape(parsed_features["data"], (96, 96, -1))
return image, parsed_features["label"]
dataset = tf.contrib.data.TFRecordDataset(files)
dataset = dataset.map(self.parse_function)
Dataset 部分,我们使用了 tensorflow 推荐的 tfrecord 格式。通过TFRecordDataset函数读取 tfrecord 文件,并通过parse_example将 tfrecod 转换成模型的输入格式。tfrecord 作为一种定长格式,可以大大加快数据的读取速递。特别在使用 GPU 时,可以防止数据 io 成为性能的瓶颈。
Solver
通过模块化的设计,我们可以完全复用第一篇文章中的 Solver 代码,而不需要任何修改,进而提高代码的复用效率。
实验结果
file_dict = {
'train': os.path.join(args.data_dir, 'train.tfrecords'),
'eval': os.path.join(args.data_dir, 'test.tfrecords')
}
with tf.Graph().as_default():
dataset = Dataset(
file_dict=file_dict,
split='train',
parse_function=parse_example,
batch_size=50)
net = Net(output_size=30)
solver = Solver(dataset, net, max_steps=200, summary_iter=10)
solver.train()
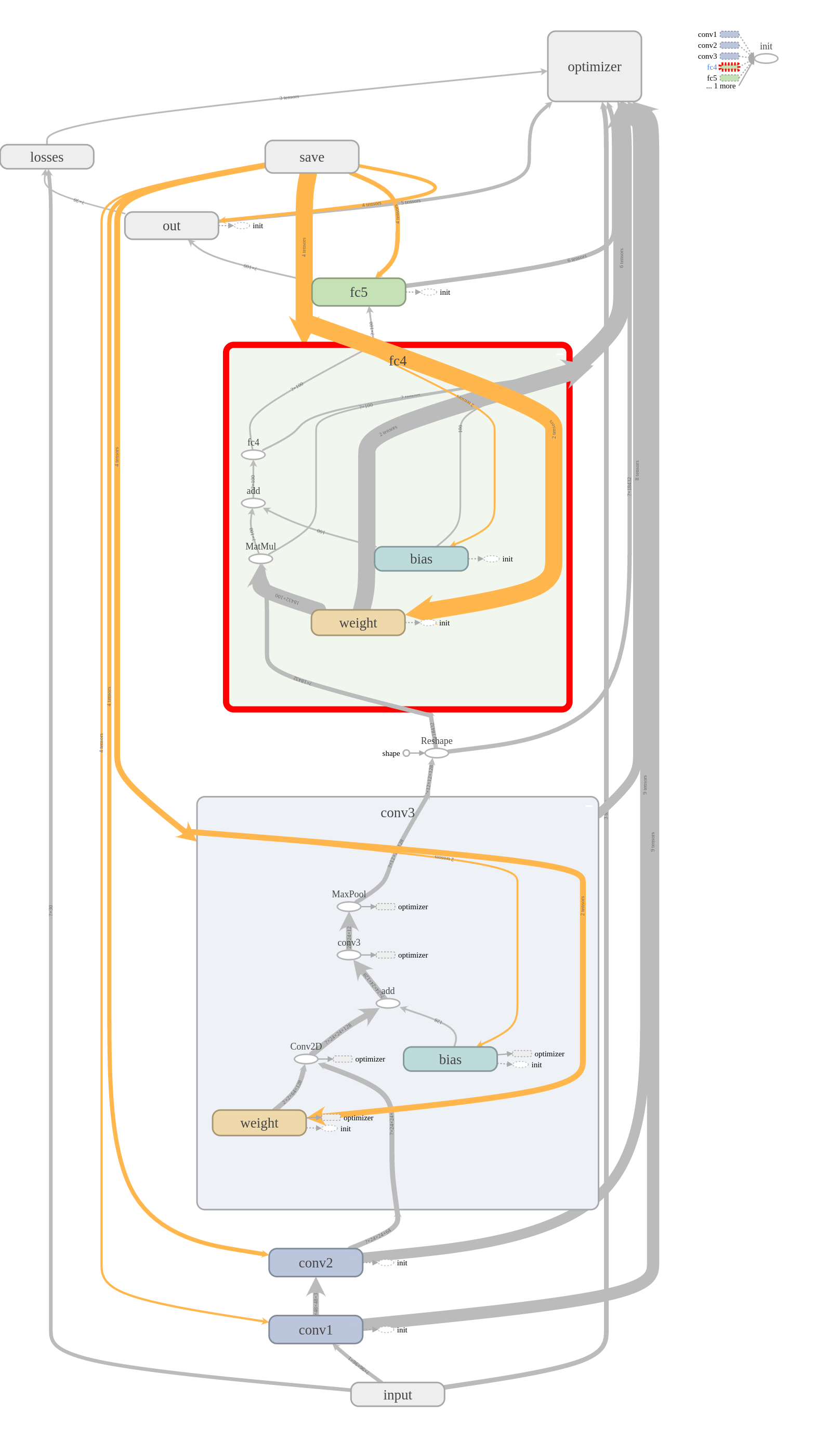
封装好借口之后,我们可以通过上面简单的代码,完成模型的训练。下图是 tensorboad 中可视化的网络结构、loss 的统计以及模型在测试图片上的效果:
step 10: loss = 0.0756 (136.2 examples/sec)
step 20: loss = 0.0230 (155.2 examples/sec)
step 30: loss = 0.0102 (149.1 examples/sec)
step 40: loss = 0.0071 (125.1 examples/sec)
step 50: loss = 0.0065 (160.9 examples/sec)
step 60: loss = 0.0081 (171.9 examples/sec)
step 70: loss = 0.0058 (148.4 examples/sec)
step 80: loss = 0.0060 (169.4 examples/sec)
step 90: loss = 0.0069 (185.4 examples/sec)
step 100: loss = 0.0057 (186.1 examples/sec)
step 110: loss = 0.0062 (183.8 examples/sec)
step 120: loss = 0.0080 (170.3 examples/sec)
step 130: loss = 0.0052 (185.8 examples/sec)
step 140: loss = 0.0071 (184.3 examples/sec)
step 150: loss = 0.0049 (170.7 examples/sec)
step 160: loss = 0.0056 (178.7 examples/sec)
step 170: loss = 0.0053 (173.2 examples/sec)
step 180: loss = 0.0058 (172.6 examples/sec)
step 190: loss = 0.0053 (172.5 examples/sec)
step 200: loss = 0.0056 (188.1 examples/sec)
mse: 0.140243709087
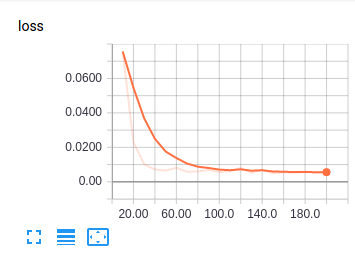
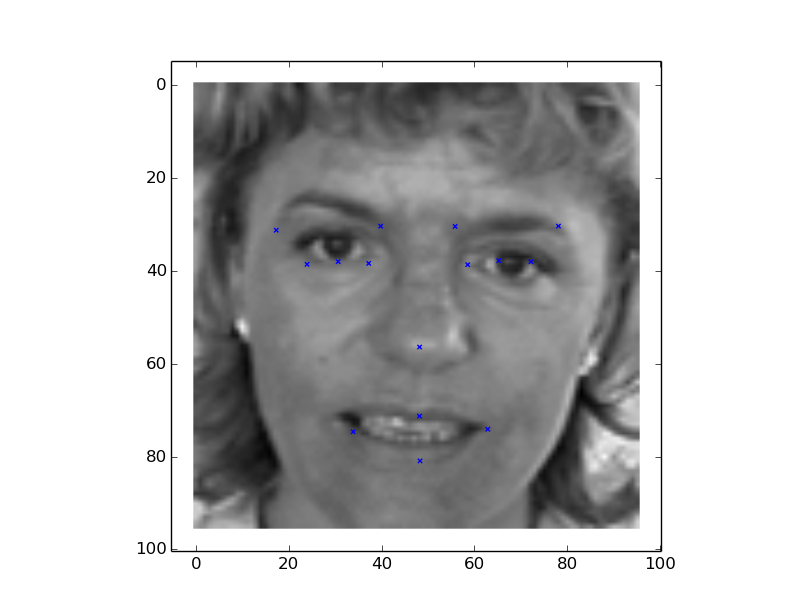
可以看到,一个 3 层卷积 +2 层全连接的经典卷积神经网络,就可以很好的解决人脸关键点检测的问题。在实际中,我们可以使用更复杂的网络和一些其他 trick 来进一步提高模型性能。