论文名称:τ-FPL: Tolerance-Constrained Learning in Linear Time(τ-FPL: 线性时间的约束容忍分类学习算法)
团队名称:iDST
作者:张翱,李楠,浦剑,王骏,严骏驰,查宏远
摘要
许多实际应用需要在满足假阳性率上限约束的前提下学习一个二分类器。对于该问题,现存方法往往通过调整标准分类器的参数,或者引入基于领域知识的不平衡分类损失来达到目的。由于没有显式地将假阳性率上限融合到模型训练中,这类方法的精度往往受到制约。本文提出了一个新的排序 - 阈值方法τ-FPL 解决这个问题。首先,我们设计了一个新的排序学习方法,其显式地将假阳性率上限值纳入考虑,并且展示了如何高效地在线性时间内求得该排序问题的全局最优解;而后将学到的排序函数转化为一个低假阳性率的分类器。通过理论误差分析以及实验,我们验证了τ-FPL 对比传统方法在性能及精度上的优越性。
研究背景
在疾病监测,风险决策控制,自动驾驶等高风险的分类任务中,误报正样本与负样本所造成的损失往往是不同的。例如,在高死亡率疾病检测的场景下,遗漏一名潜在病人的风险,要远高于误诊一名正常人。另一方面,两类错误的损失比也很难量化估计。在这种情况下,一个更加合理的学习目标是:我们希望可以在保证分类器假阳性率 (即错误地将负样本分类为正样本的概率) 低于某个阈值 τ 的前提下,最小化其误分正样本的概率。可以看到,由于问题的转换,传统的基于精度 (Accuracy),曲线下面积 (AUC) 等目标的学习算法将不再适用。
假阳性率约束下的分类学习,在文献中被称为 Neyman-Pearson 分类问题。现存的代表性方法主要有代价敏感学习 (Cost-sensitive learning),拉格朗日交替优化 (Lagragian Method), 排序 - 阈值法 (Ranking-Thresholding) 等。然而,这些方法通常面临一些问题,限制了其在实际中的使用:
- 需要额外的超参数选择过程,难以较好地匹配指定的假阳性率;
- 排序学习或者交替优化的训练复杂度较高,难以大规模扩展;
- 通过代理函数或者罚函数来近似约束条件,可能导致其无法被满足。
因此,如何针对现有方法存在的问题,给出新的解决方案,是本文的研究目标。
动机:从约束分类到排序学习
考虑经验版本的 Neyman-Pearson 分类问题,其寻找最优的打分函数 f 与阈值 b,使得在满足假阳性率约束的前提下,最小化正样本的误分概率:
我们尝试消除该问题中的约束。首先,我们阐述一个关键的结论:经验 Neyman-Pearson 分类与如下的排序学习问题是等价的,即它们有相同的最优解 f 以及最优目标函数值:
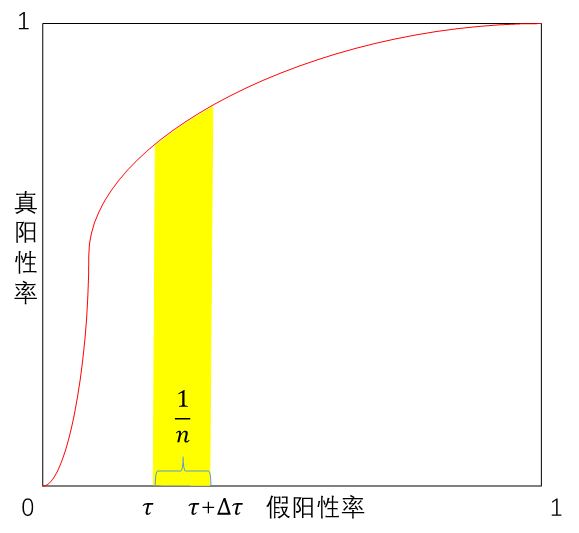
这里, f(x[j]^-) 表示取负样本中第 j 大的元素。直观上讲,该问题本身是一个 pairwise ranking 问题,其将所有的正样本与负样本中第τn 大的元素相比较。从优化 AUC 的角度,该问题也可看作一个部分 AUC 优化问题,如图 1 所示,其尝试最大化假阳性率τ附近的曲线下面积。
图 1: Neyman-Pearson 分类等价于一个部分 AUC 优化问题
然而,由于引入了取序操作符 [.],可以证明,即使将 0-1 损失用连续函数替换,该优化问题本身也是 NP-hard 的。因此,我们考虑优化该问题的一个凸上界:
这里 l 是任意 0-1 损失的凸代理函数 (convex surrogate function)。(2)仍然是一个排序问题,其尝试最大化负样本中得分最高的那部分的“质心”与正样本之间的距离。这个新问题有一些良好的性质:
- 通过设计高效的学习算法,我们可以在线性时间内求得该问题的全局最优解,这使其非常适合于大规模数据下的场景;
- 形式上显式地包含τ,无需引入额外的损失超参数 (cost-free);
- 最优解 f 有可理论保证的泛化误差界。
我们也可以从对抗学习 (Adversarial learning) 的角度,给出排序问题 (2) 的一个直观解释。读者可以验证,(2)与如下的对抗学习问题是等价的:
其中 k = τn,且
换句话说,排序学习问题 (2) 可以看作是在两个玩家——打分函数 A 与样本分布 B 间进行的一个 min-max 游戏。对于 A 给出的每个 f,B 尝试从负样本分布的集合△中给出一个最坏的分布 p,以最小化 A 的期望收益。该游戏达到纳什均衡 (Nash equilibrium) 时的稳点,也就是我们要求的最优解。
τ-FPL 算法总览
如上所述,τ-FPL 的训练分为两个部分,排序 (scoring) 与阈值 (thresholding)。在排序阶段,算法学习一个排序函数,其尝试将正样本排在负样本中得分最高的那部分的“质心”之前。阈值阶段则选取合适的阈值,将学到的排序函数转化为二分类器。
- 排序学习优化算法
考虑与 (2) 等价的对抗学习问题 (3),其对偶问题如下:
这个新问题不含任何不可导项,并且目标函数 g 是光滑的 (Smooth)。因此,我们可以使用投影梯度下降算法求解该问题,并利用加速梯度方法 (Nesterov) 获得最优的收敛率。
- 线性时间的变上界欧式投影
排序学习算法的一个关键步骤,是将梯度下降的解投影到可行集 Gamma_k 上。我们注意到,这个投影问题是⼀⼤类被⼴泛研究的欧式投影问题的推⼴。然而传统⽅法仅对一些特例可以⾼效求解,即便对于该问题的一个简化版本,也仅能达到 O(nlogn +τn^2) 的超线性复杂度。
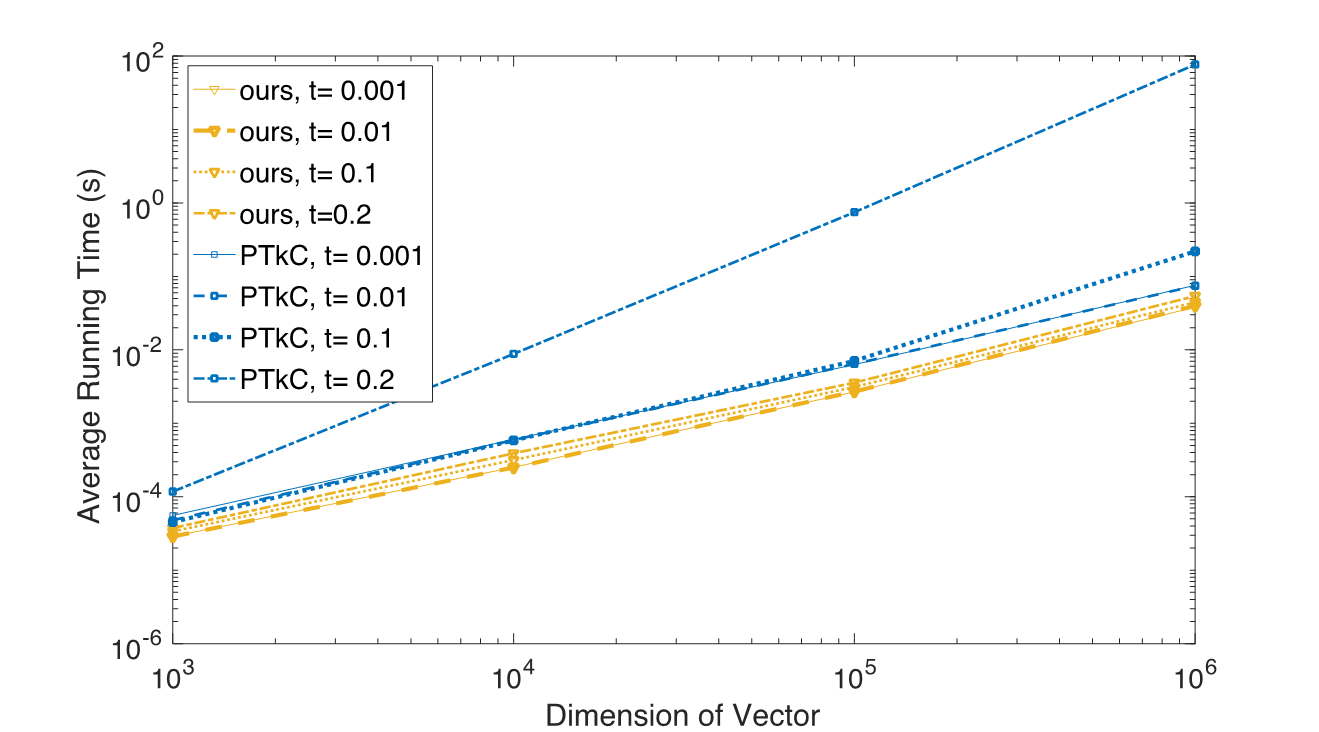
本文中,我们提出了一个算法,能够在 O(n) 的线性时间内高效地求解该投影问题,且其性能不受τ增长所带来的影响。该算法的核心是二分求根法与分治法的有效结合。根据 KKT 最优条件,我们将投影问题转换为一个求解分段线性方程组的问题,该方程组仅包含三个未知的对偶变量,且可以通过二分求根法获得指定精度的解。进一步地,利用方程组分段线性的特殊结构,以及对偶变量间“同变”的单调性质,我们可以在二分过程中逐步减少每次迭代的计算消耗,最终显著减少总的算法运行时间。实验中,我们观察到随着 n 与τ的增长,我们的算法较现有的求解该类问题的方法有一至三个数量级的性能提升,见图 2。
图 2:我们的方法与现存算法 (PTkC) 在求解简化版问题时的性能对比 (log-log 曲线)
- 阈值选择
阈值选择阶段,算法每次将训练集分为两份,⼀份训练排序函数, 另⼀份用来选取阈值。该过程可以进⾏多次,以充分利⽤所有样本,最终的阈值则是多轮阈值的平均。该方法结合了 out-of-bootstrap 与软阈值技术分别控制偏差及方差的优点,也适于并行。
理论结果
收敛率与时间复杂度 通过结合加速梯度方法与线性时间投影算法,τ-FPL 可以确保每次迭代的线性时间消耗以及最优的收敛率。图 3 将τ-FPL 与一些经典方法进行了对比,可以看到其同时具备最优的训练及验证复杂度。
泛化性能保证 我们也从理论上给出了τ-FPL 学得模型的泛化误差界,证明了泛化误差以很高的概率被经验误差所上界约束。这给予了我们设法求解排序问题(2)的理论支持。
图3: 不同算法的训练复杂度比较
实验结果
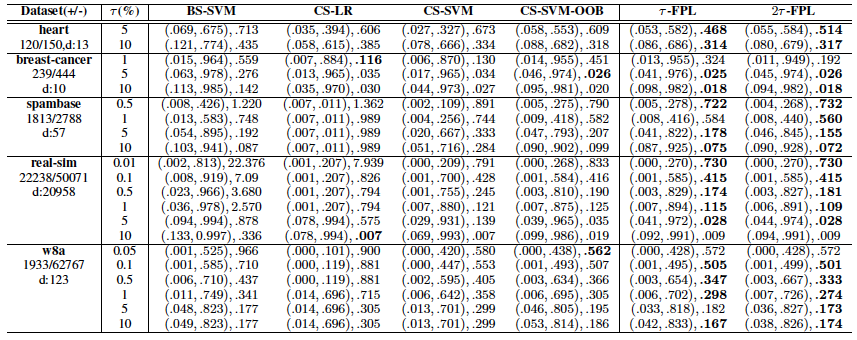
图4 报告了不同算法优化部分AUC 的效果,'N/A’代表该模型的训练无法在一周内完成。可以看到,τ-FPL 对于不同τ值,在大部分实验中都具有较好的表现。另外,其相比二分排序算法有明显的性能优势。
图5 比较了不同算法输出的分类器的分类性能。这里选取NP-score 作为评价标准,其综合考虑了分类器间的精度差异与违背假阳性率约束的惩罚。可以看到,采用OOB 阈值的算法在大部分情况下均可有效地抑制假阳性率在允许范围内。另外,即使采用同样的阈值选择方法,τ-FPL 也可以获得较代价敏感学习(CS-SVM-OOB) 更好的精度。
总结
在高风险分类任务中控制假阳性率是重要的。本文中,我们主要研究在指定的假阳性率容忍度τ下学习二分类器。为此,我们提出了一个新的排序学习问题,其显式地最大化将正样本排在前 τ% 负样本的质心之上的概率。通过结合加速梯度方法与线性时间投影,该排序问题可以在线性时间内被高效地解决。我们通过选取合适的阈值将学到的排序函数转换为低假阳性率的分类器,并从理论和实验两个角度验证了所提出方法的有效性。
如果您也有论文被 AAAI录用或者对论文编译整理工作感兴趣,欢迎关注AI前线(ai-front),在后台留下联系方式,我们将与您联系,并进行更多交流!


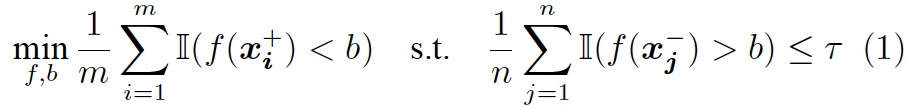
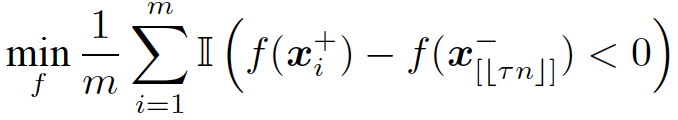
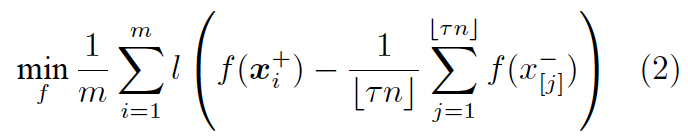
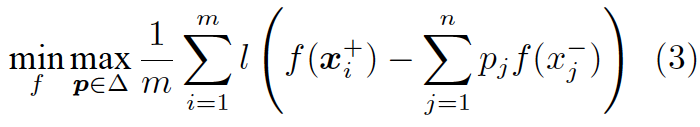
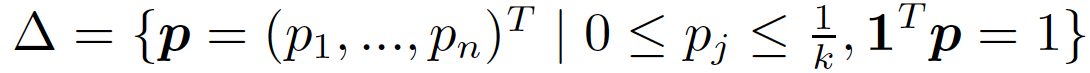
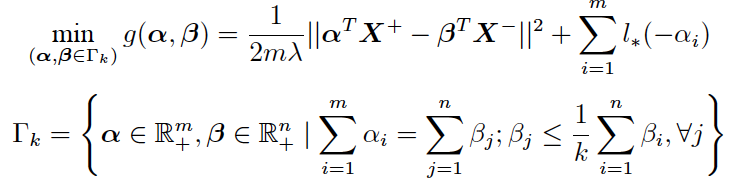














评论