一, 导语
拼图游戏很适合休闲放松的时候玩,所以在上大学的一段时间里,我比较喜欢玩,用来打发无聊的时光。
恰巧 2016 年李世石与阿尔法狗对弈,虽然我不懂围棋,但也跟着围观了每场比赛。当时我想既然下围棋能够用算法完成,那自动复原拼图应该是更简单的一件事,一定会有算法。人工智能课上老师也讲过复原拼图的\(A^*\) 算法, 上网查资料拼图的复原也大都用\(A^*\) 算法。不过对于复原拼图来讲, \(A^*\) 算法和瞎蒙的差别不大,如果 M 和 N 的值较小\(A^*\) 可以适用,当 M 和 N 过大时由于搜索空间变得太大就不可行了。那么有没有一种更明确的算法,可以计算出复原拼图的路径呢?
二, 基本概念
约定 1 :M*N 拼图是由 m 行 n 列个图块构成的拼图。
约定 2:用大写字母 P 表示拼图,\(P_i\) (i=1,2,3……n) 表示拼图所处的某一状态, \(P_e\) 表示拼图的原始状态或复原状态。
定义 1:复原拼图,可以表示为
\(P_i \overset{f}{\Rightarrow} P_e \),
即算法 f 作用到 \(P_i\) 上,使其回复到\(P_e\) 状态。
定义 2:拼图从\(P_i\) 到\(P_{i+1}\) 的状态变换为\(φ·P_i=P_{i+1}\) ,简写为\(φP_i=P_(i+1)\) ,即φ作用于状态\(P_i\) 使其变化为状态\(P_{i+1}\) 。
约定 3:M*N 拼图,我们用数字 1,2,3……,mn-1 作为图块的编号,用 mn 作为缺失图块的编号。用数字 1,2,3……,mn 表示位置的编号,位置的编号为从左至右,从上至下,依次递增,即左上角位置编号为 1,右下角位置编号为 mn。
约定 4:图块 \(a_j\) 直接称为 \(a_j\)。
以 3*3 拼图为例,它的位置编号如右图:在\(P_e\) 状态下每个图块所在的位置的编号等于图块的编号。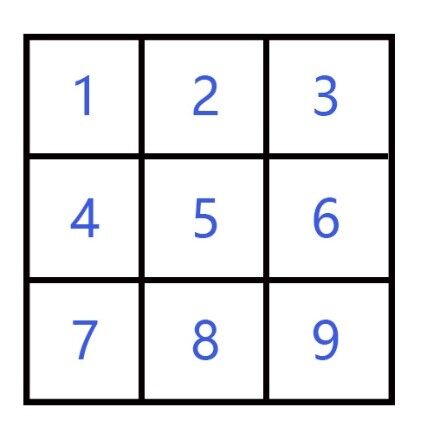
定义3:设mn=o,拼图在状态\(P_i\) 的具体表示为\(P_i=\begin{pmatrix} 1 & 2 & 3 & \cdots & j & \cdots & k & \cdots & o\\ a_1 & a_2 & a_3 & \cdots & a_j & \cdots & a_k & \cdots & a_o \end{pmatrix}\)
, 数列\(α_1,α_2,α_3,……,α_o\) 表示图块编号,数列\(1,2,3,……,o\) 表示位置,如果\(α_j=o\) ,代表\(a_j\) 为缺失的那个图块。
定义4:设\(a_i 所在的位置编号是C_{α_i},表示为\) \(a_j (C_{a_j })\)
或\(a_j (\frac{C_{a_j}-C_{a_j} (modn)}{n},C_{a_j} (modn)),\frac{C_{a_j}-C_{a_j} (modn)}{n}\) 为行号\(C_{a_j } (modn)\) 为列号。
拼图这样的表示方法和置换群的表示方法相同,事实上根据群的定义,拼图的所有状态构成群,可以吧拼图状态的变化看成置换群运算。
三, 等价性证明
本节将证明拼图状态变化与置换运算的等价,这是整个算法的理论基础。
证明:设\(P_i=\begin{pmatrix} 1 & 2 & 3 & \cdots & j & \cdots & k & \cdots & o\\ a_1 & a_2 & a_3 & \cdots & a_j & \cdots & a_k & \cdots & a_o \end{pmatrix}\) ,\(a_j=o\) ,且\(a_k\) 与缺失\(a_j\) 相邻,将\(a_k\) 移动到位置 j,由此\(P_{i+1}=\begin{pmatrix} 1 & 2 & 3 & \cdots & j & \cdots & k & \cdots & o\\ a_1 & a_2 & a_3 & \cdots & a_j & \cdots & a_k & \cdots & a_o \end{pmatrix}\)
在置换群中有 \((j,k)∙P_i=P_{i+1}\),在前文已经定义\(φ·P_i=P_{i+1}\) ,由\(\begin{cases} &(j,k)\cdot P_i=P_{i+1} \\ &\varphi \cdot P_i=P_{i+1} \end{cases}\Rightarrow (j,k)\Leftrightarrow \varphi \)
,即φ等价为对换。拼图一系列状态的变化,可以表示为一系列对换运算。
四, 算法描述
现在我们已经有了描述拼图的数学工具,本部分给出算法的描述。
1,自上而下,自左至右,按行复原,并设当前要复原的图块为\(a_j (C_{a_j} )\) 。
2,如果\(\frac{a_j-a_j (modn)}{n} <m-1\) ,\(a_j (modn) <n-1\) , 直接将\(a_j\) 移回位置\(a_j\) 。
3,如果\(\frac{a_j-a_j (modn)}{n} <m-1\) , \(a_j (modn) =n-1\), 将 \(a_j\) 移动到位置 \(a_j+1\),
再将\(a_j+1\) 移动到位置\(a_j+1+n\) , 最后同时复原这两个图块。
4,如果\(\frac{a_j-a_j (modn)}{n} =m-1\) ,\(a_j (modn) <n-1\) , 将\(a_j\) 移动到位置\(a_j+n\) ,
再将\(a_j+n\) 移动到位置 \(a_j+n+1\),最后同时复原这两个图块。
5,如果\(\frac{a_j-a_j (modn)}{n} =m-1\) , \(a_j (modn) =n-1\),顺时针或逆时针移动最后三块,直至回复到原来位置。至此拼图复原。
仅仅有这个算法还不够,我们还需要一个可以将\(a_j\) 移动到指定位置的算法。
五, 相对位置分析—— \(a_j\) 至目标
将某一图块移动到某一位置,是实现拼图复原基本思路的关键,也是最困难的步骤。这里分两步来实现:
- 将 mn 移动到\(a_j\) 附近,且 \(a_j\) 位置不变 。
- 将\(a_j\) 移动到目标位置。
如图:
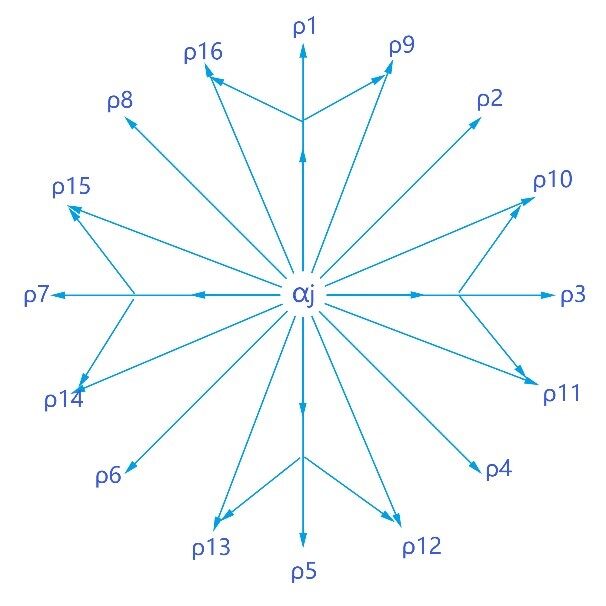
mn 可能处在相对\(a_j\) 的 8 个方位中的一个,将 mn 移动到 \(a_j\) 的正上、正下、正左、正右。 相对位置\(a_j\) 则有 16 种可能的方位。也就是说如果根据相对方位来规划路线需要分析 512 种情况。当然真实情况数要少于 512 种。
约定 5:命名\(\rho_1\) 为正上,\(\rho_2\) 为右上,\(\rho_3\) 为正右,\(\rho_4\) 为右下, \(\rho_5\) 为正下, \(\rho_6\) 为左下,\(\rho_7\) 为正左,\(\rho_8\) 为左上。
定义 5:\(\psi (x)\) 为目标位置, \(\psi\) 为目标。
\(\psi\) 是代表目标的占位符,并无其它意义。我们的目的是通过一系列对换将\(a_j\) 移动到目标位置\(\psi (x)\) 。
可以将\(\rho_9\) 至\(\rho_{16}\) 方位看成\(\rho_1\) 至 \(\rho_8\) 方位的复合,如同分解向量一样将其分解为两个方位,这样可以将 16 种情况减少到 8 种。
约定6:先正向再斜向。
定义6:\(\rho_a=\rho_b+\rho_c\) (8<a<=16;b=1,3,5,7;c=2,4,6,8), 符号+ 表示方位的复合运算。
表1 列出了\(\rho_9\) 至 \(\rho_{16}\) 的分解方式:
表1:方位分解表
分析基本的8 种方位,已知\(a_j (C_{a_j}) \) 可得\(\psi (x)\) ,推出:\(\begin{cases} & a_j(\frac{C_{a_j}-C_{a_j}modn}{n},C_{a_j}modn)\\ & \psi (\frac{x-xmodn}{n},xmodn) \end{cases} \)
定义7:\( \frac{x-xmodn}{n}- \frac{C_{a_j}-C_{a_j}modn}{n}=\Delta r\),\(\Delta r\) 为行差。
定义8:\(xmodn-C_{a_j}modn=\Delta c\) , \(\Delta c\) 为列差。
定义9:\(|\Delta r|-|\Delta c|=\Delta d\) , \(\Delta d\) 为行列差, 即行差的绝对值减去列差的绝对值。
表2 列出了方位与坐标差值的关系
表2:方位关系表
表3 列出了复合方位与坐标差值的关系
表3:复合方位关系表
六, 相对位置分析——mn 至\(a_j\)
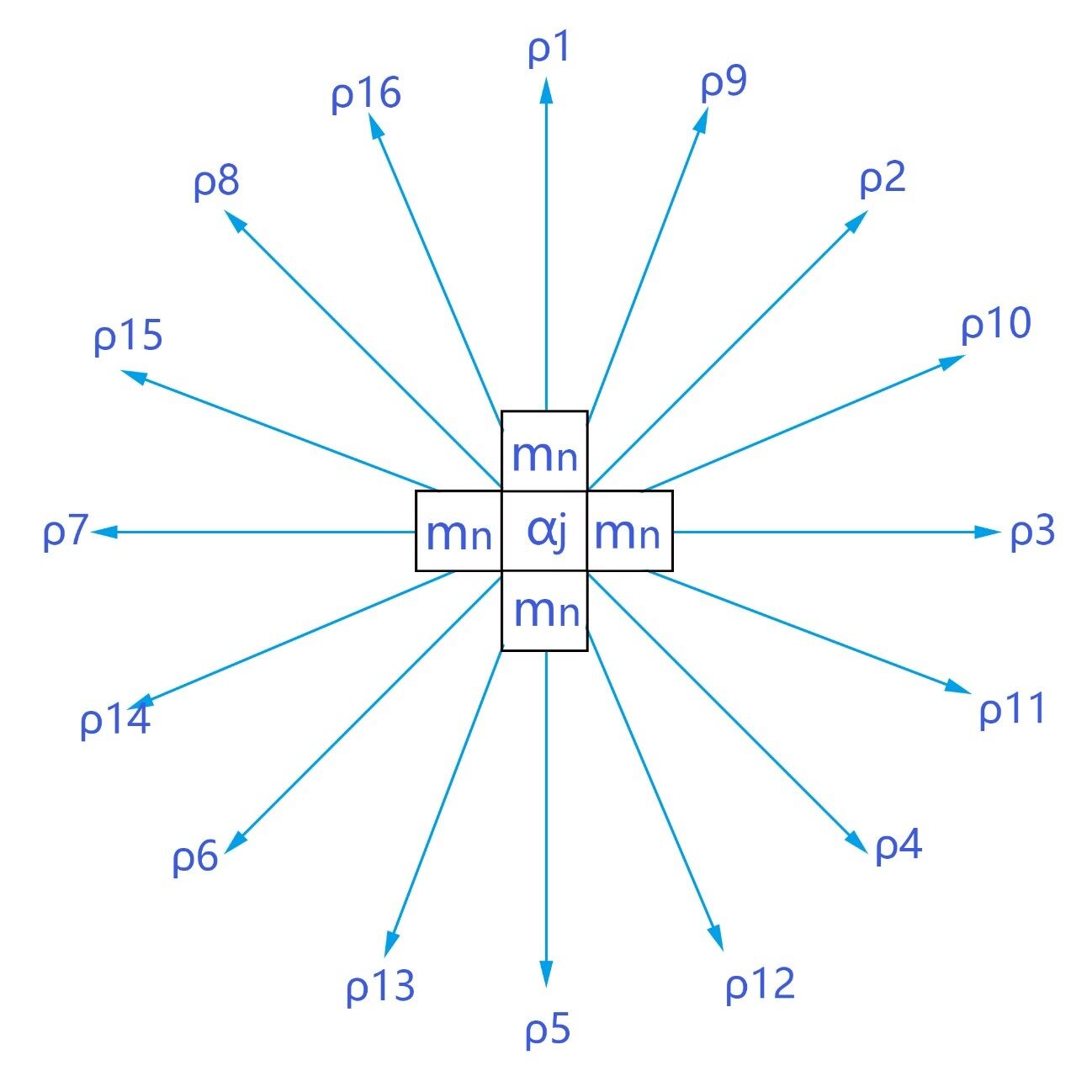
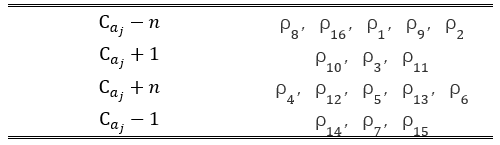
mn(它是缺失的那个,但我们仍认为它是一个存在的图块,mn 的特殊性是只有它才能和周围的图块相交换)至\(a_j\) 的相对位置仍然是任意的,但是将 mn 移动到想要的位置则简单一些。分析两者相对位置的原因是,\(a_j\) 的移动需要借助 mn,所以我们要根据\(a_j\) ,将 mn 移动到合适的位置。有四个带选取的位置分别是:\(C_{a_j }-1,C_{a_j }+1,C_{a_j}-n,C_{a_j}+n\)
如图划分了合适的位置与方位\(\rho\) 的关系,
表 4 与上图对应
表 4
不管两者如何对应,我们的目的本质是将 mn 移动到四个位置中的一个。
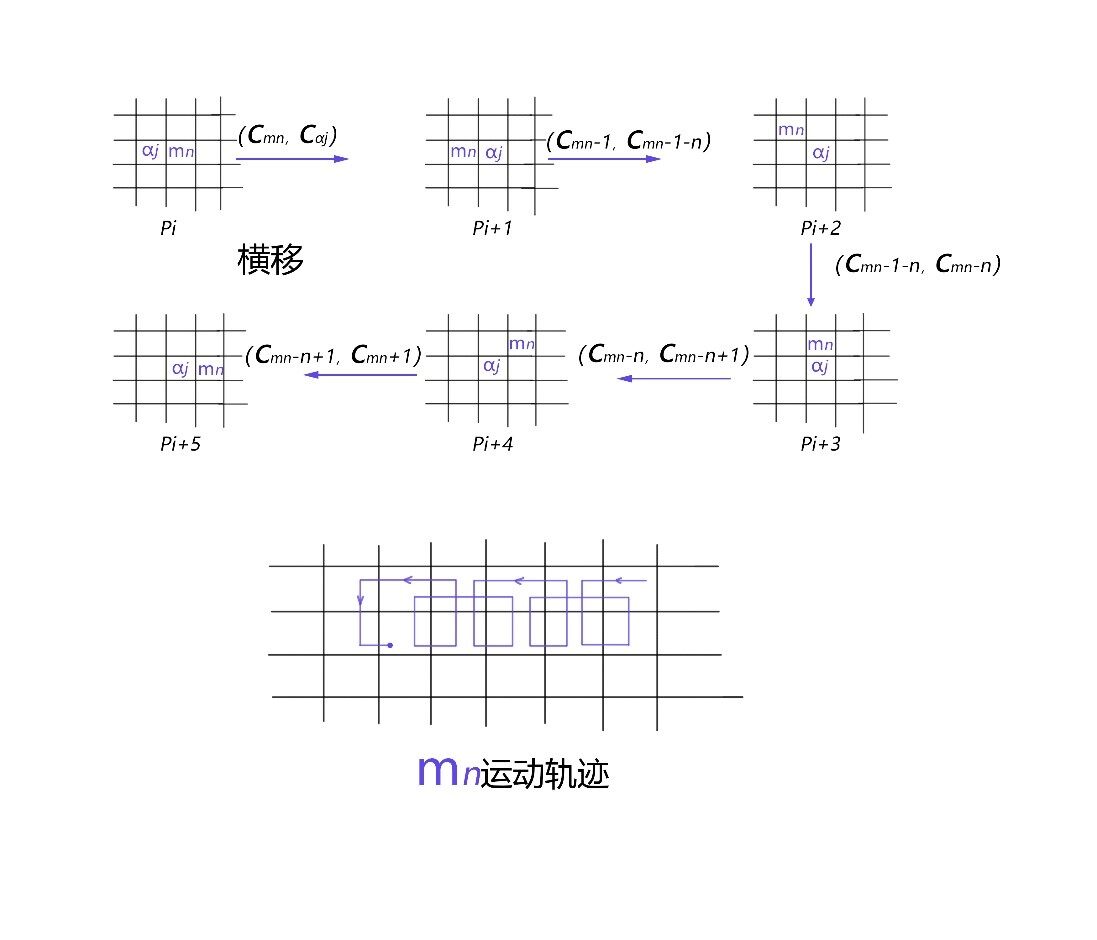
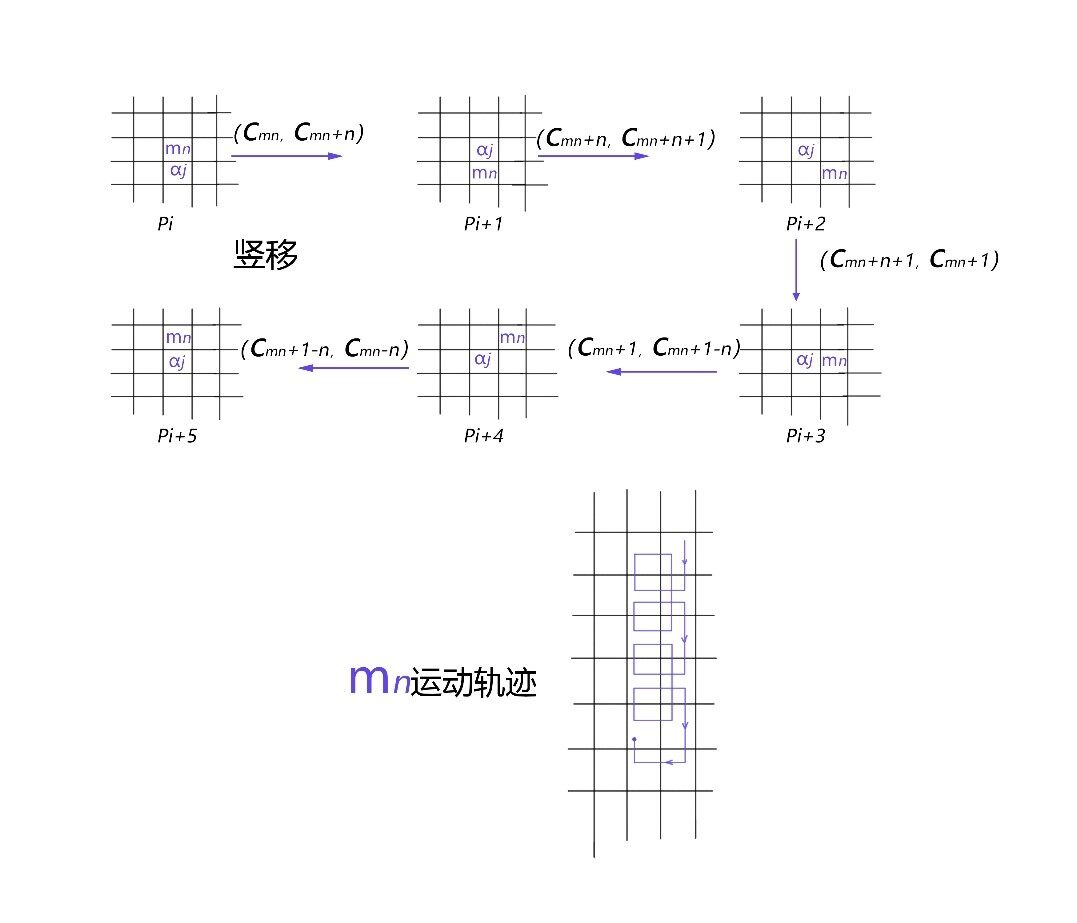
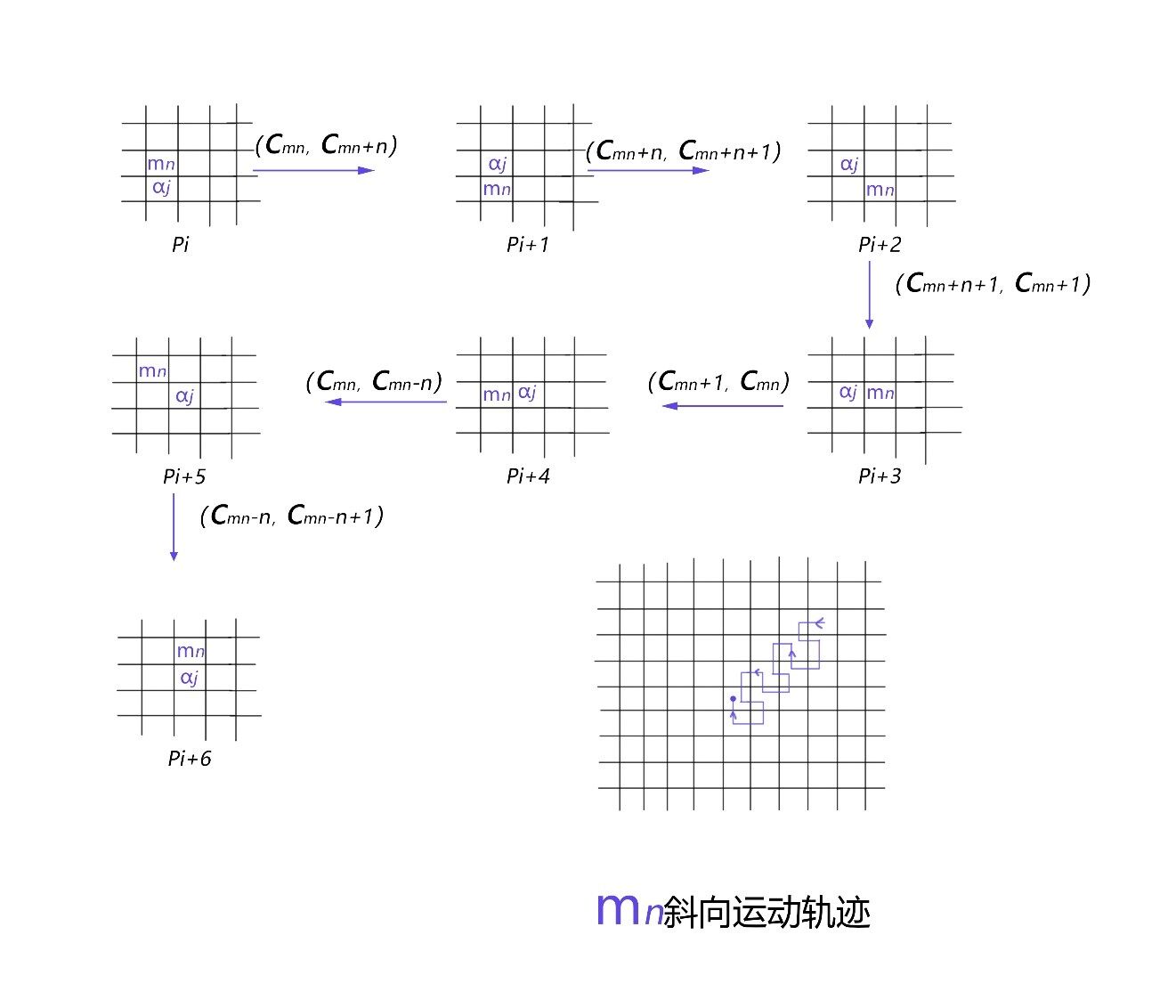
约定 7:将 mn 移动到\(a_j\) 附近,优先竖向移动,再横向移动。
七, 拼图移动策略
我们首先要考虑如何把 mn 移动到合理的位置,上图只描述了可能的移动路径。在真正的情况中可以遵守以下策略:优先竖向移动,mn 在到达合理位置是不应改变\(a_j\) 的位置。
移动\(a_j\) 到目标位置,要完成这个任务,其实更应关注 mn 如何移动,mn 作为缺失块,周围图块只能移动到 mn 所在的位置。这时 mn 的移动轨迹,具有周期性,mn 的轨迹也能用公式表示出来。
八, 拼图移动定理
我们已将定义了很多概念,也做了很多约定。但是到目前为止我们还没有充分的利用起它们。尤其是拼图的状态变化可等价于对换运算,我们还未用到。后面的公式显示了数学的威力。
已知 \(a_j (C_{a_j} )\),\(mn(C_{mn} )\) , \(\psi (x_1),\psi (x_2)\) 为 \(a_j\) 要到达的目标, \(\Delta r_1, \Delta c_1, \Delta d_1\) 为\(a_j\) 与目标\(\psi (x_1)\) 的行差、列差、行列差, \(\Delta r_2, \Delta c_2, \Delta d_2\) 为 mn 与目标\(\psi (x_2)\) 的行差、列差、行列差。
定理 1:将 mn 竖向移动\(\Delta r_2\) (-m<\(\Delta r_2\) <m) 行, 拼图起始状态为\(P_i\) , 等价于
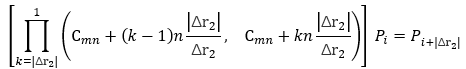
定理 2:将 mn 横向移动\(\Delta c_2\) (-n<\(\Delta c_2\) <n ) 列,拼图起始状态为 \(P_i\), 等价于
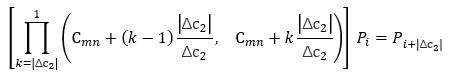
定理 3:将\(a_j\) 竖向移动\(\Delta r_1\) (-m<\(\Delta r_1\) <m) 行,拼图起始状态为\(P_i\) , 等价于
或
定理 4:将\(a_j\) 横向移动\(\Delta c_1\) (-n<\(\Delta c_1\) <n ) 列,拼图起始状态为\(P_i\) , 等价于
或
定理 5:将\(a_j\) 斜向移动 \(\Delta r_1\) (-m<\(\Delta r_1\) <m) 行\(\Delta c_1\) (-n<\(\Delta c_1\) <n ) 列,且 \(|\Delta r_1|=|\Delta c_1|\),
拼图起始状态为\(P_i\) , 等价于
定理中的公式很复杂,但是有了它们我们设想的算法便能实现。
九, 真实情况分析
复原拼图遇到的路径状况数目要少一些,而且有以下规律:
设当前刚复原\(a_j\) 且\(0<jmodn<n-1\) 。
- mn 所在的位置必然在 j+1 或 j+n。
- \(a_{j+1}\) 必然在 mn 的左下、正下、右下、正右、右上、正左方位中的一个。
- \(a_{j+1}\) 可能在位置 j+1 或任何一个大于 j+1 的位置。
- 如果\(a_{j+1}\) 不在位置 j+1 ,则\(j+1-(j+1)modn<C_{a_j}-C_{a_j} modn\) 。
这四条规律可以稍微降低算法实现的难度。同时复原拼图时有一条限制:不能破坏已复原的图块。
十, 与\(A^*\) 算法的比较
这个算法暂且命名为:拟人策略算法。
在文章开头我说过 \(A^*\) 算法和瞎蒙没啥区别,如果不在这里说出理由,恐怕要受人指摘了,毕竟人工智能课上老师可是重点讲过\(A^*\) 算法。由于我没有相关\(A^*\) 算法的实现,在这里只在理论上比较两种算法的优劣,并分别论述。
可还原拼图的状态数呈阶乘式的增长,4*4 拼图的状态数为\(\frac{16!}{2}\) ,5*5 拼图的状态数为\(\frac{25!}{2}\) ,m*n 拼图的状态数为 \(\frac{(mn)!}{2}\)。\(A^*\) 算法采用预估函数剪去不必要的分支,假设这个预估函数由图块与本来位置的距离之和决定。 \(P_i\) 的预估值不会超过\((mn)^3\) ,随着 m*n 的增大会有\((mn)^3\ll \frac{(mn)!}{2}\) 。当 m*n 较小时,剪枝还能实现,当 m*n 较大时 \(A^*\) 算法必然要搜索巨大的状态空间,这会是灾难。另外,预估函数和拼图复原并不会有必然的关系,某一状态预估函数的值小不一定意味着它好复原。
拟人策略算法与之最大的区别是它不进行状态空间搜索,它按照人类复原拼图的模式进行复原。实际上我们可以估算出一个人复原拼图需要多少次交换,按照上文给出的算法,\(a_j\) 回到自己的位置大概会经过\(\frac{m+n}{2}\) 格如果\(a_j\) 每移动一格需进行 6 次交换,对于 m*n 个图块回到自己的位置会需要\(\frac{m+n}{2}*6*mn=3mn(m+n)\) ,将 mn 移动到 \(a_j\) 附近估计需\(\frac{m+n}{2}\) 次交换,m*n 个图块就需要\(0.5mn(m+n)\) 次交换,两者总计 \(3.5mn(m+n)\) 次交换。如果实现这个算法,它的时间复杂度可能会正比于\((mn)^2\) 。这是个很粗略的估计,仅供参考。




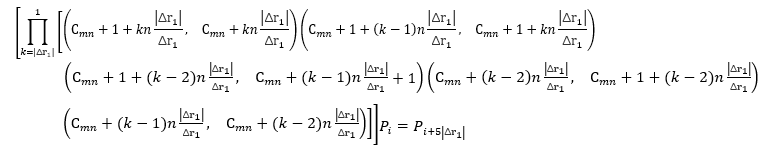
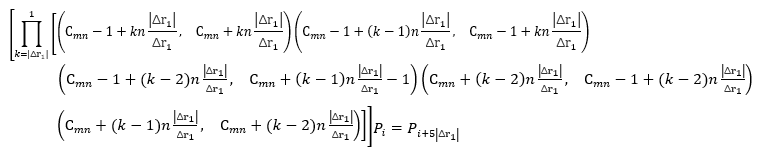
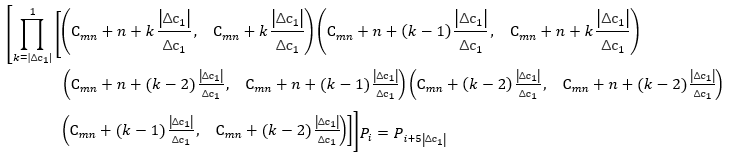
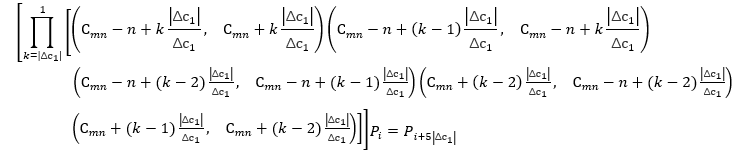
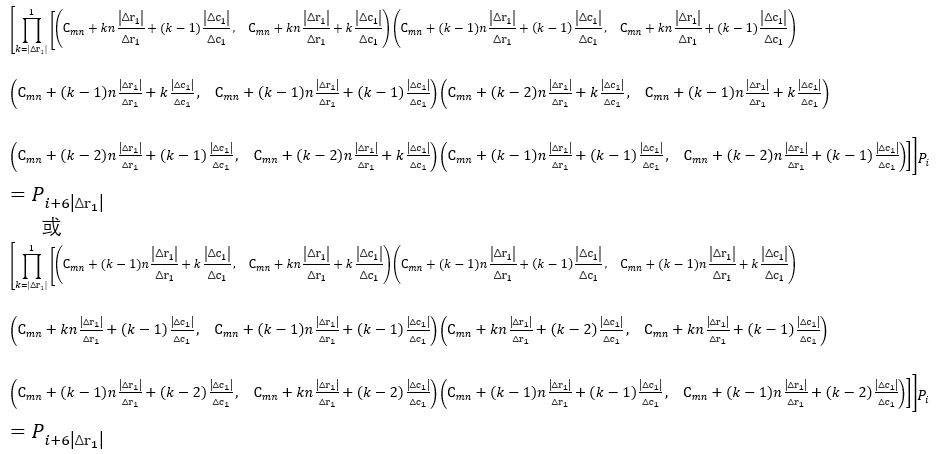







评论