谷歌训练出能安全通信的“人工智能”

随着人工智能技术的发展，人们可以训练神经网络解决越来越复杂的问题。不久之前，基于神经网络和决策树的 AlphaGo 击败了世界围棋冠军李世石。虽然这一成果极大刷新了世人对人工智能技术的认识，纷纷感慨人工智能摘走了人类智慧王冠上的明珠，但实际上目前还有很多问题领域等着神经网络的研究者们去探索。

在漫长的人类文明发展史中，人们对信息保护的重视程度一直不亚于对信息获取的重视程度。据古罗马随笔作家修托尼厄斯的记载，凯撒经常使用“密文”给他的朋友写信。在传递军事信息时，必须考虑信息被第三方截获的可能性。因此凯撒与他的将军们事先约定好一套变换规则，发信方将正常排列的文字序列变换为另一串文字序列，以此作为通信的文本发送给收信方。收信方收到这样的文本后要根据事先约定的变换规则把它恢复成原来的文字序列。这样，即便这个文本在通信途中被敌人截获，他们得到的也只是一串莫名其妙的文字，无法获悉其中隐藏的信息。

我们在互联网中进行通信时也是依靠类似的机制来保证信息的机密性和完整性。只是随着计算能力的发展，现在所采用的算法和协议要比古代复杂得多。但加解密的机制依然是通过一系列的程序步骤来实现的。

那么神经网络能否学会如何安全的通信呢？毕竟最简单的神经网络连加解密中最基本的亦或运算都不会。带着这个问题，谷歌大脑团队中的 Mart́ın Abadi 和 David G. Andersen 建立了一个小型的生成式对抗网络（GAN）来模拟传统的通信过程。这个网络由密码界的三个老朋友组成，发信方Alice、收信方Bob、窃听者Eve。

由于目的是探索普通的神经网络能否学会安全的通信，所以这些神经网络的结构能学会异或运算这样的混合函数就足够了。因此，Mart́ın 和David 采用了“混合与变换”的结构。第一层是一个全连接层，即输出的位数与输入的位数相等；然后是一系列的卷积层，最后一层会输出大小合适的结果。明文和秘钥会输入到第一个全连接层中，然后这些卷积层要学着对前一层给出的混合比特位组应用某种函数，但具体应该是哪个函数没有预先指定，而是让神经网络自己通过学习来确定。

试验是从最简单的场景开始的。Alice 要发送一个机密信息给Bob，其输入项是明文P 和秘钥K。经过处理后，Alice 输出密文C。Bob 和Eve 都会收到C 作为各自的输入项，不过Bob 的输入项比Eve 多了那个秘钥K，它们的处理结果分别用PBob 和PEve 来表示。整个过程如下图所示：

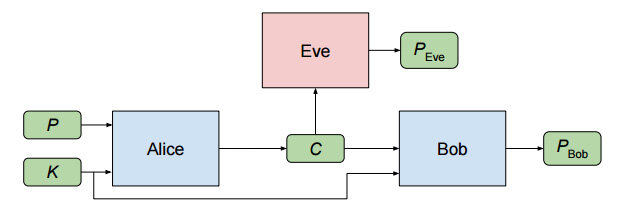
通俗地讲，Eve 的目标是从C 中准确地还原出P，换句话说就是尽量缩小PEve 跟P 的差距；Alice 和Bob 的目标是顺利地完成通信，即尽量缩小PBob 跟P 的差距，同时让Eve 无法获知他们通信的内容。目标确定之后，如果用θA、θB、θE 分别表示三个神经网络各自的参数，则可以用下面这些损失函数(Loss function) 来分别表示Eve、Bob、Alice 和Bob 的组合各自的目标：

1.Eve 的损失函数：

LE(θA,θE,P,K) = d(P,E(θE,A(θA,P,K)))

函数 d(P, P ′) = Σi=1,N |Pi − Pi′| ，即对于长度为 N 的明文 P 而言，函数 d 的结果是 Eve 得出的结果 PEve，即 E(θE,A(θA,P,K))，跟明文 P 之间各位差值的和。这个等式非常直观地表示了当明文为 P，秘钥为 K 时，Eve 的处理结果跟明文之间的差距有多大。

此外还基于明文 P 和秘钥 K 的分布取期望值定义了一个损失函数：

LE(θA,θE) = EP,K(d(P,E(θE,A(θA,P,K))))

则在损失函数的结果最小时，就得到了“最优的 Eve”：

OE(θA) = argminθE (LE(θA,θE))

2.Bob 的损失函数

Bob 的损失函数跟 Eve 的类似，也是计算从密文中重新构造出来的结果跟明文的偏差，同时扩展到了基于明文 P 和秘钥 K 的分布上：

LB(θA,θB,P,K) = d(P,B(θB,A(θA,P,K)),K)
LB(θA,θB) = EP,K(d(P,B(θB,A(θA,P,K),K)))

3.Alice 与 Bob 组合的损失函数

用 LB 减去 LE 的最优值就是 Alice 与 Bob 组合的损失函数：

LAB (θA , θB ) = LB (θA , θB ) − LE (θA , OE (θA ))

即 Alice 与 Bob 的目标是让 Bob 从密文中重新构造出来的结果跟明文的偏差尽可能小，而要让 Eve 从密文中重新构造出来的结果跟明文的偏差尽可能得大。

所以在 LAB (θA , θB ) 的结果最小时，就得到了“最优的 Alice 与 Bob”：

(OA,OB) = argmin(θA,θB)(LAB(θA,θB))

从上面设定的目标可以看出，Mart́ın 和 David 并不是分别训练 Alice 和 Bob 来学习某种已知的密码系统；而是进行联合训练，让他们成功通信并击败 Eve，但并没有预先指定达成这一目标需要使用什么密码系统。对 Alice 和 Bob 进行随机的初始化之后，就是训练神经网络从初始状态变为 (OA,OB)，或逼近 (OA,OB)。

基于随机梯度下降的训练方法，Mart́ın 和 David 用学习率为 0.0008 的 TensorFlow 的 Adam 优化器，以 256~4096 条目的小批量示例对神经网络进行训练。每对 Alice/Bob 训练一个批次，则对 Eve 训练两个批次。在明文长度为 16 位、训练条目为 4096 时得出的结果如下图所示：

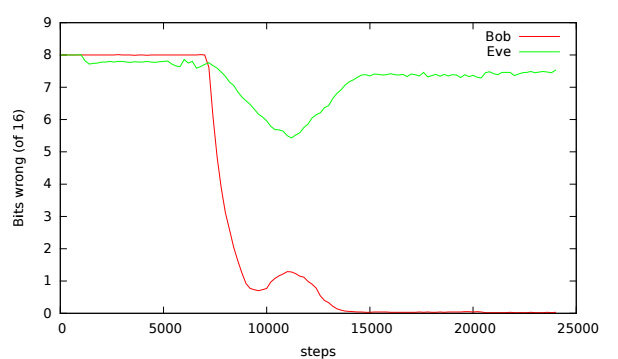
理想的结果应该是 Bob 的错误数下降到 0，而 Eve 的错误数是 8（有一半的比特位是错的）。在这个例子中，他们两个的结果一开始错误数都很高，经过一段时间后，Alice 和 Bob 的通信变得非常有效，但 Eve 的理解能力也同样得到了提升。大概在 10000 步的时候，情况开始反转，到 15000 步时，训练目标已经达成了。后续的步骤仅仅轻微增加了 Eve 的错误数。

这个训练图跟典型的神经网络训练图不太一样，结果跟步数之间的关系是动态的。这种对抗训练所呈现出来的动态变化有点儿像进化。

此外，Mart́ın 和 David 还在这个结果的基础之上研究了选择性保护的情况，即让神经网络只对一部分信息进行加密。他们的研究表明，神经网络确实能够学会如何进行安全的通信。Mart́ın 和 David 表示，接下来他们还会考虑其他任务，比如隐写术、伪随机数生成或完整性检查等。另外，神经网络不仅可用来进行加密保护信息，也能够用于攻击。 虽然看起来神经网络不太擅长密码分析，但他们在元数据和流量分析上可能会大有作为。

更详细的内容请参考他们发表的论文。

感谢冬雨对本文的审校。

给InfoQ 中文站投稿或者参与内容翻译工作，请邮件至 editors@cn.infoq.com 。也欢迎大家通过新浪微博（ @InfoQ ， @丁晓昀），微信（微信号： InfoQChina ）关注我们。