欢迎阅读新一期的内核杂谈。让我们一起继续 vector database 的学习。上一期介绍了两种 vector 的存储方式,linear storage 和 k-d tree,同时分析了这两种方式的优劣。这一期,我们将学习如何进一步提升存储和查询的效率。
Tree-based approach: ball tree
在上一期介绍 k-d tree 的缺点的时候,提到了 k-d tree 的每次二分并不是均匀的,因为它的每次二分都只考虑某个 dimension 上的数据分布。那么有什么方法可以提升二分的效率,尽可能均匀地将剩余的 vector points 分到左右子树呢?这就是我们下面要介绍的 ball tree。
Ball tree 的算法描述非常简单。下面,请所有的读者和我一起运用一下我们的空间想象能力:把所有需要被 index 的 vector 想象到一个三维空间里(真实情况是所有的 vector 会投影在更高维的 N 维空间里)。首先,想象一个球,这个球把所有的 vector 都包含在里面;然后通过这个球的中心点,找到所有 vector 离这个中心点最远的点,设为 p1;然后再在所有的 vector 里找到离 p1 最远的点,设为 p2;然后将 vector list 下面剩下的点,按照和 p1,p2 的距离远近分别划分到 p1 组和 p2 组;然后分别对 p1 组和 p2 组做递归操作,再画两个球分别把 p1 组和 p2 组的 vector 都包含进来;依次递归,直到满足 stop condition(比如深度达到某个程度,或者球里只有一个点了)。下图的示例,给出了在二维空间里面的 ball tree 构造的示例。
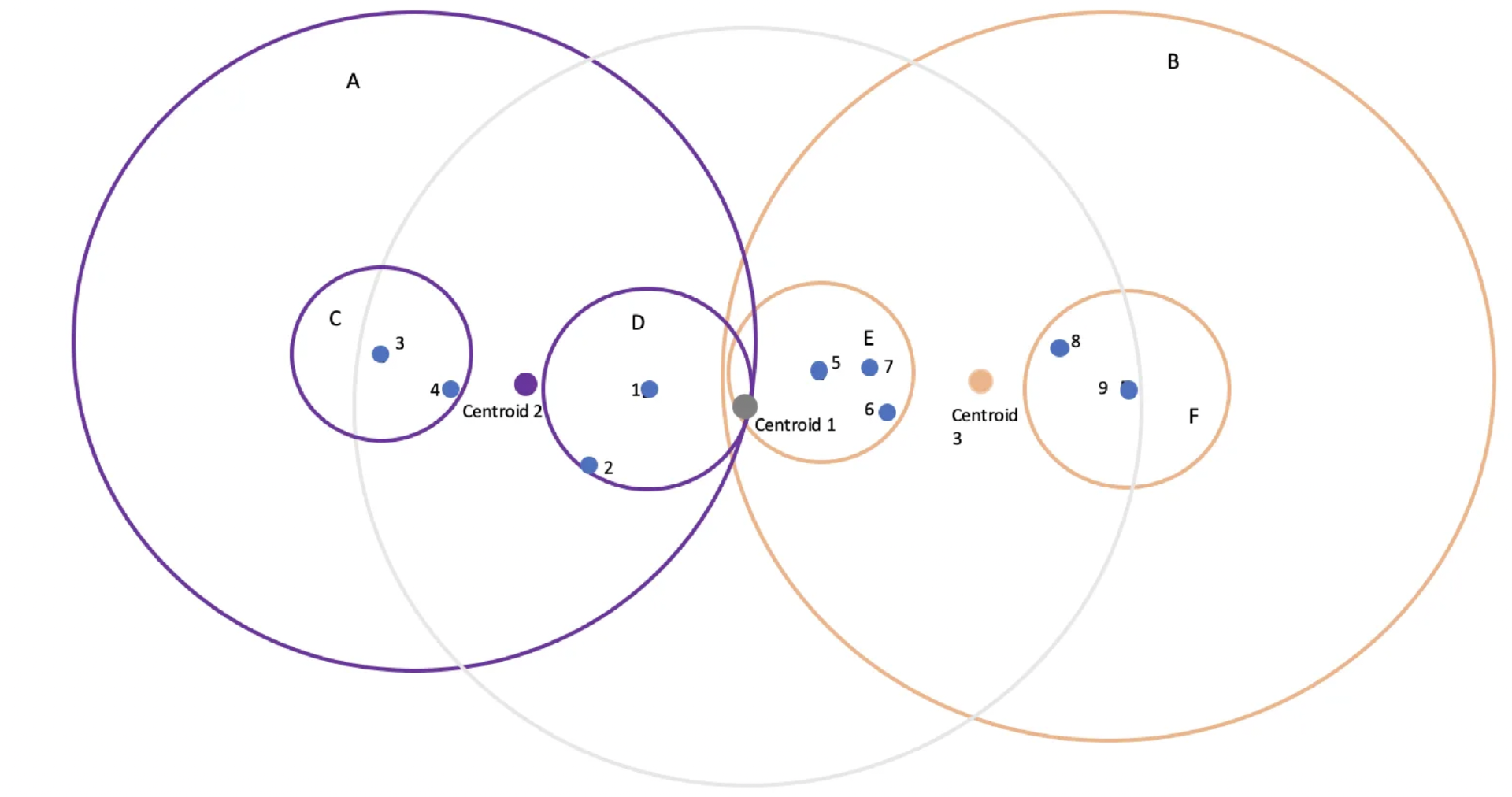
(ball tree 示例图)
如上图所示,首先通过聚类算法算出质心 1 的位置,所有的数据点(vector)围绕质心 1 形成一个圈(灰色)。从质心 1 出发,选择集群中距离最远的点,分别是点 3 和点 9。然后分别把其他的点按照和点 3 和点 9 的距离划分成两拨,然后按照聚类算法分别出计算出新的质心 2 和质心 3;以此类推。
Ball tree 的具体算法描述,如下:
1)初始化:给定一个 k 维空间中的一组 vector 开始。
2)找到质心:通过对所有的 vector 对于 k 个维度求均值,找到质心。
3)分组:在集合中找到两个点 P1 和 P2,使得 P1 和质心距离最大,再找到距离 P1 最远的点 P2。
4)划分数据:将 vector list 里的其他点指定给它最近的分组点;即创建两组点。一组离 P1 更近,另一组离 P2 更近。
5)创建子球体:对于每一组,计算所有点包围的最小球体的中心和半径。
6)递归划分:对于两组 sub-set vector,分别应用步骤 2)至 5),直至停止条件。
7)停止条件:当满足停止条件时,递归结束。这可能是当一个球体包含的点少于等于某个特定数量(比如 1 个),或者当树达到特定深度时。
Ball tree 的缺点:
ball tree 在构造二叉树的形式上,旨在做到比 k-d tree 更均匀。那 ball tree 的缺点呢?首先,由于二分法存在随机性,两个空间上接近的 vector point 理论上是可能被分在不同的子树里的。这带来的问题就是,做 similarity search 时,可能由于上层结构,导致查询返回的结果不是最优解。参考上图示例,在紫色圈里找一个点但更靠近 P5。搜索这个点时,上面的 ball tree 会返回 P1。当然,这个缺点,k-d tree 也存在。其次,ball tree 的构造比 k-d tree 更复杂, 找到质心的计算需要遍历所有在这个球体里的点来做计算。同时,由于也是 tree-based approach,插入和更新 vector 都不适用。
Tree-based Approach 总结
上期介绍的 k-d tree 和这期介绍的 ball tree,都属于 tree-based approach。基本思想都是通过将向量空间的上的点通过构造二叉树拆分来提升搜索效率。虽然在具体的构造和搜索算法上稍有不同,但优劣都是共通的,比如查询的都是近似解,以及不支持更新或插入新的 vector points。它们面临的另一个实际问题是,当 vector 的 dimension 特别大的时候(黑话叫 curse of dimensionality),整个 vector 空间会变得愈发稀疏(这里也需要一些超维空间想象能力),这使得算法很难均匀地切分左右子树。除了 k-d tree 和 ball tree,另一个非常受欢迎的 tree-based approach 是 approximate nearest neighbor oh year(ANNOY)。依然是通过构造二叉树(或者森林)来提升搜索效率,区别于 k-d tree 和 ball tree 的算法,ANNOY 使用了 random projection(下文会介绍)来做切分,通过引入随机性来解决 curse of dimensionality 的问题(这有一篇介绍 ANNOY 细节的 blog,https://zilliz.com/learn/approximate-nearest-neighbor-oh-yeah-ANNOY 推荐大家阅读来学习更多细节)。二叉树搜索的另一个问题是,当在数据量(vector points)巨大的场景下,比如 billions of points 时,搜索的速度会变慢。因为只能做二分查找,并且,由于 points 太多,树会变得非常深,对于内存使用也不是很友好。有什么方法可以进一步提升搜索效率呢?
Partition-based approach: inverted file index
在关系型数据库中,为了提升查询效率,我们通常用 B+树来建立索引,原因是 1)B+树的搜索效率更高(因为 fanout children 更多,搜索 1 亿数据,fanout 100 的话只需要 4 次查询);2)对内存更友好,把非叶节点存在内存中,支持高效索引,然后 sequential IO 来读取具体的数据。我们下面要介绍的方法:inverted file index(IVF),虽然并不是照搬了 B+ tree 的算法,但思想是类似的,即都是通过增加 fanout 来提升搜索效率。
IVF 的算法非常直观:IVF 通过将整个 vector 空间拆分成 k 个子空间,并对每个子空间找到一个代表质心(centroid)。并将子空间的所有 vector points 都 match 到这个质心上。给定一个要查询的 vector,先通过和所有的质心比较找到最近的质心,然后在这个质心所代表的子空间里搜索最近的点(可以用 linear search,也可以应用 tree-based approach 来进一步优化)。
根据给定一个 vector space 和超参 k,如何找到质心,并构建 IVF 索引呢?答案:可以应用经典的 k-means 算法来实现。下面是 k-means 的算法描述:
1)初始化:首先,确定超参 聚类数量 k。然后,通过从数据集中选择 k 个数据点随机初始化 k 个中心点。2)分配:将每个数据点分配给最近的中心点。"最近"基于数据点和中心点之间的 similarity metrics 定义来计算(通常是欧氏距离)。
3)更新中心点:通过找到分配给每个中心点的聚类中的所有数据点的平均值,计算新的中心点。本质上,是在找每个聚类中所有数据点的中心。
4)重复步骤 2 和 3:继续重复步骤 2 和 3,直到中心点的位置停止改变,或者达到最大迭代次数。当中心点不再改变时,这意味着算法已经收敛,数据点已经被分组成聚类。
5)停止条件:当中心点的位置在连续迭代中不再改变(或者变化很小)或者一旦达到预定义的迭代次数时,算法停止。
IVF 的代码实现也非常简单,下面是让 ChatGPT 生成的代码,用到了 sklearn library 里面的 kmeans 库。
from sklearn.cluster import KMeansimport numpy as npclass VectorSpaceSearch: def __init__(self, n_clusters): self.n_clusters = n_clusters self.kmeans = KMeans(n_clusters=n_clusters) self.inverted_index = {} def fit(self, X): """Fit the model to the data X and build the inverted index.""" labels = self.kmeans.fit_predict(X) for i, label in enumerate(labels): if label not in self.inverted_index: self.inverted_index[label] = [] self.inverted_index[label].append(X[i]) def search(self, query, similarity_func): """Search for the most similar vector to the query.""" label = self.kmeans.predict(query.reshape(1, -1)) cluster = self.inverted_index[label[0]] similarities = [similarity_func(query, x) for x in cluster] return cluster[np.argmax(similarities)]考虑到 IVF 也是一种 approximate 算法,即最接近的 vector 可能被分配在临近的另一个子空间里(和上面介绍的 ball tree 有类似的问题),在实际情况下,可能会同时搜索附近的子空间里提高准确率,特别是在超高维的空间下(curse of dimensionality)。
Locality Sensitive Hashing: search for cosine similarity
之前介绍的所有方法都适用于搜索高维空间上距离相邻的点(比如欧式距离)。下面,我们来介绍一个用来高效检索 cosine similarity metrics 的算法,locality sensitive hashing(LSH)。LSH 的思路和 IVF 类似,也是通过一种手段将空间上的 vector points hash 到不同的 bucket 里面,且保证同一个 bucket 里的 points 在 cosine similarity 上更相近(角度接近)。
要了解 LSH,依然需要我们发挥一下高维空间想象力。咱们一步一步来。
1)LSH 需要给定一个固定数字(say num)的 random projections,每个 random projection 就是一个和维度等长的 vector。这个 random projection 在这个高维空间中相当于一个 hyperplane(超平面),把整个高维空间一分为二。
2)DotProduct 计算:给定空间中的一个 vector,和某个 random projection 求 dot product,值是一个标量。这个标量>0 表示这个 vector 在这个超平面的一边(<0 则表示在另一边)。将这个标量用 0 或 1 表示,然后给定一个 vector 和所有的 random projections 求 dot product 就会得到 num of bits,这个 bit string 就是这个 vector 在这组 random projections 下的 hash bucket(比如当 num=8 时,一个 bit string 可以是 01101011)。
3)DotProduct 和 Cosine similarity 的关系:当两个向量在角度上接近时,它们倾向于落在随机绘制的超平面的同一侧。因此,对于这些随机超平面的投影,它们的哈希位会是相同的。这就是 LSH 与余弦相似度相结合的原因。当随机投影的超平面数量更多时(即,更长的哈希码),方向接近(根据余弦相似度)的向量会得到相同或相似的哈希码的可能性就会增加。
4)建立多组 random projections 和多个 hash 表映射:由于超平面是随机生成的,有可能它无法正确地将相似和不相似的向量分开。为了解决这个问题,使用多个哈希表(每个表都有一组不同的随机超平面)。这增加了相似向量在至少一个表的同一桶中被哈希的概率,从而提升了搜索的准确性。
有了上述的理论铺垫,可以总结出 LSH 的算法描述:
1)通过一组 random projections 将整个空间分成了 2^num 个 hash bucket,然后将不同的点通过计算 hash bits 映射到这些 bucket 里面。
2)然后给定一个要查询的 vector,计算出相应的 bucket,然后通过 linear search 来找到在这个 bucket 里 cosine similarity 最高的点。
3)提升准确率:也可以通过创建多组 random projections,将整个空间的点映射到多个 hash table 里面,找到对应每个 hash table 里 match 的 hash bits 的点的集合。通过计算 cosine similarity 找到最相似的点。
LSH 的代码实现也不复杂,下面是 ChatGPT 给出的实现示例:
import numpy as npimport collectionsclass LSH: def __init__(self, num_vectors, dim, num_hash_tables, num_hash_bits): self.num_hash_tables = num_hash_tables self.num_hash_bits = num_hash_bits self.dim = dim self.hash_tables = [collections.defaultdict(list) for _ in range(num_hash_tables)] self.rps = [np.random.randn(dim, num_hash_bits) for _ in range(num_hash_tables)] def hash(self, table_index, v): rp = self.rps[table_index] bits = v.dot(rp) > 0 return ''.join(['1' if b else '0' for b in bits]) def add(self, v, label): for i in range(self.num_hash_tables): h = self.hash(i, v) self.hash_tables[i][h].append((v, label)) def query(self, v): results = [] for i in range(self.num_hash_tables): h = self.hash(i, v) results.extend(self.hash_tables[i][h]) return results# Example usagenum_vectors = 1000dim = 300num_hash_tables = 10num_hash_bits = 16data = np.random.randn(num_vectors, dim)labels = np.arange(num_vectors)lsh = LSH(num_vectors, dim, num_hash_tables, num_hash_bits)for i in range(num_vectors): lsh.add(data[i, :], labels[i])# Get nearest neighborsquery_vector = np.random.randn(dim)results = lsh.query(query_vector)# Sort results by cosine similarityresults = sorted(results, key=lambda x: np.dot(query_vector, x[0])/(np.linalg.norm(query_vector)*np.linalg.norm(x[0])), reverse=True)# Print labels of top 5 similar vectorsfor i in range(5): print(results[i][1])总结
这期,咱们一起学习了 ball tree 的算法并总结了 tree-based approach 的优缺点。同时也介绍了两种不同类型的 partition-based approach:基于将空间划分成 K 个子空间,并建立对质心的倒排索引的 IVF 方法;以及基于 random projection 超平面划分的 locality sensitive hashing 方法。虽然两者采用了不同的方法对整个向量空间进行划分,但优化搜索的思路是一致的:即通过迅速找到一个最相近的子空间(或者子集)来提升搜索效率,然后通过 linear search 来获得准确的值。由于空间划分的不确定性,两种方法都可能返回错误的答案,因此,都提出了通过一些冗余计算来提升准确率的方法。
内核杂谈微信群和知识星球
如果觉得有收获,也愿意请我喝杯咖啡的话,可以在爱发电平台打赏我!
https://afdian.net/a/zzzgu/plan
将创作的自由还给创作者!爱发电是让创作者简单地获得稳定收入的粉丝赞助平台。无论你在创作什么,都能在这里获得持续的资金支持,让创作从此更自由。
目前我有全职工作,求打赏完全是出于可以让我分泌更多的多巴胺(任何非工作收入都算天降之财!)。重要的话说三遍:请完全出于自愿打赏(如果你是学生,请务必不要打赏)!请完全出于自愿打赏(如果你是学生,请务必不要打赏)!请完全出于自愿打赏(如果你是学生,请务必不要打赏)!
内核杂谈有个微信群,大家会在上面讨论数据库相关话题。目前群人数超过 400 人啦,所以不能分享群名片加入。可以添加我的微信(zhongxiangu)。请备注:内核杂谈。
除了数据库内核的专题 blog,我还会 push 自己分享每天看到的有趣的 IT 新闻,放在我的知识星球里(免费的,为爱发电),欢迎加入。