工业制造的智能化转型：从传统决策到运筹优化

随着工业智能化和数字化转型的深入推进，制造业企业在决策管理中面临越来越复杂的挑战。传统依赖人工经验的决策模式，已难以适应当前多品种、小批量的生产需求。在这种背景下，智能决策技术，特别是基于运筹优化和人工智能的高级计划与排程（APS）系统，逐渐成为推动企业降本增效、提升运营效率的关键工具。

在 6 月举办的 ArchSummit 全球架构师峰会上，清智优化董事长兼总经理蒙绎泽博士分享了主题演讲《企业全层级决策管理智能优化平台助力企业降本增效增收》。其详细探讨了智能决策的发展历程及其在制造业中的应用，重点介绍了运筹优化技术的理论基础、求解方法及其在实际项目中的落地应用。通过对典型案例的阐述，展示了智能优化平台如何在复杂的工业场景中发挥作用，从而为企业提供全面、优化的决策支持。

以下是演讲实录（经 InfoQ 进行不改变原意的编辑整理）。

智能决策发展历史

尽管数字化转型、工业化和智能化已经发展了很多年，但在许多制造业企业，尤其是一些领先的企业中，仍然存在许多依赖人工决策的环节。例如，在制定生产计划、采购和物流运输计划等方面，仍然存在依赖经验进行决策的现象。在当前多品种、小批量的生产方式下，人工决策不仅耗时长，而且质量也难以保证。这是因为决策空间规模和计算复杂度随着产品种类的增加而呈指数型增长。

目前，工厂基本上具备了柔性生产能力，但多种因素的叠加使得传统人工决策面临许多局限性。虽然企业已经采用了 ERP 和 MES 等系统，主要用于记录和执行流程，系统也可能包含一些基于规则的简单排产和决策逻辑，如先进先出（FIFO）等，但这些简单规则的能力非常有限，不能支持复杂的调度问题。

我们的目标是基于运筹优化技术，结合人工智能技术，全面考虑经营过程中的决策要素，实现整体最优化的解决方案，从而显著降低成本并提高效率。

APS（Advanced Planning and Scheduling，高级计划与排程）有狭义和广义之分。狭义的 APS 主要指的是车间生产计划排产，这通常包括 AP（Advanced Planning，高级计划）和 AS（Advanced Scheduling，高级排程）。我们重点聚焦于工厂内部的生产计划。广义上的 APS，其应用范围可以扩展到整个供应链管理，覆盖更广泛的功能和领域。

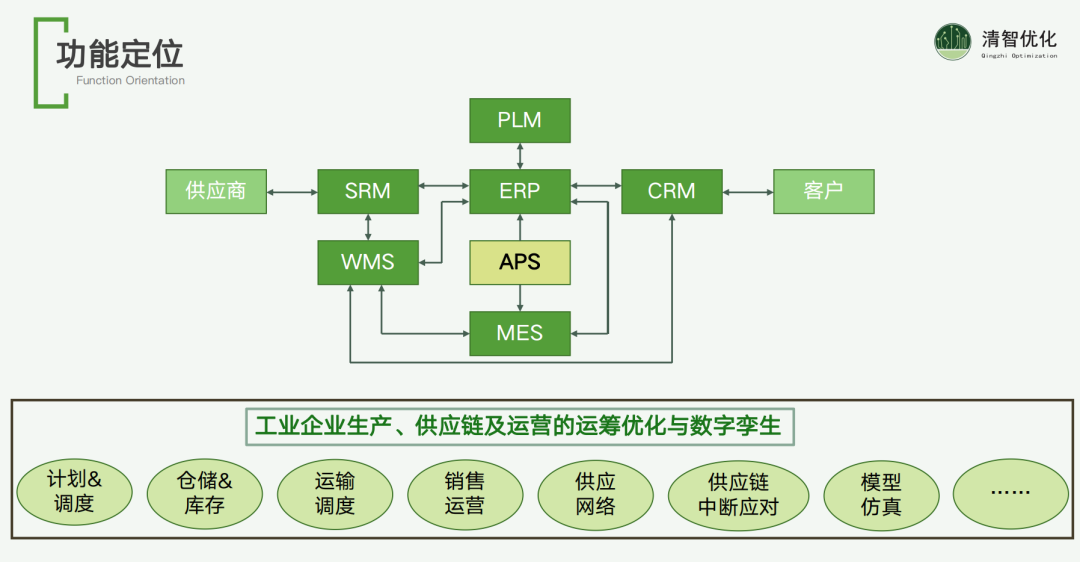
我们的定位是将 APS 视为智能工厂的大脑。在智能工厂的架构中，ERP（Enterprise Resource Planning，企业资源计划）、MES（Manufacturing Execution System，制造执行系统）、WMS（Warehouse Management System，仓库管理系统）和 CRM（Customer Relationship Management，客户关系管理）等系统主要负责数据和单据的记录。而我们的 APS 系统则是在这些系统之上，进行计划的执行。具体来说，数据从这些系统上传至 APS 后，我们会进行最优运算，生成最优细化计划，并下发执行，以替代人工计划环节。这个过程涉及到如何制定最优计划，而最优计划通常能够为客户带来显著的效益，包括计划调度、仓储库存、运输调度等场景。

关于运筹优化技术

运筹优化是一门起源于二战期间的学科。它主要研究的是如何在资源有限的系统中，利用数学优化算法来制定人力、物力和财力的最佳调配方案，目的是使整个系统的效益达到最大化。运筹优化技术涵盖了多种核心算法和技术，包括规划论中的整数规划、非线性规划、动态规划、图论、组合优化以及库存论等技术。

典型的优化问题通常包括一个优化目标以及多个约束条件。依据变量和约束条件的特点，可以将其分为四类主要的规划模型：线性规划、整数线性规划、非线性规划和混合整数非线性规划。

在这些模型中，MIP（混合整数规划）是最常用的一种。它指的是问题中的决策变量具有离散特性，同时约束条件是线性的。在实际应用中，许多不同类型的问题最后都可能被转化为 MIP 问题来求解，这是因为 MIP 模型能够在保持约束条件线性的同时，处理决策变量的离散性，从而找到最优或近似最优的解决方案。

在运筹优化领域，求解器扮演着至关重要的角色。它是一个专门用来求解规划模型的算法包。我们可以将求解器比作一个高级计算器，当我们将规划模型输入其中，它能够快速地为我们提供最优解或可行解。

求解器内部集成了多种优化算法，这些算法各具特色，能够应对不同类型的优化问题。其中，分支定界和分支定价是最典型的算法。分支定界通过系统地探索解空间的各个部分来找到最优解，而分支定价则是一种用于解决整数规划问题的有效方法。除了这些，求解器还可能包含一些启发式算法和梯度下降等数值优化方法。

解决运筹学问题通常涉及四层抽象。对于业务人员，他们接触最多的是第一层，即实际的商业问题。例如，作为工厂的总监，他们需要决定如何为工人排班，或者如何选址建立工厂设施。这些是工厂日常运营中可能面临的决策问题。

第二层是通用问题，我们需要先将问题抽象为通用性问题。这些问题可能类似于旅行商问题、最短路径问题或图着色问题。

第三层抽象是对问题的建模范例，确定它属于哪一类优化问题，比如是混合整数规划（MIP）、线性规划还是非线性规划。

第四层抽象是求解器和求解算法。所有问题最终都归结到求解层面。这包括使用不同的搜索排序技术、Benders 分解以及分支定界等方法。

运筹学项目的实施方法论通常包括以下几个关键步骤：

1. 数据初步分析，驱动算法设计：首先，我们需要收集相关的基础数据，并对其进行分析以获得初步的见解。这一步至关重要，因为现实生活中的许多问题都是 NP 难问题，直接求解可能需要很长时间。通过从数据中提取见解，我们可以简化模型求解过程，利用数据的性质来加速求解。

2. 设计和建立高效数学模型：接下来，我们需要设计和构建针对实际问题的高效数学模型。运筹学同行都知道，模型的建立有高效和低效之分，同样一个问题的不同建模方式计算效率可能天差地别。

3. 分析模型结构及难易程度：模型建立后，我们需要分析模型的结构以及解集的性质，为设计求解方法打下基础。

4. 设计求解方法：这一步涉及到选择合适的求解器、设计求解框架，决定是使用启发式算法还是精确求解，是否需要分阶段求解。求解器是一个工具，但并非万能，还需要结合其他技巧来高效求解。

5. 代码实现：将设计好的求解方法转化为代码实现，并进行初步求解，得到计划结果。

6. 数据审查和校验：对初步求解结果进行审查和校验，这可能涉及到与现场实施人员的沟通。

7. 算法性能分析：对求解算法的性能进行分析，以评估其效率和准确性。

8. 迭代优化：与现场业务人员反复确认，因为业务人员提出的需求可能并非其真正需求。通过不断展示结果，帮助他们逐渐明确真正的需求。

9. 回测对比和效益提升：进行回测对比，计算效益提升，并给出管理建议。

运筹优化模型的计算原理涉及到在求解过程中对搜索空间的逐步削减。这个过程通过不断缩小搜索范围，使得算法的上下界之间逐渐收敛。随着算法的进行，搜索空间被逐步缩小，最终收敛到一个较小的区域，从而得到一个高质量且符合要求的结果。理想情况下，这种优化算法能够达到与穷举法相同的效果，即找到最优解或近似最优解。但是，优化算法能够在较短的时间内找到高质量的解决方案，提高求解效率。

企业全层级决策管理的智能优化平台

整个智能优化平台的架构设计包括几个关键层次。首先，底层是场景和行业的模板。这些模板内置了典型行业的约束和工艺要求，例如石化行业的效益测算模型、智能配料或机加工行业的通用排程模板。

接下来，在这些模板背后，是为特定场景定制的求解器、模型库和算法模块，包括整数规划模型、启发式算法等。

最后，平台还包括数字孪生系统。这个系统允许用户对不同的方案进行手动比较，这对于实际应用中的问题解决非常关键。在实施过程中，可能会遇到现场人员质疑为什么平台会得出某个特定的解，他们可能认为自己的方案更好。面对这种情况，数字孪生系统可以让他们展示自己的方案，并计算评价指标，然后与平台的解进行比较。通过这种比较，他们往往会发现，尽管他们认为好的方案在某些方面可能更优，但在许多关键指标上却表现不佳。我们通常通过展示这些结果来说服客户，证明平台的解决方案在综合考虑多个关键指标后，能够提供更优的整体效益。

整个技术体系的底层涉及数据的获取，这些数据包括销售订单、生产订单、物流以及采购信息。这些数据通常从 ERP（企业资源计划）和 MES（制造执行系统）等系统中上传。在此基础上，我们构建了内置的优化模型，涵盖采购优化、计划排产、需求预测和经济效益优化等方面。

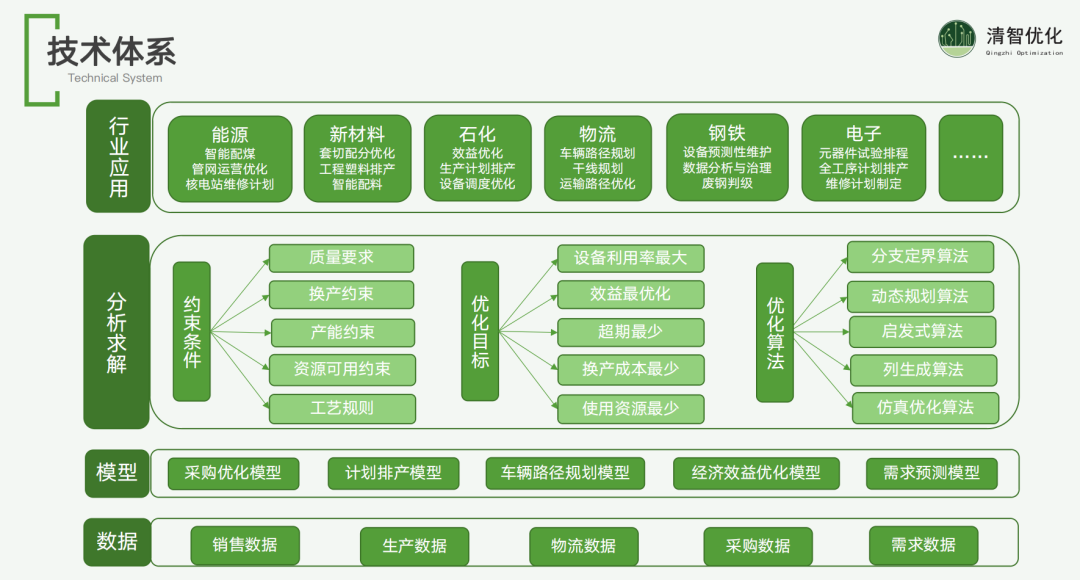
核心的分析和求解过程包括几个关键步骤。首先，需要与客户一起确定约束条件，这些条件必须是定量的，并且以白盒式的方式明确。其次，明确优化目标，比如客户最关心的 KPI 是什么，是设备利用率最大化还是成本最小化。如果存在多个目标冲突，需要设定权重，以避免不必要的争议。

优化算法的设计是我们团队的强项。我们能够为多个行业和场景提供优化解决方案。例如，在能源行业，我们可以进行管网运营优化；在新材料行业，可以进行套切配分优化和工程塑料排产；钢铁和电子行业也可以通过我们的技术进行优化。这些优化功能包括计划调度排班优化、仓储库存优化以及运输路径计算等。

典型案例一：某企业天然气管道运输优化

首先，该企业的痛点在于中国的天然气管道网络覆盖广泛，但目前主要依赖 Excel 进行管理和决策，并由人工负责每个片区，各自为政，各个链条之间没有联通。因此，需要建立一套生产、运输、销售、存储、贸易一体化的优化模型。我们需要在满足约束条件下基于稳态计算各个节点的最优参数，实现降本增效的目的。投建规划同样问题复杂，主要难点在于系统规模日趋复杂，这虽然是网络流问题，但比传统网络流要复杂得多。原因在于压缩基站本身有复杂的工艺约束，气体在管道内流动需要满足流体力学方程，因此数学求解难度呈指数级增长。

结果方面，我们搭建了天然气全业务链条的优化技术体系，研发了适用于任意拓扑结构的天然气管网优化平台，解决了常用模型难以处理低时差和温度变化的问题。我们设计了一种针对上千节点大规模管网规划的特殊凸优化松弛算法，两年内为他们节省了 20 亿元人民币，主要通过优化压缩机的控制参数，降低能耗，同时满足任意时期客户的需求，提升了整个网络的运行效率。

在建模方面，我们建立了天然气管道网络的整体运行模型。这包括流量、流向和压力等约束的建模，以及管网的网络结构建模和多级体系的融合分析。目标函数方面，涉及多目标优化。例如，有些方案侧重于能耗优化，有些侧重于效益优化，还有一些考虑路径优化或负荷优化。

由于具体的模型主要由公式组成，我们需要关注其表达的含义，从三个层面来说明。

首先是决策变量。我们计算的决策点包括各个节点、各个时间段的压力情况、供给情况；各条线路各时间段的流向流速；以及各个储气站的库存注入量和出入量等。

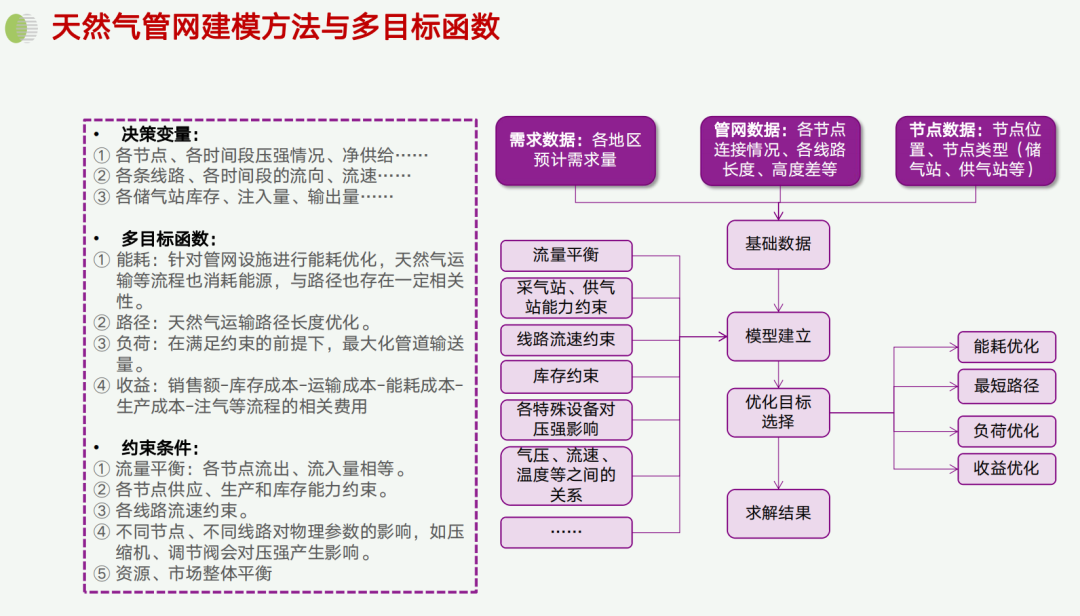
第二是优化目标。这是一个多目标函数。最主要的一层是能耗优化，例如压缩机的功率总和就是能耗。其次是运输路径优化，第三是负荷优化。还有一种目标是在满足网络所有运行约束的前提下，最大化管道输送的气量。此外，还有收益最大化的方案。收益是销售减去库存、运输能耗、生产注气等相关费用后的结果。

第三是约束条件。需要考虑流量平衡、各节点的供应生产和库存能力等约束。我们需要的数据包括各地区的预计需求量、管网的数据和节点的数据等。

针对非凸非线性可行域的快速求解模块的解过程简单介绍一下，因为算法相对复杂，具体细节可以参考相关论文。对于非凸非线性的可行域，我们的快速求解模块依靠两大核心技术：分段线性近似算法和凸优化松弛算法。这些方法可能有些复杂，我简单解释一下凸优化松弛的概念。

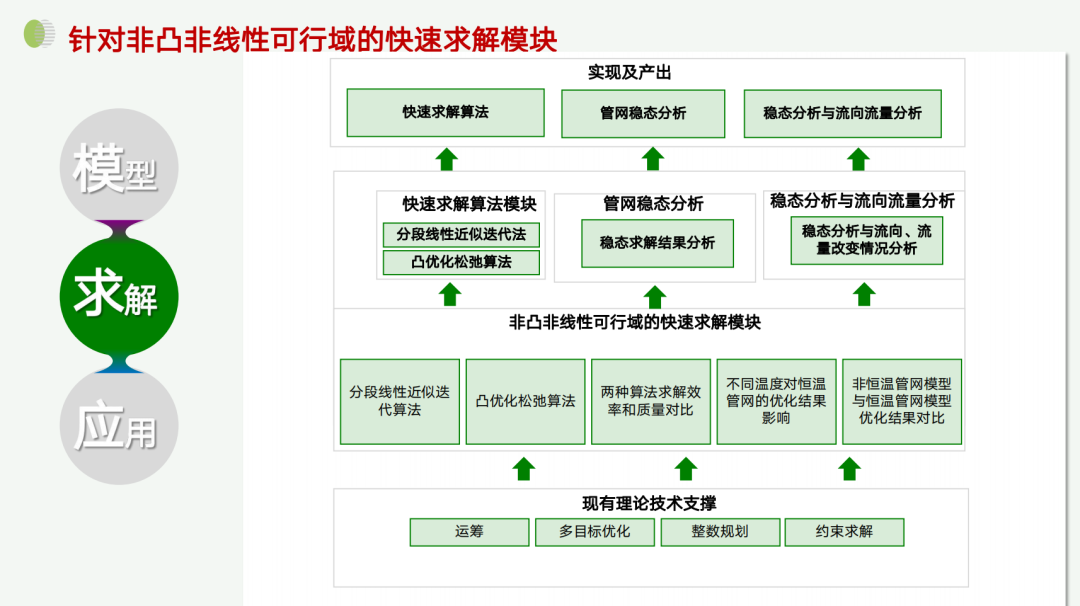
如前所述，这是一个非凸非线性的问题，主要因为包含很多平方项、开方项或分式。例如，对于一个工作的压缩机，其功耗需要通过联立不等式计算。功耗是天然气流量乘以等熵头再除以压缩机效率，这些复杂关系使得问题变得非凸非线性。优化模型需要最小化所有压缩机的总能耗，这种情况下非凸非线性问题特征明显。

所谓凸优化松弛，是将原先非凸非线性问题中的一些项进行松弛处理，使其转化为凸优化问题。虽然这会改变问题的解空间，但通过迭代框架，可以让解尽可能收敛到原问题的解。转换成凸优化问题后，求解效率和速度大大提高。

我们也进行了应对流量不确定性的一些优化，建立了鲁棒优化模型。鲁棒优化的意思是，即使在最坏情况下，你的成本仍然是可以接受的。无论流量需求有多大波动，你的系统依旧可以稳定运行。

优化模型的特点是目标函数的多层次优化，可能是双层甚至三层结构。模型类似于一个网络结构，考虑中间的需求点（如 P1、P2）会有变化。我们的决策是在知道需求会变化的情况下、如何提前做计划。这是一个非常有实践意义的问题。

我们的一些求解思路包括使用子问题动态规划重构。这是因为该问题在数学上满足一些特性，如无后效性和最优子结构特性。因此，我们对其进行了动态规划重构，以解决维度爆炸的问题。在此过程中，我们定义了一些阶段和状态转移方程。关键是我们设计了一些加速求解的近似动态规划（ADP）方法。例如，我们使用领域搜索的思维，即在动态规划中，认为相邻状态的最优决策是相似的，因此在其附近进行搜索，提高求解效率。

在应用部分，我们最终建立了一个管网运营平台，用于计算每天如何运营压缩机站和分配网络流量。该平台可以进行气源价格平衡分析、管网建设时序优化，以及 n-1 供气场景的模拟。应用成效方面，平台可以设置液体流动的属性，两年内为他们节省了 20 亿元。这主要是由于优化了能耗部分。人工决策时，每个人只负责一小部分，难以做到全局最优。通过运筹学优化后，整体的累计效应非常显著。因此，越复杂的问题，通过运筹学方法解决，效果越明显。

典型案例二：某知名烟草企业卷包排产

第二个案例是我们为某知名烟草企业进行卷包机排产优化。他们面临的行业痛点是由于过去采用单一品种大批量生产的国家计划经济模式，决策空间有限，人工制定计划相对容易。但随着市场导向转变为多品种、中小批量的柔性订单生产方式，传统的手工排产方法已无法满足企业的发展需求。其次，与大多数制造业工厂一样，他们缺乏科学完善的评估指标和方法。不同排产人员的偏好和标准不统一，评估过程模糊不清、定性评价，这不利于企业实现数字化和智能化转型。

我们应用了智能排产的五步法：1. 明确关键目标、2. 识别排产要素、3. 搭建数据基础、4. 构建排产模型、5. 评估落地验证。 通过这些步骤，我们实现了显著的经济效益指标：排产速度从数小时提升到 33 分钟内，每月换牌次数显著减少。这些优化措施每年为企业节省了 1500 万元成本。

卷包排产的业务流程大致如下：首先，营销中心会根据各个品牌的规格，提出未来两个月的货源需求计划。接着，物流中心基于这些需求，制定相应的物流发货计划。随后，公司的生产管理部门会根据这些计划，下发一个主生产计划给各个工厂，这个计划同样覆盖未来两个月的生产需求。

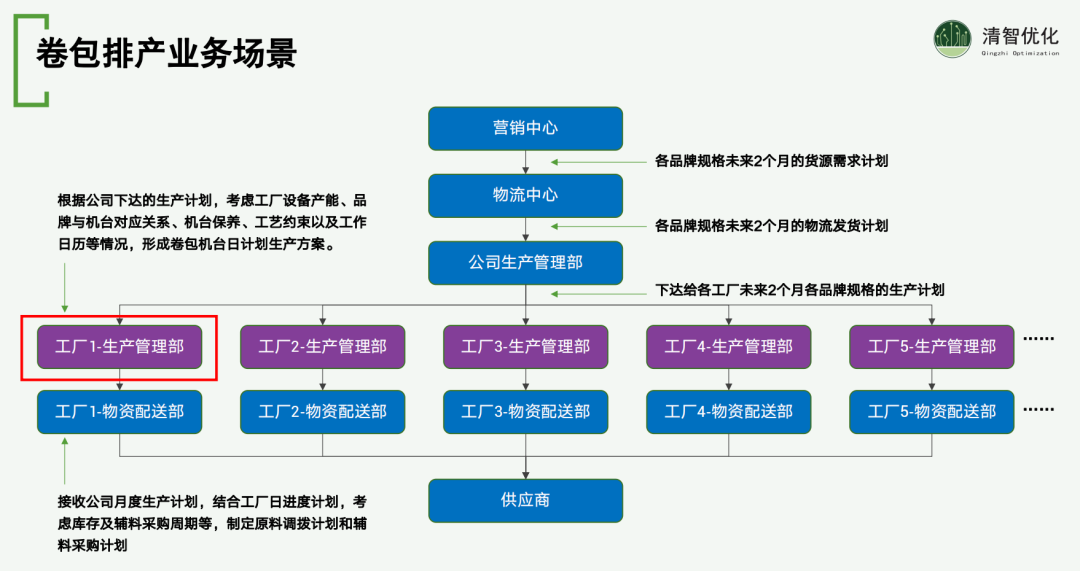
每个工厂在接到主生产计划后，会进行内部的详细规划。他们会根据粗略的生产计划，进一步考虑工厂的设备产能，包括品牌与机台的对应关系，以及工艺上的约束条件。基于这些因素，工厂会形成卷包机台的日排产生产计划方案。

最后，物资配送部在接收到这些生产计划后，会根据生产需求，制定原料调拨计划以及包括辅料在内的采购计划。

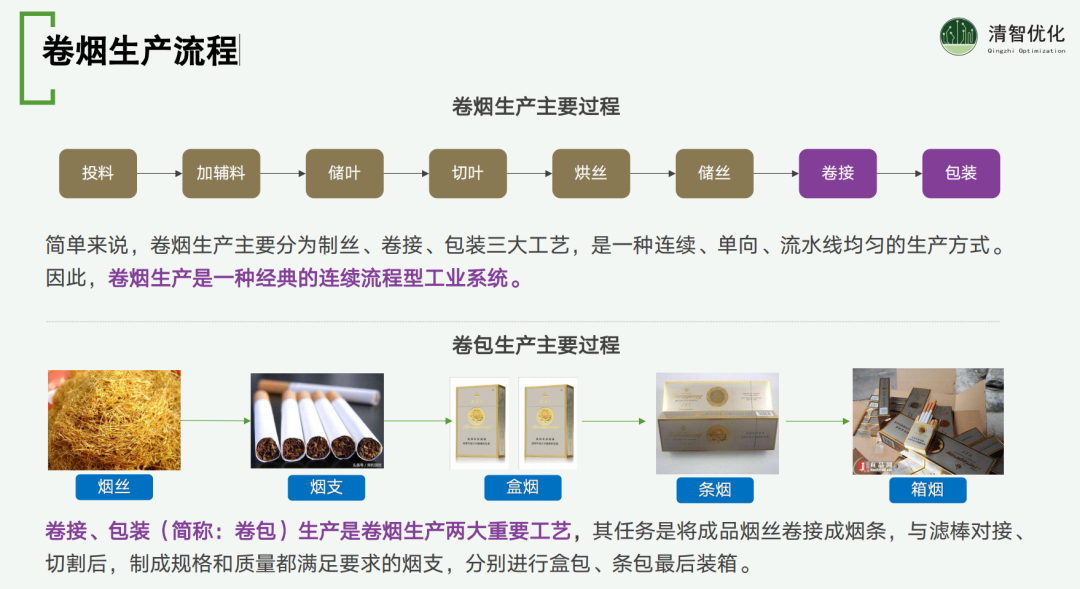
主要的生产流程包含几个核心工艺步骤，这些工艺构成了典型的连续流程型工业系统。核心工艺主要包括制丝、卷接和包装。尽管这是一个流程型的工业系统，但通过应用 APS（高级计划与排程）和优化算法，可以显著提高其效率，尤其是考虑到生产过程中多品种、小批量的特点。在这些工艺中，卷接和包装是核心环节，通常简称为"卷包"。卷接工艺的主要任务是将成品烟丝卷制成烟条，并与滤嘴进行对接。对接后的烟条经过切割，形成一定长度的卷烟。接下来是包装工艺，包括将切割好的卷烟装入小盒，然后装箱，完成整个生产流程。

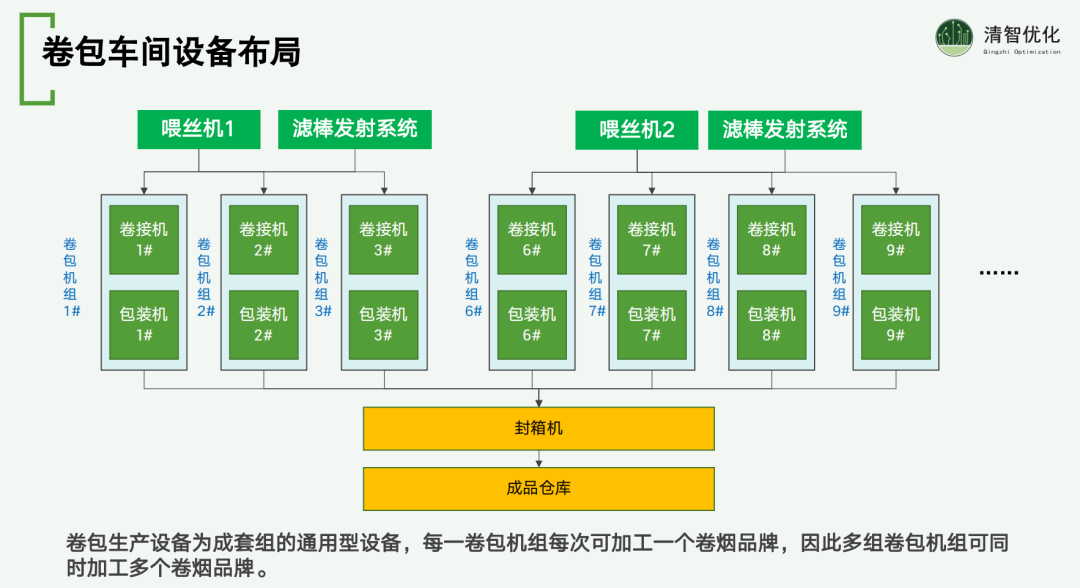
车间的设备布局体现了卷烟生产的核心流程。卷包机组由卷积机和包装机组成，它们共同完成卷烟的卷制和包装过程。在卷包机组之前，是喂丝机和滤棒发射系统，这些设备负责将烟丝和滤棒准确地送入生产线。每个卷包机组内部设计为能够一次性加工一个卷烟品牌。然而，由于车间内部署了多台机组，这些机组可以同时工作，分别加工不同的卷烟品牌。这种布局允许车间灵活地处理多品种的生产需求，同时也构成了一个典型的排程问题。

在评价指标和方法的现状总结中，我们看到公司层面和工厂层面的考虑是不同的。这两个层面在评价指标上的差异有时会导致相互冲突的行为。目前，这些指标的设定并没有一个明确和统一的标准。评价方法大多基于人工经验判断。这种基于人工经验的判断方式，是典型的制造业头部客户的画像。然而，这种方法存在一些问题：

1. 定性问题：由于依赖人工经验，评价结果往往较为定性，缺乏客观性和量化标准。

2. 各自为政：不同部门或个人可能会根据自己的理解和偏好来设定和执行评价指标，导致缺乏统一性和协调性。

工厂的卷包排产评价指标体系涵盖了多个方面，从公司角度和工厂内部角度出发，关注不同的指标。公司关注的指标举例：

1. 货源供应管理：关注货源是否供应及时准确。

2. 生产控制管理：关注生产的控制达标率，即生产是否达到既定的质量标准。

工厂关注的指标举例：

1. 生产连续性：对于流程型行业，工厂需要关注生产连续性，包括换牌时间和换牌次数。

2. 生产均衡性：工厂内部还需关注生产线的均衡运行情况，评估是否有产线长时间运行而有的产线却很少开启，以确保资源的合理分配。

3. 工作天数与设备利用率：工厂还需考虑生产计划的工作天数，以及设备的利用率。

4. 排产方式：在排产方式上，需要关注排产耗时，即完成排产所需的时间。

5. 人力资源：还需要考虑排产过程中的人力资源使用情况，如排产所需的人数。

我们建立了一套评价方法和权重体系，用于评估卷包排产的各个指标。通过层次分析法，我们确定了卷包排产的一级指标权重。例如，货源供应的权重被设定为 0.5，而生产连续性的权重则为 0.06。这些权重反映了不同指标在整体评价体系中的重要性。

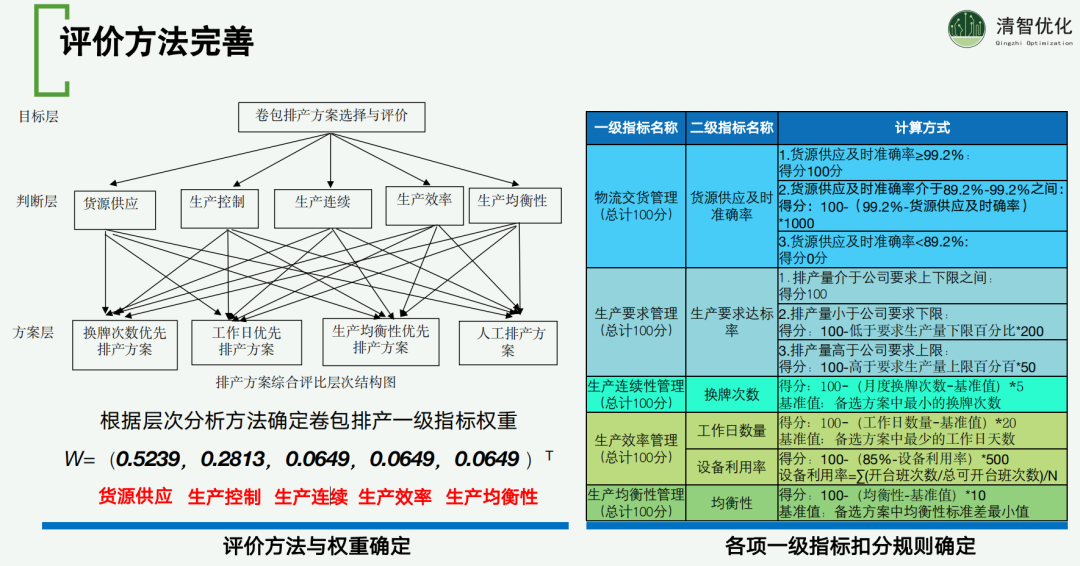
由于这是一个多目标优化问题，我们采用了层次分析法来确定权重，确保评价过程的科学性和合理性。同时，我们也制定了具体的计算方式和扣分标准，明确了什么样的表现算是达标，什么样的表现则被视为不合格。这些标准都是定量的，便于在实际评价过程中进行操作和应用。

我们首先对卷包排产的约束条件进行了整理，关注点包括产能、机组与品牌的关系、保养计划、工厂日历以及唤醒时间等关键因素。在工艺方面，我们考虑了排产的互斥关系和排产量等要素，形成了一个模型数据清单。

基于这些数据，我们构建了多目标的 MIP 模型。然而，我们发现该模型的规模相当大，直接用 Gurobi 求解需要耗费数小时，这无法满足客户对求解时间的要求。为了解决这个问题，我们采取了将规划模型与启发式算法相结合的方法。

首先，我们基于 MIP 模型获得了一个不错的初始解，但这个初始解是基于简化模型得到的，一些约束在这个阶段并未考虑。接着，我们对初始解进行了调整，比如确保批次量符合整数倍的要求，并对这些约束进行了修复。然后，我们在每个机组内部搜索换牌时间最少的生产顺序，并通过不断合并和优化，逐步改进解决方案。我们还加入了产线均衡性的补丁，以进一步提高解决方案的质量。整个求解过程的外层循环旨在避免陷入局部最优解，并减少初始解质量对最终结果的影响。内层循环则是通过算法组合来计算产量的最优分配方案。

这个项目的算法优势在于其全面性和效率。首先，算法能够考虑所有的约束条件，确保排产方案的可行性。其次，算法的排产耗时极短，单个方案的生成时间在一分钟内，这大大提高了排产的效率。同时，算法不仅考虑了所有相关因素，还能快速输出多个备选方案，以及对各个关键绩效指标（KPI）进行统计分析。

在项目实施过程中，我们经常遇到数据多元异构的问题。数据来源多样，有的来自 ERP 系统，有的是手工维护，有的通过邮件发送，还有的存储在 MES 系统中。面对这种复杂情况，我们首先制定了统一的标准。早在 2019 年，我们的项目组就参与了国家智能制造数字化模型标准的制定工作，统一了数据清单，并尽可能将数据维护在一个平台上。

在经济效益分析方面，由于企业财务成本数据未细化，我们进行了粗略估算，得出了最低节约额度。通过减少换牌次数和优化工作天数，预计每年能为企业节约 1400 多万元。

典型案例三：电子元器件高级排产

这个案例是关于电子元器件高级排产的，客户是国内领先的元器件可靠性检测机构，主要负责对电子元器件进行老炼试验，这些元器件最终将应用于国防、军工和航天领域。

该场景是一个典型的离散制造场景。客户拥有老炼设备和大量的老炼集成电路板。每天，客户需要处理数万个元器件的老炼试验，这些元器件来自不同的客户，大约有 400 多条订单。首先，客户需要进行拆单和合单的操作，决定哪些订单可以放在一起进行试验，因为它们可能有不同的试验条件，如试验温度、电流和电压等。接下来，客户需要决策如何在集成电路板上排布这些元器件，以及如何将它们放置在老炼板上。老炼板背后有电源控制，存在一些复杂约束，例如相邻区位的电压差不能超过 5 伏，但同一设备内的温度必须相同，而电压可以不同。由于可能的排列组合数量很大，排产过程非常复杂。客户一次排产需要输出一个月的计划，考虑到试验跨度较长，这进一步增加了排产的难度。

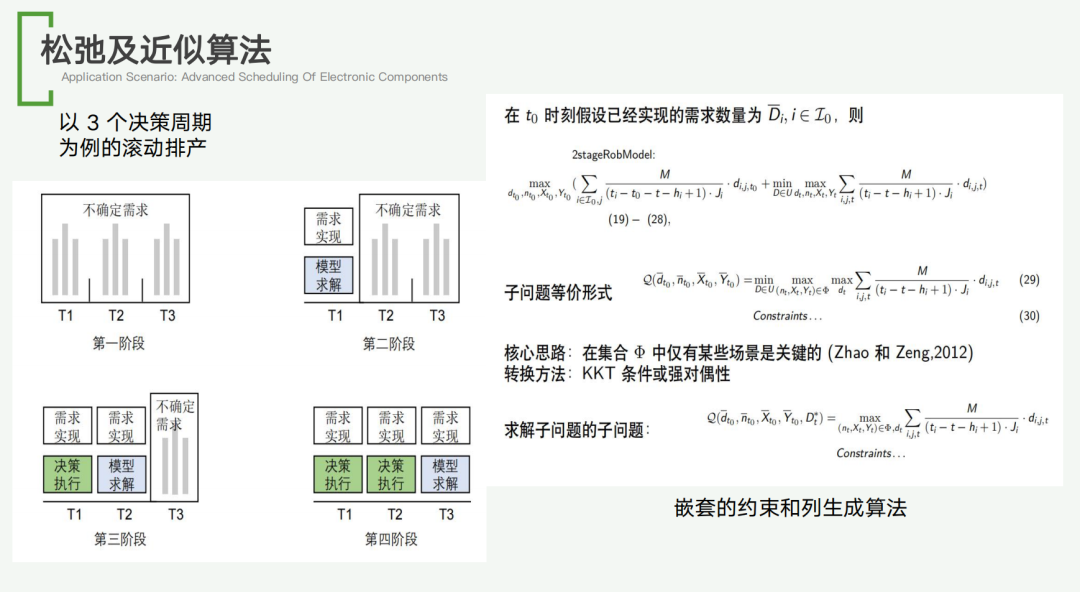
在算法设计方面，我们采用了一种在不牺牲最优解质量的前提下，寻求近似最优解的方法。这种方法可以视为多阶段拆分，将整个排产问题分解成若干个小阶段来处理。在每个阶段中，模型会考虑一系列约束条件，包括订单分配的总量上限、可用资源的约束以及工艺约束等。

我们采用的松弛和近似算法，基于滚动排产模式。在这种模式下，只知道当天的需求，而未来的需求会存在不确定性。为了应对这种不确定性，我们在算法中加入了鲁棒优化的元素，以增强排产计划的适应性和稳定性。此外，我们的算法是一个嵌套算法，利用了 KKT（Karush-Kuhn-Tucker）条件和强对偶性理论。通过这些数学工具，我们将原始问题转化为一个更易于求解的形式。这样，即便在面对复杂约束和不确定性时，我们也能够找到一个可行且近似最优的排产方案。

排产流程的核心优势在于其能够计算多个方案，并且能够根据实际情况每天进行调整。我们特别将这个流程与人工排产进行了对比，以评估其效果。通过对比过去三个月的数据，我们发现在器件总量上，a 室的生产量增加了 7%，而 b 室的生产量增加了 20%。如果考虑到单价的差异，换算成货币价值后，每个室每年可以增加 1,000 多万的效益。这一效益的增加主要是因为单位时间内能够试验的器件数量得到了提升，从而提高了整体的生产效率。通过优化排产，我们将将超期任务的器件数量减少了接近 100%。这展示了基于算法决策的魅力：算法不仅能够满足所有约束条件，还能在关键指标上实现最优解。

嘉宾介绍

蒙绎泽，清智优化创始人，教授级高工、正高级职称，工信部工业互联网创新发展工程项目课题负责人，本科及博士毕业于清华大学，香港大学博士后，上榜胡润 U30 中国创业先锋、中关村 U30、“科创中国”青年创业榜单—天津 U30、创业邦 30 Under30+ 创业先锋榜，入选天津市创业领军人才。

曾承担工信部工业互联网创新发展工程项目子课题建设，搭建了跨行业跨领域的集成供应链机理智能决策模型库，对跨行业跨领域跨区域精智工业互联网平台的有效性进行了全面试验测试，并且在冶金、化工、能源、机加工、装备制造等行业完成了应用推广验证。负责多个工业智能项目及工业大脑产品的算法设计和代码实现，落地数十个项目，成果显著。