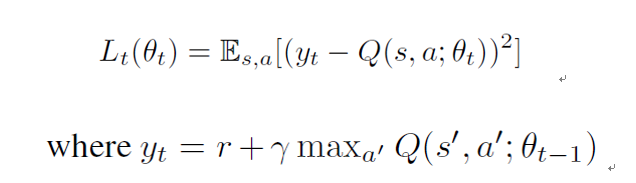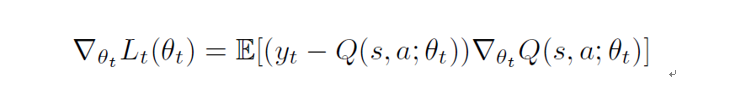【AAAI Oral】利用 DeepMind 的 DQN 解数学应用题，准确率提升 15%

研究背景

自动求解数学应用题（MWP）的研究历史可追溯到 20 世纪 60 年代，并且最近几年继续吸引着研究者的关注。自动求解应用数学题首先将人类可读懂的句子映射成机器可理解的逻辑形式，然后进行推理。该过程不能简单地通过模式匹配或端对端分类技术解决，因此，设计具有语义理解和推理能力的应用数学题自动求解器已成为通向通用人工智能之路中不可缺少的一步。

对于数学应用题求解器来说，给定一个数学应用题文本，不能简单的通过如文本问答的方式端到端的来训练，从而直接得到求解答案，而需要通过文本的处理和数字的推理，得到其求解表达式，从而计算得到答案。因此，该任务不仅仅涉及到对文本的深入理解，还需要求解器具有很强的逻辑推理能力，这也是自然语言理解研究中的难点和重点。

近几年，研究者们从不同的角度设计算法，编写求解系统，来尝试自动求解数学应用题，主要包括基于模板的方法，基于统计的方法，基于表达式树的方法，以及基于深度学习生成模型的方法。目前，求解数学应用题相关领域，面临训练数据集还不够多，求解算法鲁棒性不强，求解效率不高，求解效果不好等多种问题。由于数学题本身需要自然语言有足够的理解，对数字，语义，常识有极强的推理能力，然而大部分求解方法又受到人工干预较多，通用性不强，并且随着数据复杂度的增加，大部分算法求解效果急剧下降，因此设计一个求解效率和效果上均有不错表现的自动求解器，是既困难又非常重要的。

相关工作

算术应用题求解器：

作为早期的尝试，基于动词分类，状态转移推理的方法，只能解决加减问题。为了提高求解能力，基于标签的方法，设计了大量映射规则，把变量，数字映射成逻辑表达式，从而进行推理。由于人工干预过多，其扩展困难。

基于表达式树的方法，尝试识别相关数字，并对数字对之间进行运算符的分类，自底向上构建可以求解的表达式树。除此之外，会考虑一些比率单位等等的限制，来进一步保证构建的表达式的正确性。基于等式树的方法，采用了一个更暴力的方法，通过整数线性规划，枚举所有可能的等式树。基于树的方法，都面临着随着数字的个数的增减，求解空间呈指数性增加。

方程组应用题求解器：

对于方程组应用题的求解，目前主要是基于模板的方法。该需要将文本分类为预定义的方程组模板，通过人工特征来推断未知插槽的排列组合，把识别出来的数字和相关的名词单元在插槽中进行填充。基于模板的方法对数据的依赖性较高，当同一模板对应的题目数量减少，或者模板的复杂性增加时，这种方法的性能将急剧下降。

本文的主要贡献如下：

1. 第一个尝试使用深度增强学习来设计一个通用的数学应用题自动求解框架
2. 针对应用题场景，设计了深度 Q 网络相应的状态，动作，奖励函数，和网络结构。
3. 在主要的算术应用题数据集上验证了本文提出的方法，在求解效率和求解效果上都取得了较好的结果。

方案介绍

基于深度 Q 网络的数学应用题求解器

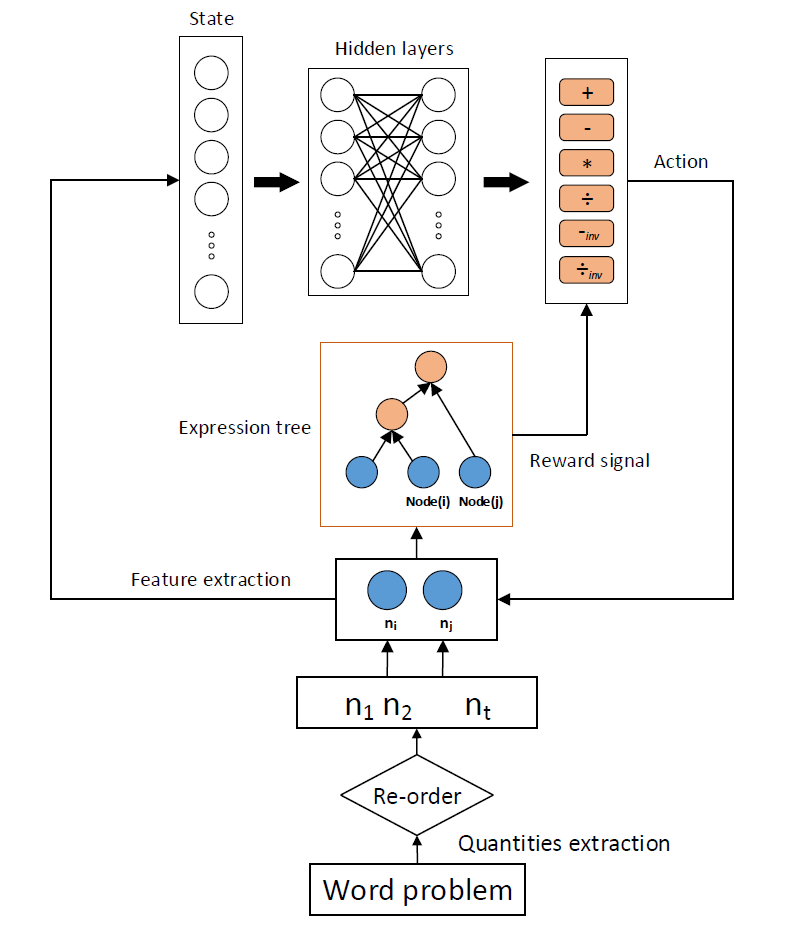
本文提出的框架如上图所示。给出一个数学应用题，首先采用数字模式提取用于构建表达式树的相关数字，然后根据重排序制定的规则，对提取出来的相关数字进行顺序调整，比如对于“3+4*5”, 我们希望优先计算 4*5，这里的数字 5，对应的文本段是“5 元每小时”，显然这里的数字“5”的单位是“元 / 小时”，当数字“4”的单位是“小时”，数字“3”的单位是“元”，遇到这种情况，调整 4 和 5 放到数字序列的最前面，随后，用已排好序的数字序列自底向上的构建表达式树。首先，根据数字“4”和数字“5”各自的信息，相互之间的信息，以及与问题的关系，提取相应的特征作为增强学习组件中的状态。然后，将此特征向量作为深度 Q 网络中前向神经网络的输入，得到“+”，“-”，反向“-”，“*”，“/“，反向”/“六种动作的 Q 值，根据 epsilon-greedy 选择合适的操作符作为当前的动作，数字”4“和”5“根据当前采取的动作，开始构建表达式树。下一步，再根据数字”4“和数字”3“，或者数字”5“和数字“3”，重复上一步的过程，把运算符数字的最小公共元祖来构建表达式树。直到没有多余相关数字，建树结束。随后将详细介绍深度 Q 网络的各个部件的设计方式。

状态：
对于当前的数字对，根据数字模式，提取单个数字，数字对之间，问题相关的三类特征，以及这两个数字是否已经参与表达式树的构建，作为当前的状态。其中，单个数字，数字对，问题相关这三类特征，有助于网络选择正确的运算符作为当前的动作；数字是否参与已经参与表达式树的构建，暗示着当前数字对在当前表达式树所处的层次位置。

动作：
因为本文处理的是简单的算术应用题，所以只考虑，加减乘除四则运算。在构建树的过程中，对于加法和乘法，两个数字之间不同的数字顺序将不影响计算结果，但是减法和除法不同的顺序将导致不同的结果。由于，我们实现确定好数字的顺序，所以添加反向减法和反向除法这两个操作是非常有必要的。因此，总共加减乘除，反向减法和除法 6 种运算符作为深度 Q 网络需要学习的动作。

奖励函数：
在训练阶段，深度 Q 网络根据当前两个数字，选择正确的动作，得到正确的运算符，环境就反馈一个正值作为奖励，否则反馈一个负值作为惩罚。

参数学习：
本文采用了一个两层的前向神经网络用于深度 Q 网络计算期望的 Q 值。网络的参数θ将根据环境反馈的奖励函数来更新学习。本文使用经验重放存储器来存储状态之间的转移，并从经验重放存储器中批量采样 (s,a,s’,r)，用于更新网络参数θ。模型的损失函数如下：

利用损失函数的梯度值来更新参数，来缩小预测的 Q 值和期望的目标 Q 值的差距，公式如下：

算法流程如下：

实验

本文采用了 AI2, IL,CC 这三个算术应用题数据集进行实验。其中 AI2 有 395 道题目，题目中含有不相关的数字，只涉及加减法。IL 有 562 道题目，题目中含有不相关的数字，只涉及加减乘除单步运算；CC 有 600 道题，题目中不含有不相关的数字，涉及加减乘除的两步运算。

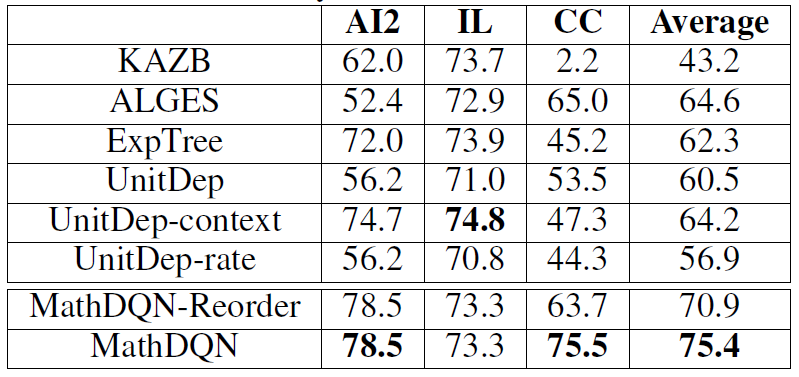
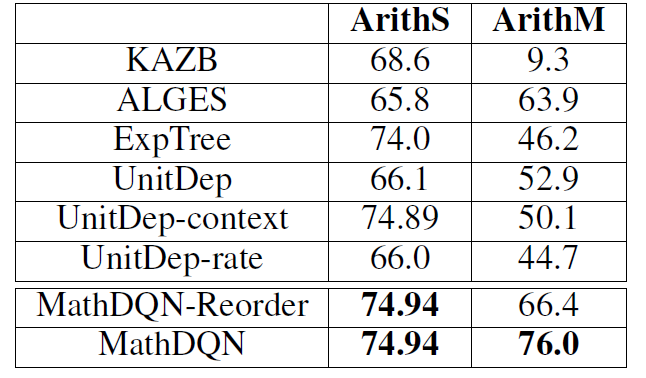
三个数据集准确率如下图：

观察上述实验结果发现，本文提出的方法在 AI2，CC 数据集上取得了最好的效果。ALGES 在 IL 上表现很好，但是在 AI2 和 CC 数据集上表现却很差，这从侧面证明了我们的方法有更好的通用性。UnitDep 提出的单位依赖图对只有加减运算的 AI2 数据集没有明显的效果，其增加的 Context 特征在 CC 数据集上有取得了明显的效果，但是却在 AI2 数据集上效果明显下降，这里表现出人工特征的局限性。对于本文提出的方法，重排序在 CC 数据集上，提升效果明显，由于 AI2 只有加减运算，IL 只涉及单步运算，所以在这两个数据集上效果不变。

除此之外，本文还做了单步和多步的断点分析，实验效果表明，本文提出的方法在多步上表现十分优异，实验结果如下图：

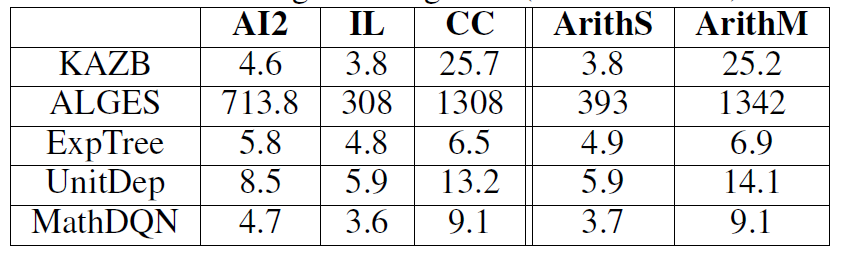
运行时间如下图：

观察单个题目求解需要的时间，我们可以发现，多步运算的数据集 CC，在时间上明显耗费更多。ALGES 由于要枚举所有可能的候选树，因此耗费时间最长。本文提出的方法，求解效率仅次于只有 SVM 做运算符，和相关数字分类的 ExpTree。

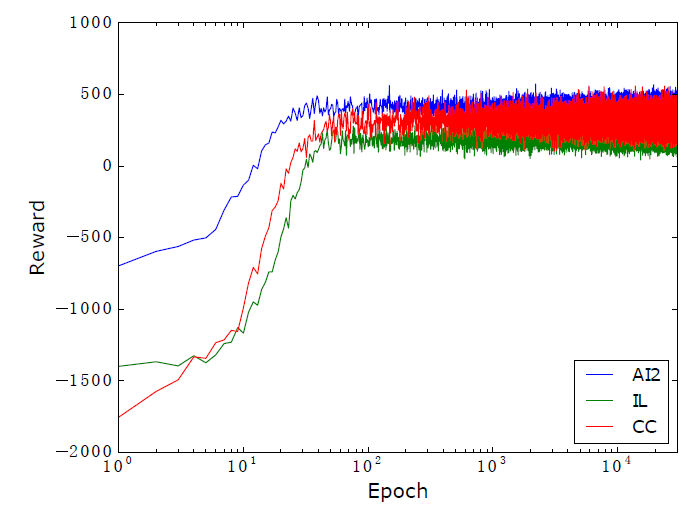
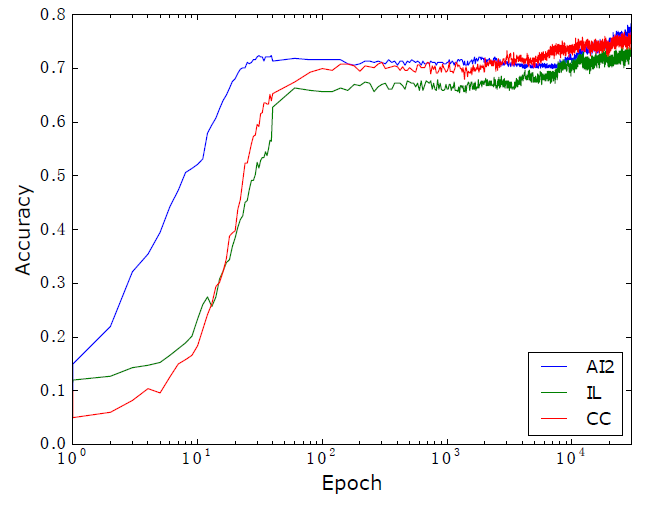
平均奖励和准确率的走势如下图：

总结

本文首次提出了一个用于求解数学应用题的增强学习框架，在基准数据上其求解效率和求解效果展现出较好的效果。

未来，我们将继续沿着深度学习，增强学习这条线去设计数学应用题自动求解器，来避免过多的人工特征。同时在更大更多样化的数据集上，尝试求解方程组应用题。

论文题目:《MathDQN: 利用深度增强学习求解算术应用题》

英文:《MathDQN: Solving ArithmeticWord Problems via Deep Reinforcement Learning》

Paper URL: http://cfm.uestc.edu.cn/~zhangdongxiang/papers/mathdqn.pdf

团队：阿凡题研究院、电子科技大学、北京大学

作者：王磊，张东祥，高联丽，宋井宽，郭龙，申恒涛