干货 | 10 分钟给上万客服排好班，携程大规模客服排班算法实践

一、背景

客户服务部门是携程以服务质量赢得客户信赖的基石，其拥有上万名一线的客服，每天进线量巨大；且伴随着业务量的起伏，每一周甚至每一天的不同时段都有需求量上的巨大变化。

如何在各个时段满足客户服务指标，同时尽量提高客服的工作体验，提升整体工作效率？这里自然而然就产生了对智能排班的需求。排班问题的核心是用更少的客服资源，既保证用户的服务质量，又尽可能保障客服班次体验。在这样的背景下，今天我们要探讨的排班算法就成了优化服务质量与成本的一个重要课题。

二、应用效果

携程的客服团队历史悠久，在很长一段时期里，排班使用人工调整的方式，已经形成了一整套完整的更新流程。但是各个部门的逻辑又有很大的区别，比如欧洲的客服需要核对时区的变化；有些部门以人为单位排班，而有些部门的管理架构要加一层小组的概念来排班。这些不同的逻辑和概念，是为了更好的管理和协调整个服务部门的资源，在携程几十年的历史中发挥了重要的作用。但也为算法的落地带来了大量不一的约束。

现在智能排班已经为携程的多个部门提供班表生成服务，在十分钟内提供优质的班表，并且符合各部门各个工种对不同工作场景的约束需求。

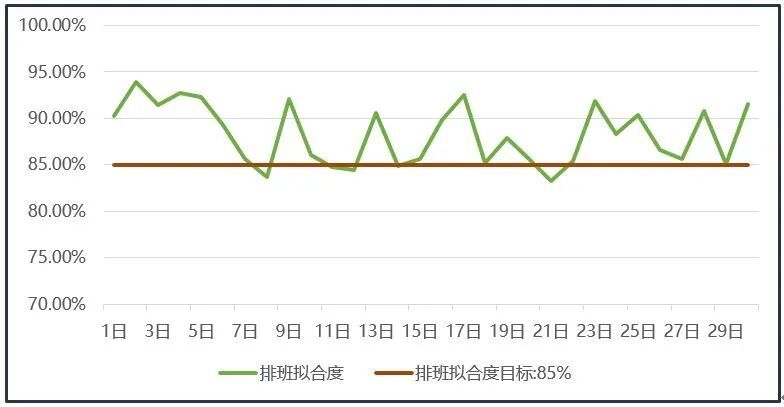
某段指定时期的验证数据

三、问题分析

排班问题，实际上就是一个带大量软硬约束的超大规模最优化问题。这是一个整数规划问题，这类问题一般都是 NP 难的。

解决这类问题，传统的方法有：

1）精确算法，主要有割平面法，分支定界法。这类算法解决的问题有一些特点：一般针对的问题规模都较小；优势是求解出来的必定是最优解。不过我们遇到的问题规模极其庞大，此方法的效率太低，无法满足业务需求。

2）近似算法，根据问题使用一些技巧自己设计出来。需要给出算法的近似比，复杂度分析，具有很强的推理能力。这类算法放弃获得最优解，提升了一些性能，不过同 1 一样，这类算法所能求解的问题规模依然比较受限制。在我们这个场景下，问题规模依然过于庞大，无法满足业务需求。

3）启发式算法，和前两种算法相比，启发式算法没有足够严格的理论分析，是算法设计者们根据经验或者观察性质设计出来的。没有严格的理论分析，通过启发式算法获得解，我们无法知道其是否是最优解，甚至无法精确得到其离最优解还有多远的距离，但是其性能上的优势十分明显，即使我们这种大规模的问题，也可以在数十分钟内获得非常令人满意的结果。

由于携程客服数以万计，再加上数十种基本班次，整体问题规模十分庞大。传统方法在可接受的时间范围内无法给出可接受的解。因此我们最终选择了启发式算法来解决问题。

针对这类启发式优化问题，问题的建模是个十分重要的步骤，这一步的好坏将直接决定问题最终的解决效果。

3.1 Nurse Rostering Problem

遇到问题，首先想要找类似的问题。我们找到了一个有一些相似的护士排班问题（Nurse Rostering Problem，后文简称 NRP），NRP 可以很好地帮助我们理解问题。

护士排班问题是说在给定的时间内为特定的一组护士安排班次，并使该排班方案满足各种硬性约束条件，同时尽量满足各种软性约束条件。但为了方便后续理解，这里以 the International Nurse Rostering Competition 2010 的规则为例，简要介绍一下这个问题，这部分规则约束十分核心。

NRP 问题的核心约束分软硬两类：

硬约束：

• 班次全部分配：每个班次都需要分配给一名员工。

• 班次不能冲突：员工每天只能轮班一次。

软约束：

这些约束实际情况中经常违反，因此这里决定将这些约束定义为软约束。

工作感受约束：

• 班次分配范围分配：每位员工需要工作超过 a 个班次且少于 b 个班次（取决于合同或约定）。

• 连续工作天数：每位员工需要连续工作 c 至 d 天（取决于合同或约定）。

• 连续休息天数：每位员工需能连续休息 e 到 f 天（取决于合同或约定）。

• 连续工作周末数：每位员工可以连续工作的周末数在 g 到 h 间（取决于合同或约定）。

• 尽量保持周末完整：员工如果需要在周末上班，那就周末两天都值班，放休就要尽量两天都放休。

• 周末上班班次一致：同一个员工在周末两天都上班的情况下，周末班次尽量保持一致。

• 不人性化的排班模式：尽量避免前后班次间隔时间太短，或连续上太辛苦的班次。例如：第一天上晚班，第二天接着上早班；或者连续上 3 天早晚班。

员工对班次的一些临时期望：

• 要求安排班次：某位员工想在指定的一天进行工作，尽量不要放休。

• 希望放休：某位员工指定某一天希望能给其放休，不要安排班次。

• 希望指定班次：员工希望能分配给其特定的班次。

• 希望避免班次：员工不希望被分配到特定的班次。

技能要求：尽量安排上班的护士已熟练掌握该班次所需的技能。

看完约束，NRP 问题的描述就很明了了。即在数值化定义好各个约束的重要性后，在尽量平衡所有约束的情况下，不停调整班表，获得最好的排班。

如下图，是一个最为简单的调整示例：

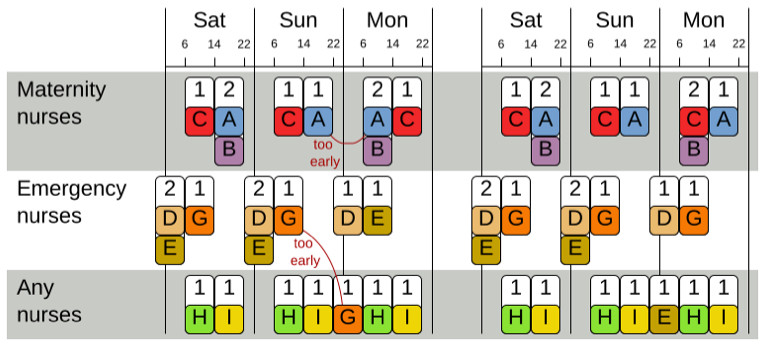
而最终的目标是得到一份最终班表，表示所有护士每天的班次安排。要注意在 NRP 问题中，调整的最小颗粒度是班次，这里将引出携程客服排班问题和 NRP 问题的最大不同。

3.2 携程集团客服排班

如开篇所述，携程的业务量每天都有着巨大的变化，加之我们的用户电话进线等待时间按秒计算，为了保证服务质量，对业务的控制需要细化到 15 分钟级别，才能保证服务质量，给用户带来最好的客服体验。

因此我们无法像 NRP 问题将排班简化为一天 3 个班次，而是细化到每天 96 个时段。由于整体安排的颗粒度细化到分钟级，就不能再仅仅安排班次，需要提高一个维度，额外计算员工的会议，休息，加班，放休等对每分钟业务量和应答量的影响。这导致整个问题复杂程度成指数级上升。

而且现实中的核心约束远比 NRP 复杂地多，总共近百条各种规则约束，对约束设计也提出了挑战。

约束设计需要数值化，但是数十上百的约束，两两之间的比例关系要恰当。这就要求数千的比例关系都要详细论证并且恰当，才能得到最终合适的班表，如若不然，很容易导致约束失衡，最终导致班表的不可用。比如，如果我们设计不合理，可能在业务量无法满足的基础上，安排部分员工超时加班，这将导致这部分员工的工作体验极差；或者在不需要的情况下，安排员工进行意义很小的加班，导致人员的浪费。

货币化约束设计     

约束的数值化设计是问题的重点，但是问题的复杂性导致整个约束设计几乎非人力可为。

针对这一问题，我们提出了一种货币化的思路。所谓货币化，就是将单独的分数设计转换为一种标准分值（在这个场景下就类似于货币），统一货币化后，我们就可以直接将约束进行对比。

很多约束是天然可以货币化的，比如加班成本、津贴等等。余下无法天然货币化的部分，积极沟通，从业务角度给出一个初始的设计，再在算法使用中做微调，即可得到可用的约束设计与最终结果。

四、建模与设计

4.1 基础结构

如前所述，排班问题是一个超大规模的优化问题，解决这种问题我们选用启发式算法。根据以往经验，用启发式算法解决现实复杂问题的时候，最核心的是对问题进行建模，模型建立的好坏将直接决定后续系统的整体效果。

客服排班实际上就是要安排员工在每个时间段的工作状态（可能包括工作，休息，开会，加班等等），以及每个时段员工所做的技能工种。

因此，我们先抽象出一个最基础的模型，包含三个维度：员工，工种以及时间，这样就形成了一个三维度的空间。

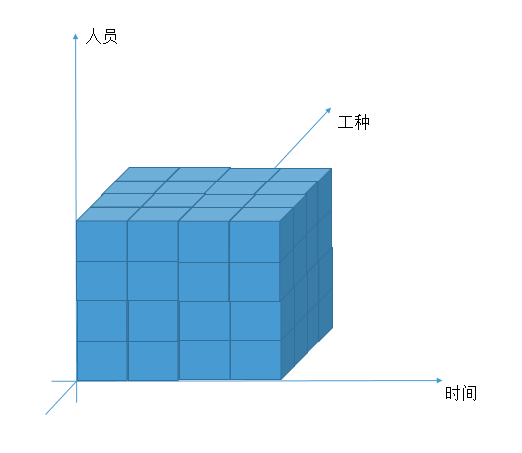
三维空间中的每一块就是最小的工作状态安排单元

如上图所示，在这个模型下我们的目标就是填满整个空间，在尽量满足约束条件的情况下，给每个最小单元安排上工作状态（工作，下班，休息等），这样就获得了班表。

这样的结果逻辑上可行，但实际呢？

4.2 结构优化

我们先不考虑吃饭，开会等等复杂的设定条件，简单设定每个最小单元的工作状态为三种：工作，下班，休息。

按照基本结构直接进行排班是否可行呢？答案是肯定的。只需要通过算法调整每个最小单元的状态，在这三种状态中选择一个，然后设定合理的约束条件就能开始跑起来了，理论上也可以得到我们想要的结果。

不过设定好一切你会发现，根本得不到一个优秀的解，甚至一个合法的解都很难得到。这是因为按照这个模型去启发式搜索，搜索空间太广。我们可以简单算一下，设排班人数为 100 人，有 2 种不同的工种可以安排，安排一周的班次，时间颗粒度为 30 分钟。

围棋一共个 19×19=361 点，每个点由 3 种状态（黑，白，空），而真实情况远比这假设要复杂的多，整个问题的复杂度也是指数上升，无法算出合适的结果。

因此需要在基础结构上做一些优化，加一层结构。首先，变量由每个最小时间单元改为工作区间，设上班时间都是整点，那一天最多 24 个班次，加上本休不上班，一共 25 种可能。休息开会等可以抽象为上班时间内的整点“中断”，这样整体复杂度可以下降为大约：

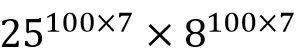
，这样总体看起来就是一个可解决的问题了。

五、算法流程

在有了模型的前提下，需要做一些算法选择与流程设计。我们首先做了一些基准测试，然后对整个算法流程做一个统一的规划与设计。

5.1 基准测试

我们获取了一个简化的业务场景，保存下来后，以此为基准搭建了一个基准测试。

首先测试了常见的算法，包括：FirstFit，Hill Climbing，Tabu Search，Late Acceptance，Great Deluge，Simulated Annealing。

以下是几个算法的部分测试结果：

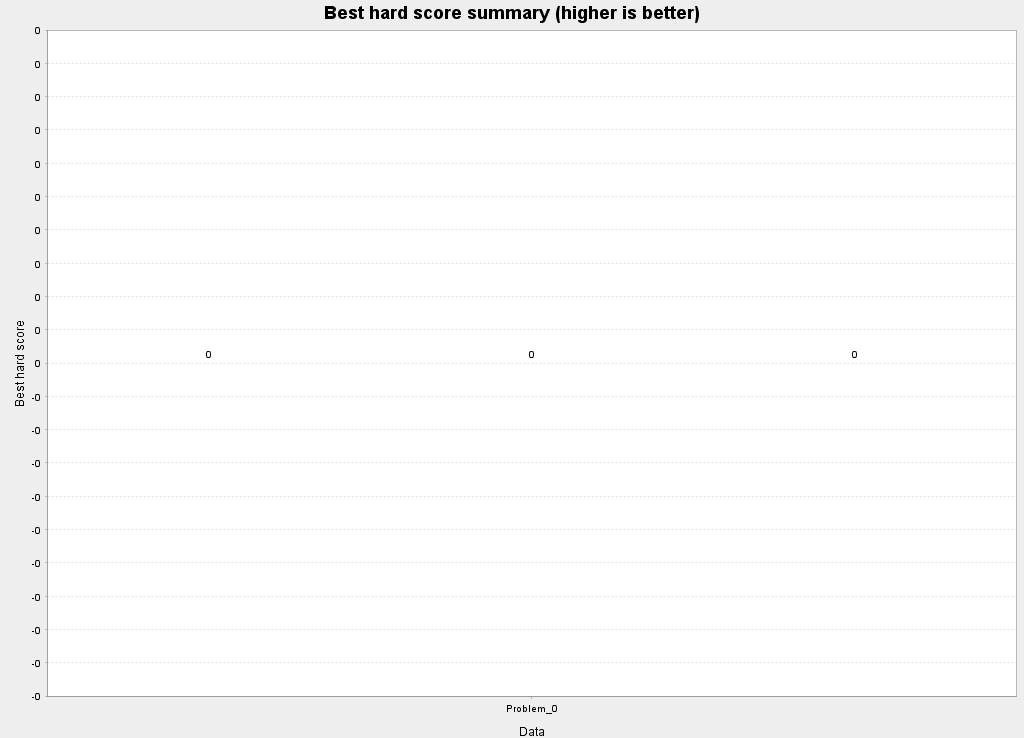
硬约束结果对比

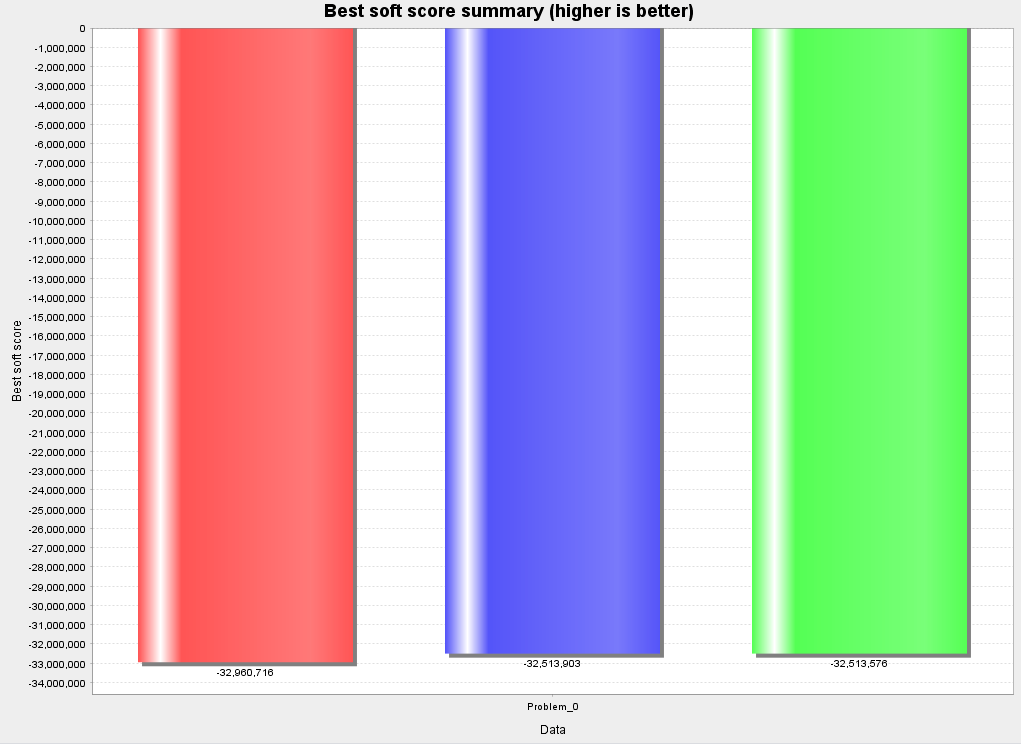
软约束结果对比

可以看到几种主要算法总体能得到的效果差异不大。从理论上来说，即使采用暴力搜索（Brute Force）的方式，只要时间够长，也总能得到一个不错的解。

而在实际的业务场景中，对于班表的计算速度是有很严苛的要求的。有时我们发现预测的业务量产生偏差，这时候就需要立刻重新生成当天之后的班表，并及时下发。对时间的要求是分钟级的，因此也要测试一下算法的运行速度。

几个重要算法的部分测试结果：

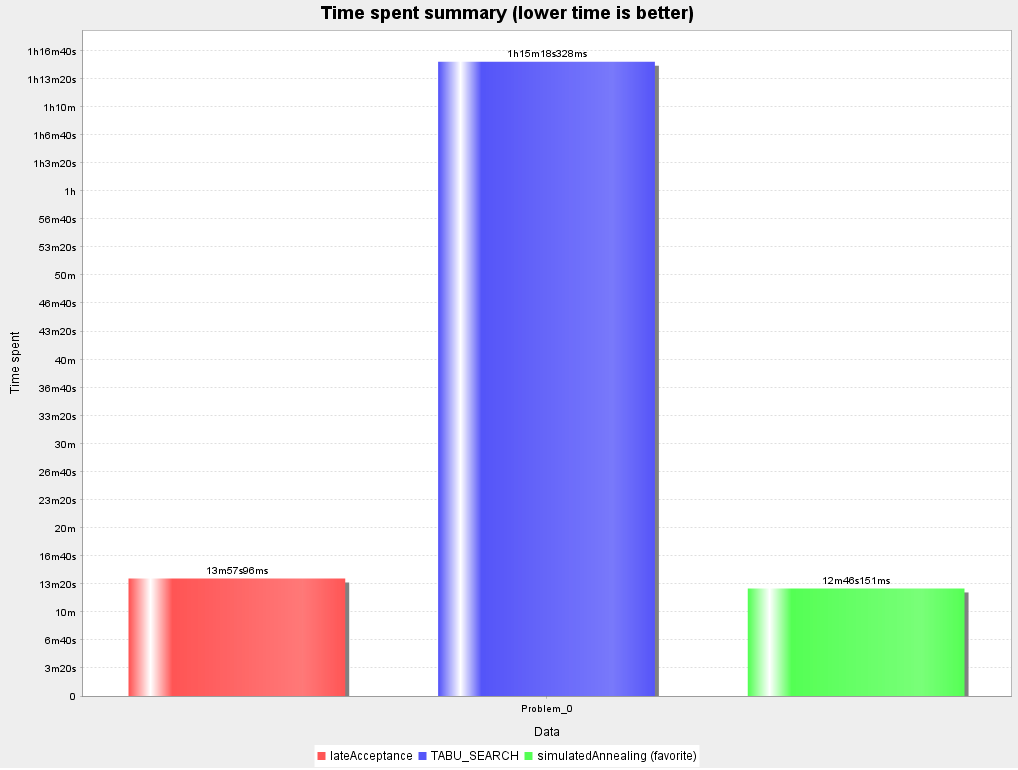
算法时间测试结果

而几个算法的提升速度，测试下来短期 Tabu Search 的结果提升较快，不过后续乏力，整体略逊于另外两个算法。

5.2 应用

这里的算法基准测试只是初步筛选一下可能有用的算法，整个计算流程中，从班次的确定，再到休息，加班，放休等的安排，实际是分多个层次的。从逻辑上讲，顺序应该是：

• 确定班次

• 确定加班放休安排

• 确定休息，吃饭等当天安排

• 确定周会安排

我们算法流程设计上也必须遵循一定的顺序，毕竟在班次没确定的情况下，我们也没办法安排当天的餐休。

因此流程上：

• 先安排了 First Fit，快速得到一个不太差的初始解。

• 接下来选择能够短时快速提升的 Tabu Search，仅仅针对班次，快速搜索找到一片高分区域。

• 最后利用 LAHC 或 Simulated Annealing 等算法针对全部变量搜索一个较优解。

5.3 性能优化     

在我们的业务场景中，问题规模很大，正常计算需要数小时甚至数天才能得到最终的结果，这一场景下是不可接受的。

一般的算法系统框架都是单机甚至单核的，这里首先要对算法系统进行多核支持，启发式算法的流程分为：

• 选择待选步骤

• 各步骤尝试

• 确定下一步（或者找不到下一步）。

对整个流程进行梳理后，我们判断整个算法性能消耗最多的地方是第二步，也就是各个步骤的尝试部分，在这一步加入多线程的支持，在选择了待选步骤后，对各个待选项进行多线程的并行尝试。

事实证明，这一步将性能提升 10 倍以上。

5.4 分布式多机并行

但在有些场景下依然不能满足目标性能的需求，无法在 30 分钟内得到班表。因此我们不得不利用分布式计算的思想，将问题进行切分，尝试在多机上进行并行计算，最后将结果汇总，在主机上进行汇总计算。

了解启发式算法的同学应该清楚，这样每台单机都获得的是问题的一个子集，缺点是无法全局考虑问题，最终结果和单机运算相比会略有下降。但是性能确实成倍的提升，在多工种的特殊场景中，我们通过这种思路，实现了复杂工种技能下的混合排班。并且最终效果也依然能够达到我们对拟合度的要求。在启发式搜索问题中，这是一种损失少量效果而大幅提升速度的有效技巧。

六、平台结构

在算法的基础上，我们搭建了一套智能排班中台作为项目目标，使用户可以轻松访问服务，得到灵活的班表。

整体架构示意图：

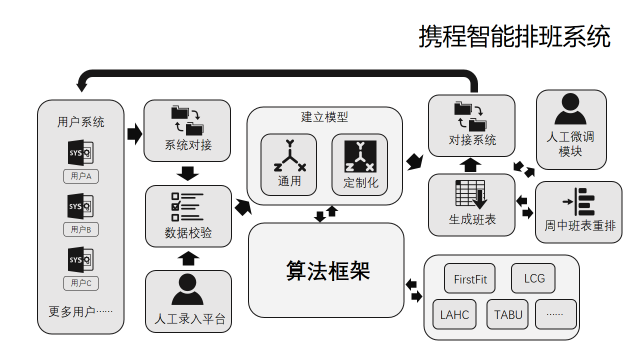
整个系统包含多个模块，互相协调保证携程各个部门的灵活调用。

总体调用流程如下：

1）各个 BU 通过系统对接排班系统，将数据做清洗和标准化

2）进行基本的数据校验，在实际环境中，各种各样隐藏的矛盾错误数据，都需要在这一步识别出来。

3）合并人工录入的部分数据，考虑到部分数据的时效性以及一些偶发需求，我们需要开放人工信息的录入平台，让用户可以录入部分数据

4）建立模型

5）算法求解得到优质解

6）生成班表

7）（可选）人工微调

8）生成班表，并对接回各个业务系统

七、结语    

随着越来越多的 BU 接入到智能化排班的系统中，算法平台发挥着更大的作用。在不断接触不同部门的过程中，我们也发现了模型建立中和算法设计中的各种问题。在我们长期的开发过程中，也走过不少弯路和死胡同，最终发现，需要全局的去看待一个业务问题，并提出解决方案，抓住真实痛点，才能最终落地。

作者简介 

博天，携程高级研发经理，关注大规模约束优化问题的建模和算法设计。

本文转载自：携程技术（ID：ctriptech）

原文链接：干货 | 10分钟给上万客服排好班，携程大规模客服排班算法实践