欢迎阅读新一期的内核杂谈。这是向量数据库的第四弹!这一期,咱们继续学习如何优化向量的存储和查询的技术,quantization 和 hierarchical navigable small worlds。这两个专有名词可能对很多同学来说都比较陌生,但希望经过这一期的学习,可以为大家 demystify 它们!
Quantization(量化)
前几期,咱们介绍了 tree-based approach 和 sharding-based approach,它们都是通过引入不同类型的数据结构来存储(indexing)和查询 vectors。Quantization 技术,是通过对原生的 vectors 进行压缩优化,从而达到节省整体的存储 vector 容量的目的(进一步,由于存储优化了,计算时使用的资源也得到了优化)。也因此,Quantization 技术和前几期介绍的技术是可以共用来达到更大的优化。我们依次介绍不同类型的 quantization 技术。
Scalar Quantization
Scalar Quantization 是最简单易懂的 quantization 技术,它通过将大空间的向量转换成相对小空间的向量来减少整体的存储空间。通常是将浮点数(比如 f32)向量量化成整数(比如 int8)向量(存储的优化比是 4X):也可以认为是将 2^32 映射到 2^8 的空间里。原先不同的浮点数可能在映射后就变成同一个值。因此,scalar quantization 是通过牺牲了计算精度来提升存储和查询效率。
下面,咱们结合代码来看如何实现 Scalar quantization。首先,我们随机生成一个 128 维的 1000 size 的向量组。
import numpy as npdataset = np.random.normal(size=(1000, 128))接下来,我们需要将浮点数转换到 int8 的空间里。推荐大家也可以思考一下算法。一种可行的算法是:针对每一个 dimension,遍历所有的数字得到 min 和 max 值,然后将 min 值映射到 0(int8 的 min 值),max 值映射到 255(int8 的 max 值),然后,通过(max - min)/255 计算出 step 值。相当于把 min 到 max 划分成了 255 个桶,然后对原先的数字进行桶排序,将原先向量中的浮点数替换成桶的 ID 数,就做到了 f32 到 int8 的映射。在映射的过程中,也尽量保证了向量之间的差异。代码实现也非常直观:得到每个维度的 min,max 值:
ranges = np.vstack((np.min(dataset, axis=0), np.max(dataset, axis=0)))计算出 step 值,并将每一个 vector 映射到 int8 的桶里:
starts = ranges[0,:]steps = (ranges[1,:] - ranges[0,:]) / 255dataset_quantized = np.uint8((dataset - starts) / steps)打印 dataset_quantized,大致会得到下面这样的输出:

下面的代码将 scalar quantization 封装起来使用:
import numpy as npclass ScalarQuantizer: def __init__(self): self._dataset = None def create(self): """Calculates and stores SQ parameters based on the input dataset.""" self._dtype = dataset.dtype # original dtype self._starts = np.min(dataset, axis=1) self._steps = (np.max(dataset, axis=1) - self._starts) / 255 # the internal dataset uses `uint8_t` quantization self._dataset = np.uint8((dataset - self._starts) / self._steps) def quantize(self, vector): """Quantizes the input vector based on SQ parameters""" return np.uint8((vector - self._starts) / self._steps) def restore(self, vector): """Restores the original vector using SQ parameters.""" return (vector * self._steps) + self._starts @property def dataset(self): if self._dataset: return self._dataset raise ValueError("Call ScalarQuantizer.create() first")dataset = np.random.normal(size=(1000, 128))quantizer = ScalarQuantizer(dataset)(scalar quantization code example: reference from: https://zilliz.com/blog/scalar-quantization-and-product-quantization)
Vector Quantization
Vector quantization 是另一类简单的 quantization 技术。区别于 scalar quantization 是分别从每一个维度进行压缩,vector quantization 是通过将原始向量当做一个整体去看待,将一个向量映射到指定的参考向量里(通常,指定的参考向量被称为码本,vector codebook)。虽然,每一个向量并没有从存储 size 上减小,但你可以认为所有要存储的向量都在这个码本里,只要码本的 size 足够小,带来的存储上的收益就非常大。
如何构建具有代表性的码本呢?又可以搬出我们介绍过的 k-means 算法了。k-means 算法通过将空间上相似的向量聚类到一起,并通过 centroid 质点来代表这个聚类。因此,vector quantization 可以通过将所有的向量都映射到相应的聚类的质点向量来提升存储效率。
Product Quantization
Vector quantization 是将向量空间里的所有 dimension 都考虑进来,然后将每个向量映射到码本的参考向量里。实际情况中,最常见的 quantization 技术是 product quantization,它和 vector quantization 的区别在于,将所有的 dimension 划分成 subspace,然后每个 subspace 独立去做 vector quantization(通过 k-means 找到代表这段 subspace 的质点)。下面是 product quantization 的具体算法描述:
1)给定一个包含 N 个总向量的数据集(设定为 d dimension),我们首先将每个向量划分为 M 个子向量(也称为子空间),每个子空间的 dimension 为 d/M。这些子向量的长度不必完全相同,但实际情况下,推荐使用相同的长度(方便代码实现)。
2)对数据集中所有子向量使用 k-均值(或其他聚类算法)。这会为每个子空间给出一组 K 个质心,每个质心都将被分配其唯一的 ID。
3)在计算出所有质心后,我们将用其最近质心的 ID 替换原始数据集中的所有子向量。
4)给定一个新的 d dimension 的向量,分成 M 个子向量,分别对应每个子向量找到对应的质心,然后用质心 ID 组合起来。
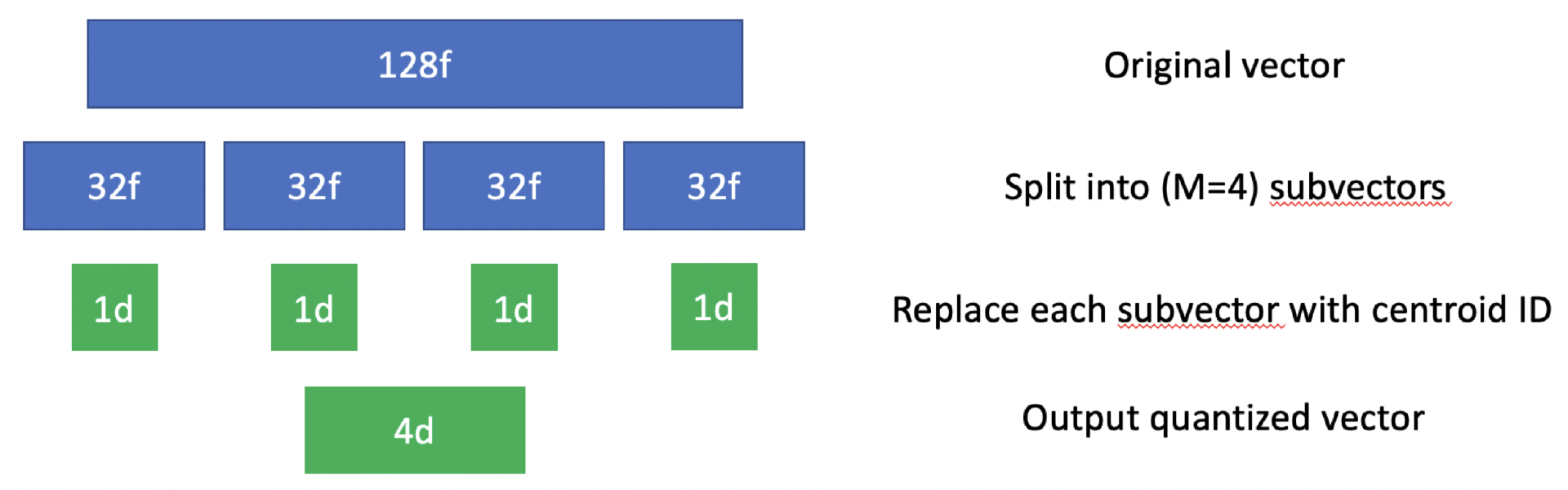
(product quantization 示例)
Production quantizer 的实现代码如下(下面的代码将原生的 vector 划分成 16 个 subspace,然后每个 subspace 用 k=256 个 cluster 来表达):
import numpy as npfrom scipy.cluster.vq import kmeans2class ProductQuantizer: def __init__(self, M=16, K=256): self.M = 16 self.K = 256 self._dataset = None def create(self, dataset): """Fits PQ model based on the input dataset.""" sublen = dataset.shape[1] // self.M self._centroids = np.empty((self.M, self.K, sublen), dtype=np.float64) self._dataset = np.empty((dataset.shape[0], self.M), dtype=np.uint8) for m in range(self.M): subspace = dataset[:,m*sublen:(m+1)*sublen] (centroids, assignments) = kmeans2(subspace, self.K, iter=32) self._centroids[m,:,:] = centroids self._dataset[:,m] = np.uint8(assignments) def quantize(self, vector): """Quantizes the input vector based on PQ parameters""" quantized = np.empty((self.M,), dtype=np.uint8) for m in range(self.M): centroids = self._centroids[m,:,:] distances = np.linalg.norm(vector - centroids, axis=1) quantized[m] = np.argmin(distances) return quantized def restore(self, vector): """Restores the original vector using PQ parameters.""" return np.hstack([self._centroids[m,vector[m],:] for m in range(M)]) @property def dataset(self): if self._dataset: return self._dataset raise ValueError("Call ProductQuantizer.create() first")dataset = np.random.normal(size=(1000, 128))quantizer = ProductQuantizer()quantizer.create(dataset)# quantize a new vectortest_vector = np.random.normal(size=(1, 128))quantized = quantizer.quantize(test_vector)# restore to original dimension vector (using centroids)quantizer.restore(quantized)为什么说 product quantization 比其他两类方法在实际应用中效果更好呢?找到的理由是,划分成多个 subspace,比不划分(vector quantization)或者只考虑单个 dimension 的方法,(scalar quantization)能够在高维的向量空间中,更有效地捕捉到不同维度的相似度(correlation),因此在存储空间优化和准确性上有更好的平衡。感觉,这个有点玄学。不过介绍也说,通常情况下表现更好,但最好的方法还是通过不同的实验去比较不同方法的优劣。
Hierarchical Navigable Small Worlds (HNSW)
接下来要学习的是目前最广泛使用的算法,Hierarchical Navigable Small Worlds (由于我并没有找到对应的中文名称,下文就用 HNSW 来表示)。HNSW 在查询速度和准确度上有非常好的平衡,也因此成为最受欢迎的 vector search 的算法。要学习 HNSW,需要先熟悉两个概念,skip-list(跳表)和 Navigable Small Worlds (NSW)。
Skip-List(跳表)
介绍网上已经有大量的优质的介绍 skip-list 的文章了,咱们稍稍简单介绍一下。要介绍跳表,先得从众所周知的链表(Linked-List)说起,一种每个元素都维护下一个元素(或者同时维护上一个元素)的指针的著名数据结构(数据结构和算法 101)。尽管链表非常适合实现 last-in first-out(LIFO)和 first-in first-out(FIFO),如堆栈和队列,但在随机访问的时间复杂度表现较差,是 O(n)。跳表旨在通过引入额外的中间层来优化这个复杂度,从而实现 O(log n)的随机访问时间复杂度,同时增加额外的内存(与普通链表的 O(n)相对,空间复杂度为 O(n log n)),以及插入和删除的运行时开销。跳表是一个多层链表,上层维护“长”连接。当我们向下层移动时,连接变得越来越短,最底层是包含所有元素的“原始”链表。在插入元素时,可以试用一个随机函数(roll the dice)来决定是否要插入一个中间层。跳表通常被拿来和平衡二叉树(比如 AVL-tree 或者 Black-red-tree)相比,因为它们的访问复杂度类似。跳表的优势在于实现相对容易,且在更频繁的更新用例(插入,删除)下表现相对更好。下图给出了一个跳表的示例:
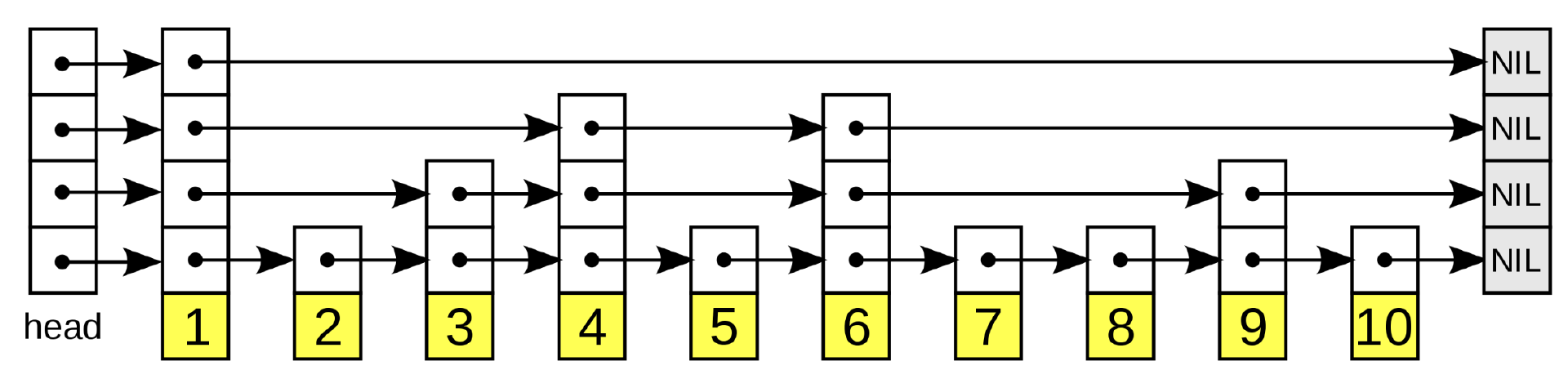
(跳表示例)
跳表的查询从最高层开始,在跳跃列表中到达元素 i。一旦我们找到一个与列表中大于 i 的元素对应的节点,我们就回退到前一个节点并移动到下面的层。这一过程一直持续到我们找到我们正在寻找的元素为止。注意,跳跃列表仅适用于排序列表,因为我们需要一种直接比较两个对象大小的方法。
跳表的中间层插入是基于概率的。对于任何新元素,首先需要弄清楚元素首次出现的层。最上层的概率最低,随着在层中向下移动,概率逐渐增加。一般规则是,某一层中的任何元素都会以某个预定的概率 p 出现在它上面的层中。因此,如果元素首次出现在某个层 l 中,它还将被添加到 l-1、l-2 等层中。
Navigable Small World 介绍
介绍了跳表后,我们来学习一下 Navigable Small Worlds(下面简称 NSW)。首先想象一个网络,网络上有许多节点,这些节点有些相互联通。每个节点会和联通的节点有短距离、中距离或者长距离的连接。
在执行搜索时,我们将从某个预先设定的的入口点开始搜索。从那里,我们通过比较搜索点和这个点以及其联通的点的距离,并跳转到距离搜索点节点最近的节点。这个过程重复,直到我们找到最近的邻居。这种搜索称为贪心搜索。这个算法适用于数百或数千个节点的小型 NSW,但对于更大的 NSW 则效率比较低。一个优化方法是通过增加每个节点的短距离、中距离和长距离连接的节点的数量,但这会增加网络的整体复杂性,并导致搜索时间变长。
将向量数据集中的所有向量想象成 NSW 中的点,长距离连接的点表示彼此不相似的两个向量,短距离连接的点则相反,表示两个近似的向量。通过这种方式,将整个数据集向量构建成 NSW,我们可以通过贪婪算法遍历 NSW,朝着越来越接近搜索向量的顶点方向移动,完成近邻搜索。
HNSW 的查询和构建
在实际应用中,向量数据集包含着成千上亿个向量,简单的 NSW 的搜索效率太低了。于是,诞生了结合跳表和 NSW 的 HNSW:与跳表一样,HNSW 是一个多层级的数据结构,每层不是链表,而是由 NSW 构成(如下图所示)。
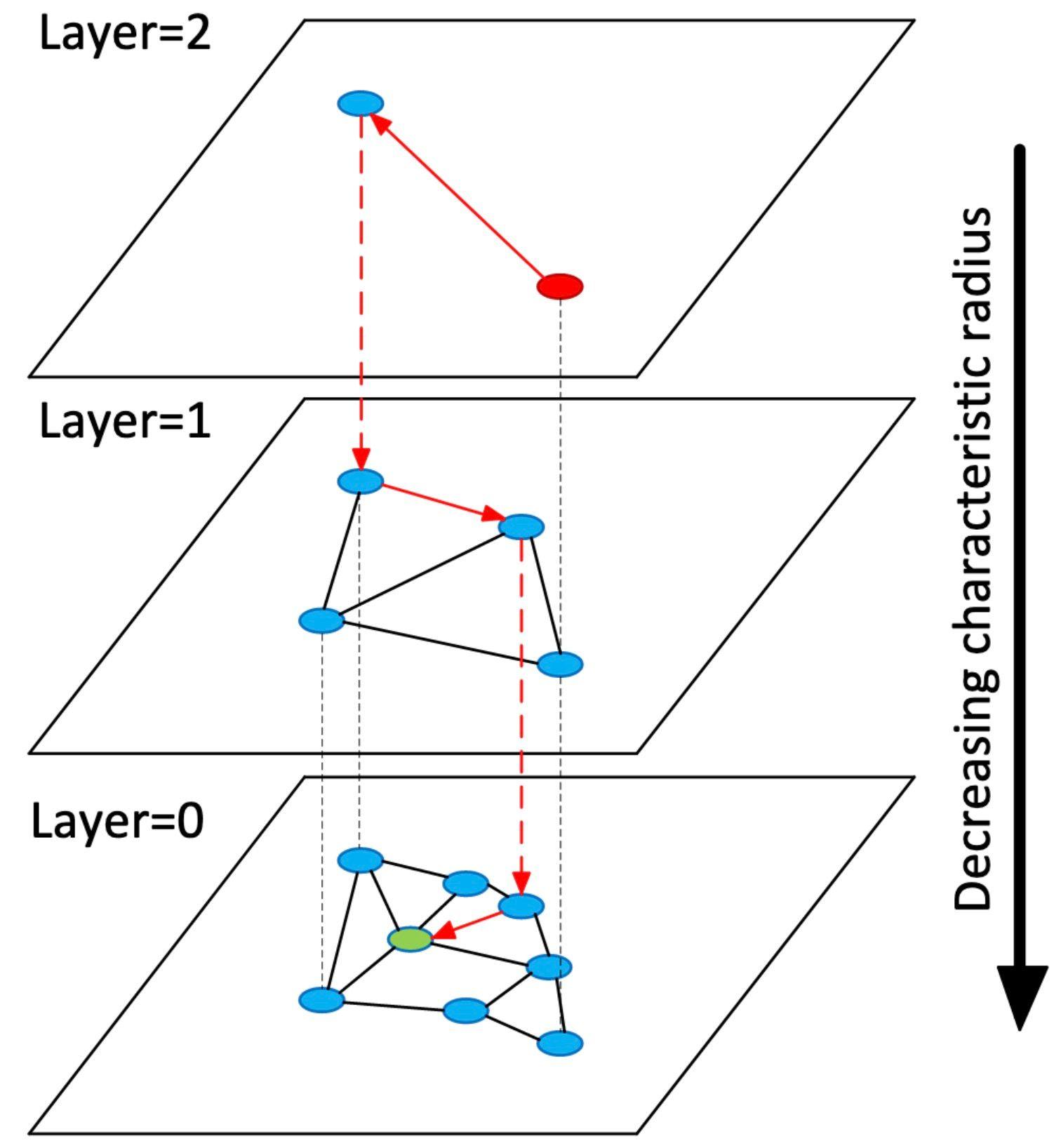
(HNSW 示例)
HNSW 图的最上层有很少的节点,且节点间的距离都很长。而最底层则包括所有节点和最短的链接。搜索过程如下:给定一个查询向量,我们先进入最上层的一个预定义的搜索起点,并通过贪婪算法朝着与我们的查询向量最近的邻居方向前进。一旦到达最近的节点,我们就在第二层重复此过程。这个过程一直持续到最底层,直到我们找到最近的邻居节点,搜索结束。
HNSW 的另一个优势,区别于我们已经学习过的其他向量存储方式,就是更高效地支持插入新的向量。插入操作和跳表的插入操作类似。对于某个向量 v,我们先通过搜索算法,找到这个向量在最底层的位置:首先遍历图的第一层,找到它的最近邻居,然后移到其下方的层次;然后,再次遍历图,以在第二层找到它的最近邻居;这个过程一直持续,直到在最底层的图中找到最近的邻居。
第二步,需要确定向量 v 和哪些现有节点建立连接(顶点之间的连接)。通常会设定一个预定义的参数 M,它决定了我们可以添加的双向链接的最大数量。这些链接通常设置为 v 的最近邻居。与跳表一样,查询向量在上层出现的概率呈指数递减,可以试用一个随机函数来判断是否要创建上层的节点。
总结
这一期,我们一起学习了 quantization 和 hierarchical navigable small worlds。Quantization 技术能够压缩向量存储的空间,且可以和其他存储技术一起使用。 HNSW 是目前最被广泛使用的向量存储和检索技术,通过跳表方式构建的多维 NSW 在构造和搜索向量数据集都有不错的表现。至此,咱们把构建向量数据库所用到的常用技术和算法都学习了。 下一期,我们会从构建一个向量数据库的角度出发,从整体看如何将这些单点能力串联起来。感谢阅读!





