使用并行计算大幅提升递归算法效率

前言：

无论什么样的并行计算方式，其终极目的都是为了有效利用多机多核的计算能力，并能灵活满足各种需求。相对于传统基于单机编写的运行程序，如果使用该方式改写为多机并行程序，能够充分利用多机多核 cpu 的资源，使得运行效率得到大幅度提升，那么这是一个好的靠谱的并行计算方式，反之，又难使用又难直接看出并行计算优势，还要耗费大量学习成本，那就不是一个好的方式。

由于并行计算在互联网应用的业务场景都比较复杂，如海量数据商品搜索、广告点击算法、用户行为挖掘，关联推荐模型等等，如果以真实场景举例，初学者很容易被业务本身的复杂度绕晕了头。因此，我们需要一个通俗易懂的例子来直接看到并行计算的优势。

数字排列组合是个经典的算法问题，它很通俗易懂，适合不懂业务的人学习，我们通过它来发现和运用并行计算的优势，可以得到一个很直观的体会，并留下深刻的印象。问题如下：

请写一个程序，输入 M，然后打印出 M 个数字的所有排列组合（每个数字为 1，2，3，4 中的一个）。比如：M=3，输出：

 
1，1，1
1，1，2
……
4，4，4

共 64 个

注意：这里是使用计算机遍历出所有排列组合，而不是求总数，如果只求总数，可以直接利用数学公式进行计算了。

一、单机解决方案：

通常，我们在一台电脑上写这样的排列组合算法，一般用递归或者迭代来做，我们先分别看看这两种方案。

1) 单机递归

可以将 n（1<=n<=4）看做深度，输入的 m 看做广度，得到以下递归函数（完整代码见附件 CombTest.java）

 
public void comb(String str){
   for(int i=1;i<n+1;i++){
       if(str.length()==m-1){
           System.out.println(str+i);
           total++;
       } else {
           comb(str+i);
       }
   }
}

但是当 m 数字很大时，会超出单台机器的计算局限导致缓慢，太大数字的排列组合在一台计算机上几乎很难运行出，不光是排列组合问题，其他类似遍历求解的递归或回溯等算法也都存在这个问题，如何突破单机计算性能的问题一直困扰着我们。

2) 单机迭代

我们观察到，求的 m 个数字的排列组合，实际上都可以在 m-1 的结果基础上得到。

比如 m=1，得到排列为 1,2,3,4，记录该结果为 r(1)

m=2, 可以由 (1,2,3,4)* r(1) = 11,12,13,14,21,22,…,43,44 得到, 记录该结果为 r(2)

由此，r(m) =(1,2,3,4)*r(m-1)

如果我们从 1 开始计算，每轮结果保存到一个中间变量中，反复迭代这个中间变量，直到算出 m 的结果为止，这样看上去也可行，仿佛还更简单。

但是如果我们估计一下这个中间变量的大小，估计会吓一跳，因为当 m=14 的时候，结果已经上亿了，一亿个数字，每个数字有 14 位长，并且为了得到 m=15 的结果，我们需要将 m=14 的结果存储在内存变量中用于迭代计算，无论以什么格式存，几乎都会遭遇到单台机器的内存局限，如果排列组合数字继续增大下去，结果便会内存溢出了。

二、分布式并行计算解决方案：

我们看看如何利用多台计算机来解决该问题，同样以递归和迭代的方式进行分析。

1) 多机递归

做分布式并行计算的核心是需要改变传统的编程设计观念，将算法重新设计按多机进行拆分和合并，有效利用多机并行计算优势去完成结果。

我们观察到，将一个 n 深度 m 广度的递归结果记录为 r(n,m)，那么它可以由 (1,2,…n)*r(n,m-1) 得到：

r(n,m)=1_r(n,m-1)+2_r(n,m-1)+…+n*r(n,m-1)

假设我们有 n 台计算机，每台计算机的编号依次为 1 到 n，那么每台计算机实际上只要计算 r(n,m-1) 的结果就够了，这里实际上将递归降了一级， 并且让多机并行计算。

如果我们有更多的计算机，假设有 n*n 台计算机，那么：

r(n,m)=11_r(n,m-2)+12_r(n,m-2)+…+nn*r(n,m-2)

拆分到 n*n 台计算机上就将递归降了两级了

可以推断，只要我们的机器足够多，能够线性扩充下去，我们的递归复杂度会逐渐降级，并且并行计算的能力会逐渐增强。

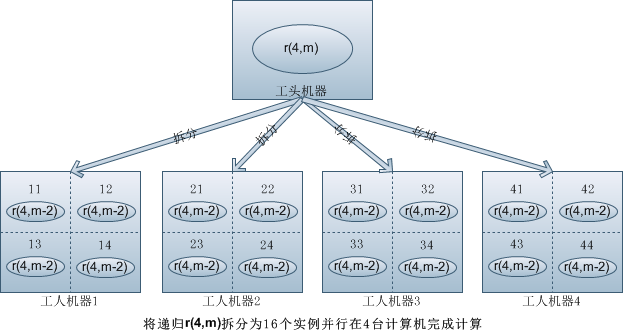
这里是进行拆分设计的分析是假设每台计算机只跑 1 个实例，实际上每台计算机可以跑多个实例（如上图），我们下面的例子可以看到，这种并行计算的方式相对传统单机递归有大幅度的效率提升。

这里使用 fourinone 框架设计分布式并行计算，第一次使用可以参考分布式计算上手demo 指南, 开发包下载地址： http://www.skycn.com/soft/68321.html

ParkServerDemo：负责工人注册和分布式协调

CombCtor：是一个包工头实现，它负责接收用户输入的 m，并将 m 保存到变量 comb，和线上工人总数 wknum 一起传给各个工人，下达计算命令，并在计算完成后累加每个工人的结果数量得到一个结果总数。

CombWorker：是一个工人实现，它接收到工头发的 comb 和 wknum 参数用于递归条件，并且通过获取自己在集群的位置 index，做为递归初始条件用于降级，它找到一个排列组合会直接在本机输出，但是计数保存到 total，然后将本机的 total 发给包工头统计总体数量。

运行步骤：

为了方便演示, 我们在一台计算机上运行:

1. 启动 ParkServerDemo：它的 IP 端口已经在配置文件的 PARK 部分的 SERVERS 指定。
2. 启动 4 个 CombWorker 实例：传入 2 个参数，依次是 ip 或者域名、端口（如果在同一台机器可以 ip 相同，但是端口不同），这里启动 4 个工人是由于 1<=n<=4，每个工人实例刚好可以通过集群位置 index 进行任务拆分。
3. 运行 CombCtor 查看计算时间和结果

下面是在一台普通 4cpu 双核 2.4Ghz 内存 4g 开发机上和单机递归 CombTest 的测试对比

M=14 M=15 M=16 CPU 利用率 单机递归计算 10 秒 41 秒 169 秒 29% 单机并行计算 6 秒 26 秒 112 秒 99% 多机并行计算 按机器数量成倍提升效率 99%通过测试结果我们可以看到：

1. 可以推断，由于单机的性能限制，无法完成 m 值很大的计算。
2. 同是单机环境下，并行计算相对于传统递归提升了将近 1.6 倍的效率，随着 m 的值越大，节省的时间越多。
3. 单机递归的 CPU 利用率不高，平均 20-30%，在多核时代没有充分利用机器资源，造成 cpu 闲置浪费，而并行计算则能打满 cpu，充分利用机器资源。
4. 如果是多机分布式并行计算，在 4 台机器上，采用 4*4 的 16 个实例完成计算，效率还会成倍提升，而且机器数量越多，计算越快。
5. 单机递归实现和运行简单，使用 c 或者 java 写个 main 函数完成即可，而分布式并行程序，则需要利用并行框架，以包工头 + 多个工人的全新并行计算思想去完成。

2) 多机迭代

我们最后看看如何构思多机分布式迭代方式实现。

思路一：

根据单机迭代的特点，我们可以将 n 台计算机编号为 1 到 n

第一轮统计各工人发送编号给工头，工头合并得到第一轮结果{1,2,3,…,n}

第二轮，工头将第一轮结果发给各工人做为计算输入条件，各工人根据自己编号累加，返回结果给工头合并，得到第二轮结果：{11,12,13,1n,…,n1,n2,n3,nn}

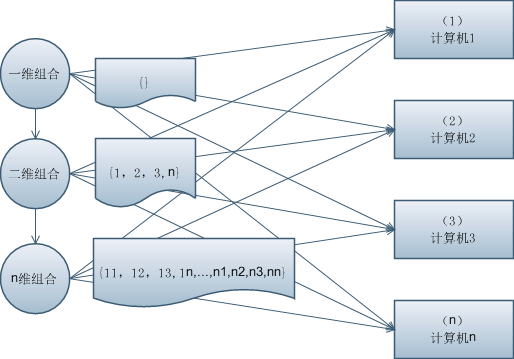
这样迭代下去，直到 m 轮结束，如上图所示。

但很快就会发现，工头合并每轮结果是个很大的瓶颈，很容易内存不够导致计算崩溃。

思路二：

如果对思路一改进，各工人不发中间结果给工头合并，而采取工人之间互相合并方式，将中间结果按编号分类，通过 receive 方式（工人互相合并及 receive 使用可参见 sayhello demo ），将属于其他工人编号的数据发给对方。这样一定程度避免了工头成为瓶颈，但是经过实践发现，随着迭代变大，中间结果数据越来越大，工人合并耗用网络也越来越大，如果中间结果保存在各工人内存中，随着 m 变的更大，仍然存在内存溢出危险。

思路三：

继续改进思路二，将中间结果变量不保存内存中，而每次写入文件（详见 Fourinone2.0 对分布式文件的简化操作），这样能避免内存问题，但是增加了大量的文件 io 消耗。虽然能运行出结果，但是并不高效。

总结：

或许分布式迭代在这里并不是最好的做法，上面的多机递归更合适。由于迭代计算的特点，需要将中间结果进行保存，做为下一轮计算的条件，如果为了利用多机并行计算优势，又需要反复合并产生中间结果，所以导致对内存、带宽、文件 io 的耗用很大，处理不当容易造成性能低下。

我们早已经进入多 cpu 多核时代，但是我们的传统程序设计和算法还停留在过去单机应用，因此合理利用并行计算的优势来改进传统软件设计思想，能为我们带来更大效率的提升。

下载完整代码点击这里