神经网络是机器学习的巅峰:它们可以通过使用极其复杂的函数匹配同样复杂的结构来建模。神经网络充满了非线性和信息传播流,而数据科学家的心态往往是“我们能很好地利用神经网络,但是也牺牲掉了一些可解释性。”诚然,算法的黑盒性质已为大多数人所接受,但不应该如此。
对算法应用来说,了解算法如何做出决策至关重要。在世界各地的组织中,神经网络被用来决定某人是否应该获批贷款,某人是否适合某项工作,甚至某人是否犯罪:用一种“在训练集上表现得很好”的态度,让无法解释的算法去解决这些重要的问题,不仅是危险的,而且也是不道德的。
每一个深度学习工程师都应该学习如何解释神经网络,可惜大多人并没有学会。 如果你能解释这个强大的建模器,那么在数据中反映的严重问题转变成更大的问题之前就能加以阻止,并且能获得人类可以理解的知识,例如关于肺癌症状的知识,这些知识对那些无法获得先进技术的应用和地点是非常有价值的。
对神经网络的解释将人的成分带入了这样一个人工结构中。
本文将介绍解释神经网络过程的三种方法以及评估解释质量的一种方法。
激活最大化
激活最大化(Activation Maximization)是一种可视化神经网络以使某些神经元的激活最大化的方法。在正常的训练过程中,人们通过迭代调整网络的权重和偏差,这样在数据集中的训练样本中,神经网络的误差或损失就会最小化。另一方面,激活最大化可以解决这一问题:在训练分类器之后,我们希望通过迭代寻找数据中模型认为属于某个类的部分。
举例来说,考虑一种识别 0 到 9 手写数字的神经网络的可视化(MNIST 数据集):我们想要知道,神经网络认为图像的哪些部分对于它决定了是哪个数字很重要;也许是 8 的下半圆或 0 的圆圈。
神经网络的激活函数输出表示训练样本属于某个特定类别的置信度,所以激活最大化构造一幅图像,并检查神经网络正在寻找的每个框,从而生成最大的激活函数。通过梯度上升可以达到这个目的,它试图最大化输出神经元。激活最大化的想法就是寻找输入来返回最高置信度的输出。
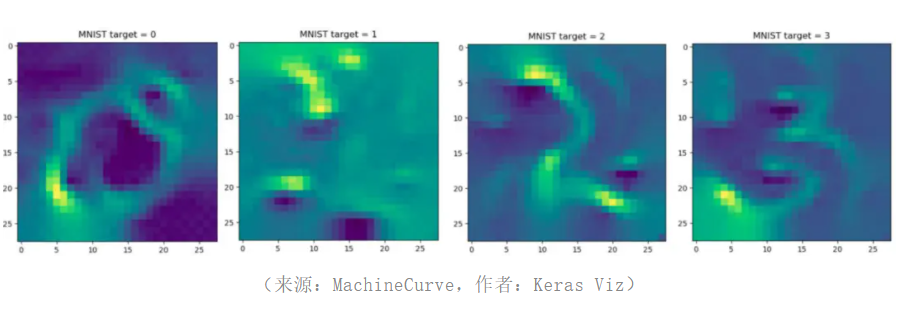
这一结果对于模型如何作出决策非常有启发意义,暗色区域表示“惩罚”,即该区域的高值将使模型不太确定输入的是哪个数字;而亮值表示“奖励”,即这些区域的高值将增加输出神经元的置信度。对于一维的非图像数据,激活最大化也可以用分布或其他分布表示的形式来可视化。
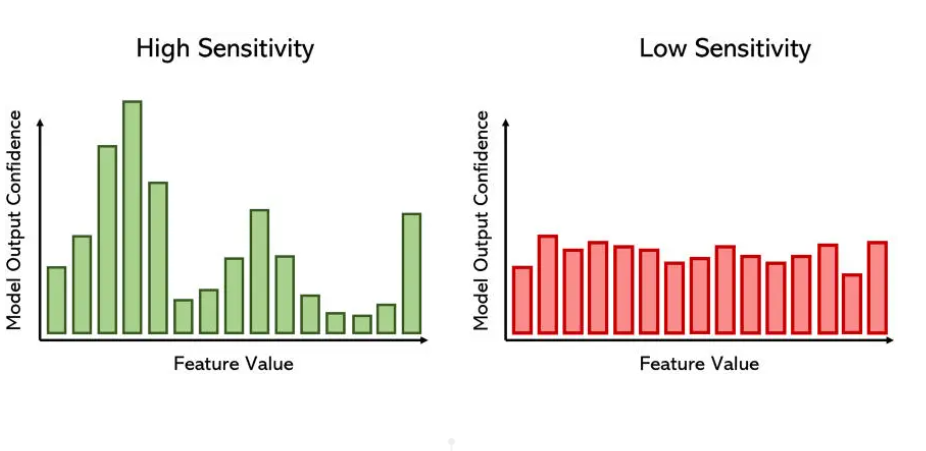
敏感度分析分析
敏感度分析(Sensitivity Analysis)是一种分析模型预测梯度的方法。若神经网络由一个函数 f(x) 来建模,其中,x 表示输入值的变量 (x[1],x[2],...,x[n]),那么敏感度定义为 f(x) 相对于 x[i] 的导数,其中,x[i] 是我们将要建模的特征。用外行人的话来说,敏感度分析衡量的是一个特征的变化对模型在某个目标的置信度产生相应的机会,或者模型对某个特征的敏感度。
这种技术不仅适用于深度神经网络的解释,而且在金融和医学领域也有强健的根基。
所以,问题是“是什么让这副图像与一艘船相仿?”而不是“是什么让这幅图片像一辆车?”,例如,激活最大化就可以回答这个问题。这可被视为一种度量特征重要性的方法,但更重要的是,它显示了改变特征值如何影响输出的置信度,而非告诉我们它是真的。
分层相关传播
前面讨论的方法仅利用神经网络模型的输入 / 输出流,因此可以应用于任何算法的决策,而相关传播(Relevance Propagation)被明确地设计用于深度神经网络的前馈图结构。
假设我们有一幅狗的图像,神经网络将它按狗来分类,但是我们不确定它是否正确地识别了狗,还是以狗的碗作为上下文线索。所以我们可以把图像分成两部分,分别通过神经网络进行处理:如果狗的某一部分被分类为狗,而狗的碗没有进行分类,那么我们就知道这个模型可以泛化到其他狗的图像上。

相反,如果这两幅图像都按狗进行分类,那么可以认为,关于模型在完整图像的两个部分上放置的权重的信息是很少的。提示 LRP:分层相关传播(Layerwise Relevance Propagation)。
分层相关传播的目标是为输入向量 d 的每个元素定义一种相关性度量,即 R[d],这样神经网络的输出就是 R 的值之和,重述一下,分层相关传播试图将神经网络所发现的复杂关系压缩成一个加法问题;在信息高度浓缩的情况下,每个输入元素(特征)的 R 值既可解释,又有价值。
为了进行这种分解,总相关性得分(相当于输出)在开始的时候集中在输出上。然后,本着反向传播的精神,相关性得分被分解并分布到各个节点上,经过神经网络的每一层,直到到达输入层。
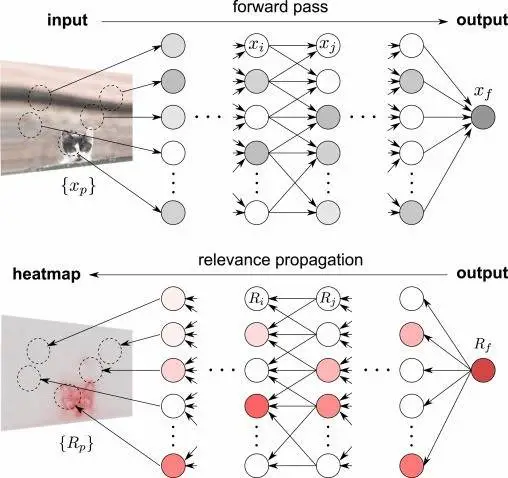
然后,输入层的相关性得分可以用热图或其他方式可视化;这些分数相加得到的结果是一样的,但能告诉我们很多信息,如输入节点的价值在其对结果的贡献中如何在神经网络架构中传播。
这类似于一个电路,有人在一个端点注入一定的电流,然后在其他端点计算接下来的电流,结果表明,电流较大的端点在整个系统的电流分布中具有更高的优先性和“重要性”。
这种独特的神经网络解释方法依赖于局部相关性守恒原理,该原理指出,由于网络中的信息可以保持不变,因此这种分解是可能的,这一点与适用于电流的基尔霍夫定律(基于能量守恒)相似。
解释连续性
对于解释神经网络的黑箱性质,有多种方法,每种方法都依靠自己的直觉和方法来解读结构,但量化解释的质量也很重要。如果不能给出准确的解释,再花哨的解释技术也毫无价值。
解释连续性(Explanation Continuity)植根于公平性度量,它指出,如果两个数据点几乎相等,那么对其预测的解释也应该几乎相等。
尽管这看起来是显而易见的,但解释连续性是一个比人们想象的更棘手的问题。例如,考虑对函数 max(x1,x2) 的解释,它只是简单地根据值的大小来设置坐标标签。解释方法有三种:敏感度分析、简单泰勒分解( Taylor decomposition,另一种寻找相关性得分的方法)和相关传播,这些方法对该函数都有不同的解释。
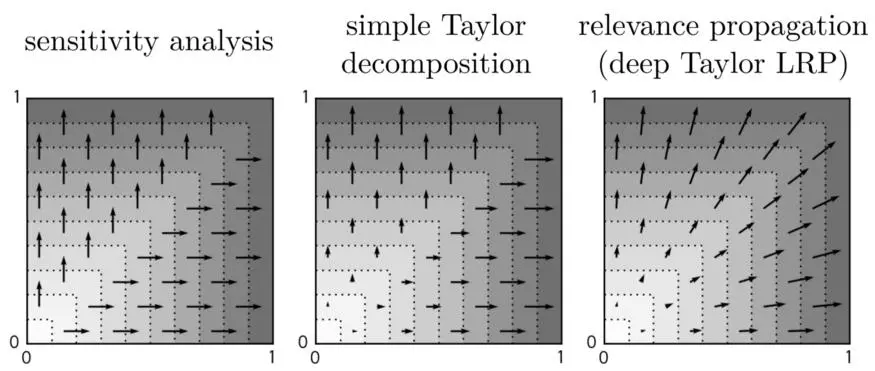
当 x1=x2 时,只有相关传播解释是连续的,并产生平滑的、基于环形的解释转变与敏感度和简单泰勒分解的结果相反,在 x1=x2 线上移动 0.001 点将产生完全不同的解释。
对像移动帧、旋转帧或增加噪音这样稍微改变的输入,如果解释需要有质量,那么对结果的解释不应有所改变。不然的话,解释技术可能不能正确地理解为什么输入会产生输出。
作者简介:
Andre Ye,机器学习和计算机科学爱好者。
原文链接:





