作者:张晟(OPPO 商业能力中心-商业平台部-召回开发团队)
编辑:李忠良
1.前言
随着 OPPO 商业化广告业务的发展,场景的不断接入,客户的不断增加,OPPO 广告播放引擎每天承载了百亿级别的流量以及百万级别的在线广告。而广告召回作为广告播放的第一个环节需要在有限资源内,尽可能快地从广告全集中筛选出价值最大化的广告子集。本文将介绍广告召回“快的秘密”-布尔检索(快速查找到符合条件的广告)
1.1 什么是广告召回系统?
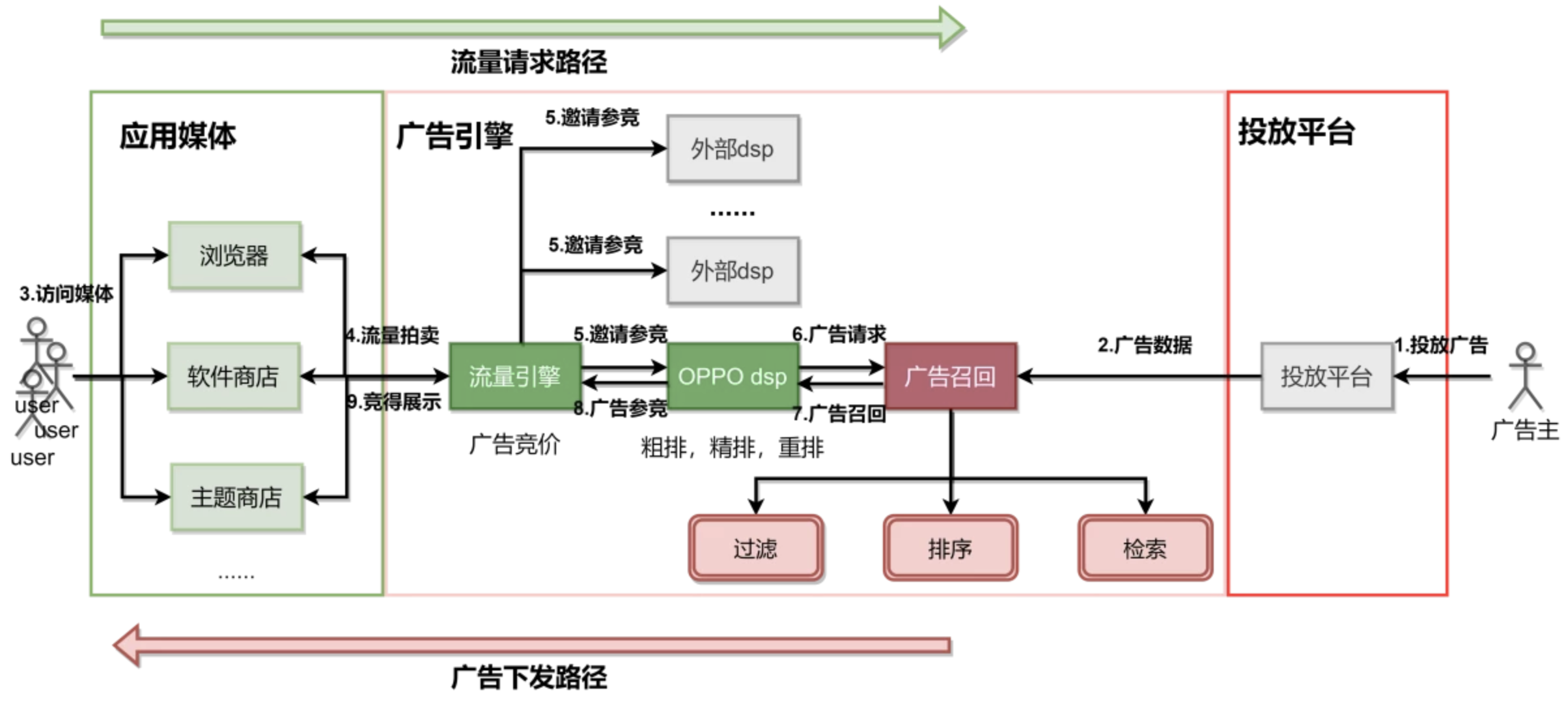
召回模块接收广告 DSP 发送来的广告请求,请求包含了用户信息和场景上下文信息。广告主设置的广告信息存在在线广告 DB 中,然后然后生成广告索引(Ad index),广告更新后实时或准实时地进行更新索引。
召回模块就是结合这两端选出初步的广告候选集,然后进入过滤模块(正排模块),过滤方法主要包括基于规则、黑白名单、广告主预算 pacing 过滤。最后通过一个简单的排序规则进行筛选截断,最终送入精排。
1.2 为什么需要广告索引?
在广告系统中倒排索引起着至关重要的作用,当请求过来时,需要根据定向信息从倒排索引中匹配合适的广告。这个过程要求快速精准。暴力搜索的方式固然可行,但虽然广告量级的增长,暴力搜索的耗时随广告量级线性增长,无法满足广告系统低时延的要求。
1.3 业界与开源
开源的一些方案可能难以支撑广告场景
Apache Lucene
全文检索、支持动态脚本;实现为一个 Library。
支持实时索引,但不支持层次结构。
Sphinx
全文检索;实现为一个完整的 Binary,二次开发难度大。
支持实时索引,但不支持层次结构。
广告业界
京东:主要是基于 op-index 的实现方式,基于主键分类的检索方式。
头条:主要是基于 k-index(我们后文介绍的方式)进行定制的广告索引结构。
2.倒排索引构建
从上面的介绍中我们可以了解到,召回系统中依赖倒排索引在竞价请求发生时, 快速从在线广告候选中取出满足条件的广告。今天这里介绍的是基于 Yahoo 和 Stanford 联合发布的论文:Boolean expression indexing 的实现。
2.1 广告数据“文档化”
首先,我们需要做的事将广告的数据进行标准化处理,例如广告主会对广告投放做一下定向要求(比如:性别,年龄,城市等)。将一个描述性语句进行文档化/甚至 id 化
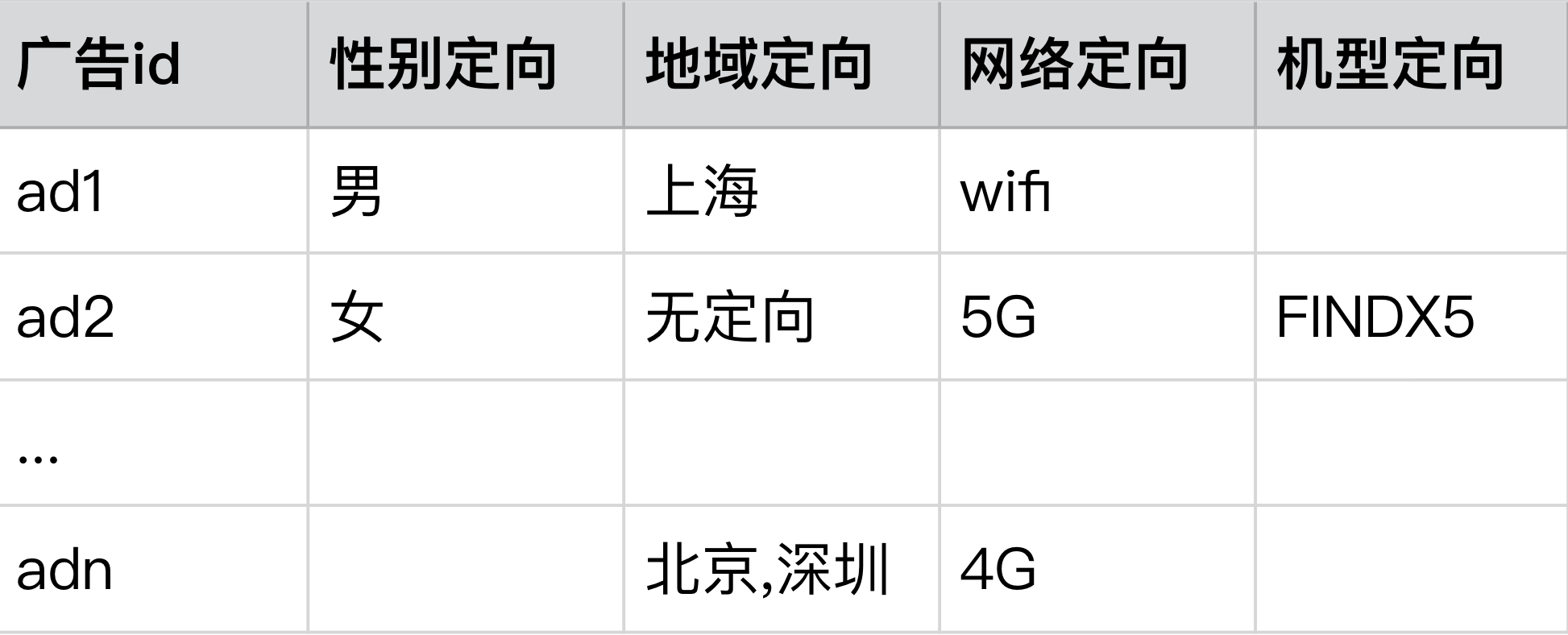
文档化(ID 化)
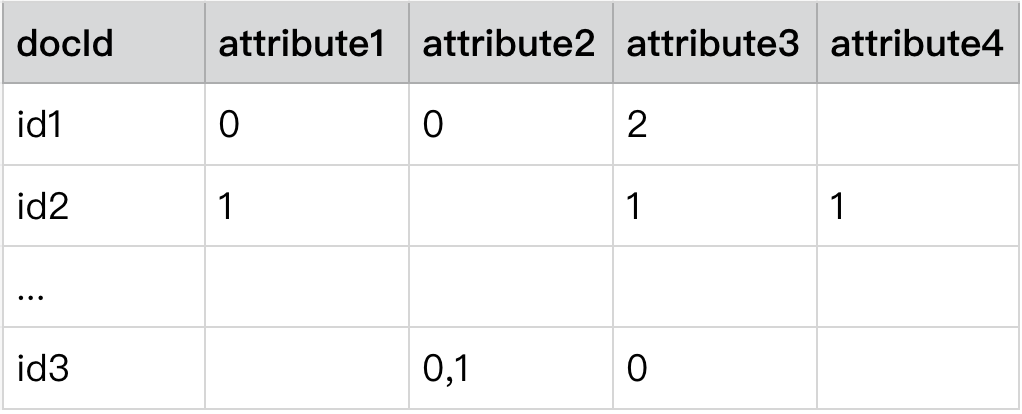
2.2 广告文档归一化为“析取范式”
通常用一个“析取范式”表示一个广告商的目标用户的需求。
析取范式(disjunctive normal form (DNF)
在布尔逻辑中,析取范式(DNF)是逻辑公式的标准化(或规范化),它是合取子句的析取。作为规范形式,它在自动定理证明中有用。一个逻辑公式被认为是 DNF 的,当且仅当它是一个或多个文字的一个或多个合取的析取。同合取范式(CNF)一样,在 DNF 中的命题算子是与、或和非。非算子只能用做文字的一部分,这意味着它只能领先于命题变量。例如,下列公式都是 DNF:

把公式转换成 DNF 要使用逻辑等价,比如双重否定除去、德·摩根定律和分配律。注意所有逻辑公式都可以转换成析取范式。但是,在某些情况下转换成 DNF 可能导致公式的指数性爆涨。例如,在 DNF 形式下,如下逻辑公式有 2n 个项:

简而言之,就是将广告主对用户筛选的诉求转化为,想要播放"我"投放的广告,用户需要满足:(条件 1 且 条件 2 且 条件 3) 或者 (条件 3 且 条件 4 且 条件 5)
《Boolean expression indexing》中将 (条件 1 且 条件 2 且 条件 3)这样一个合取子句,称为 Conjunction。将其中的一个条件表达式称为 Assignment。而 Assignment 则为一个三元组其他包含(attr:属性名/属性, predicate : 布尔原语(∈/∉), values:属性值)。
布尔逻辑
使用集合代数作为介绍布尔逻辑的一种方式。还使用文氏图来展示各种布尔逻辑陈述所描述的集合联系。
那么我们实际上需要做的就是将广告的定向信息,转化为一个布尔逻辑表达式:
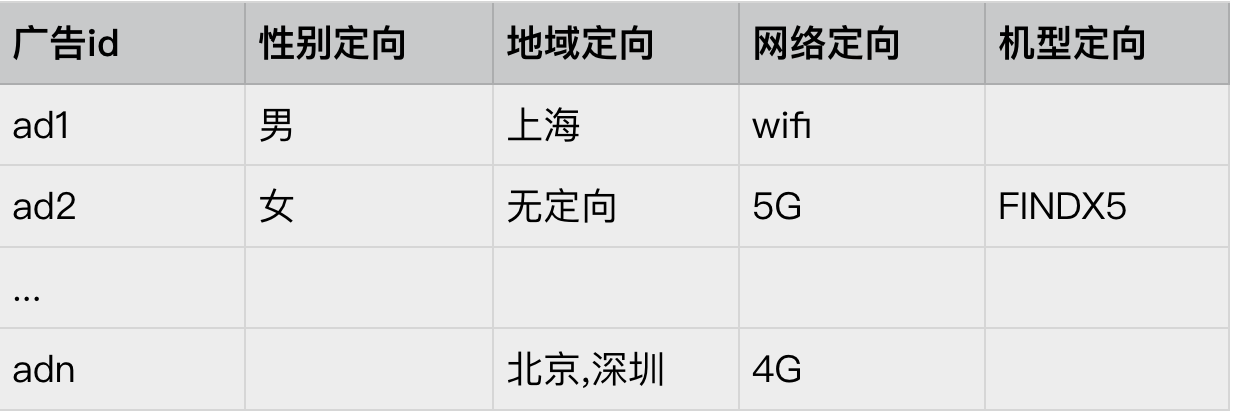
ad1->性别∈{男} & 地域 ∈{上海} & 网络 ∈{wifi}
其中
Conjunction1=性别∈{男} & 地域 ∈{上海} & 网络 ∈{wifi}
Assignment1 = 性别∈{男}
Assignment2 = 地域 ∈{上海}
Assignment3 = 网络 ∈{wifi}
...
最终所有的广告定向信息,均转化为如下的标准形式
ad1 Conjunction1 (Assignment1 & Assignment2)
ad2 Conjunction2 (Assignment4 & Assignment5)
ad3 Conjunction3 (Assignment2 & Assignment4)
.....
注意:通常,多数的广告平台(含 OPPO),对广告定向的支持仅停留在一组条件,即一个 Conjunction。我们这里举例的合取范式均使用单个 Conjunction。
2.3.布尔索引构建
2.1 和 2.2 的内容,主要介绍的是如何将广告的定向信息进行布尔逻辑的标准化流程。2.3 我们将介绍,这一系列的布尔逻辑表达式,如何组织成一个广告索引。
再介绍索引构建之前,我们再了解两个概念:
Conjunction id
Conjunction id:唯一表示一个 Conjunction,即 Conjunction 中的表达式相同,Conjunctionid 一定相同。例:
ad1: gender ∈ {F} ^ city ∈ {SZ}
ad2: gender ∈ {F} ^ city ∈ {SZ}
那么 ad1 和 ad2 Conjunction id 一定相同。
Conjunction size
Conjunction size:Conjunction 的所有 assignment 中,predicate 为∈的个数。例:
ad1:gender ∈ {M} ^ city ∉ {SZ} ^ network ∈ {WIFI} conj size = 2
ad2:city ∉ {SZ,SH} conj size = 0
通过一个例子来说明,假如我们的全量广告有如下 6 个。
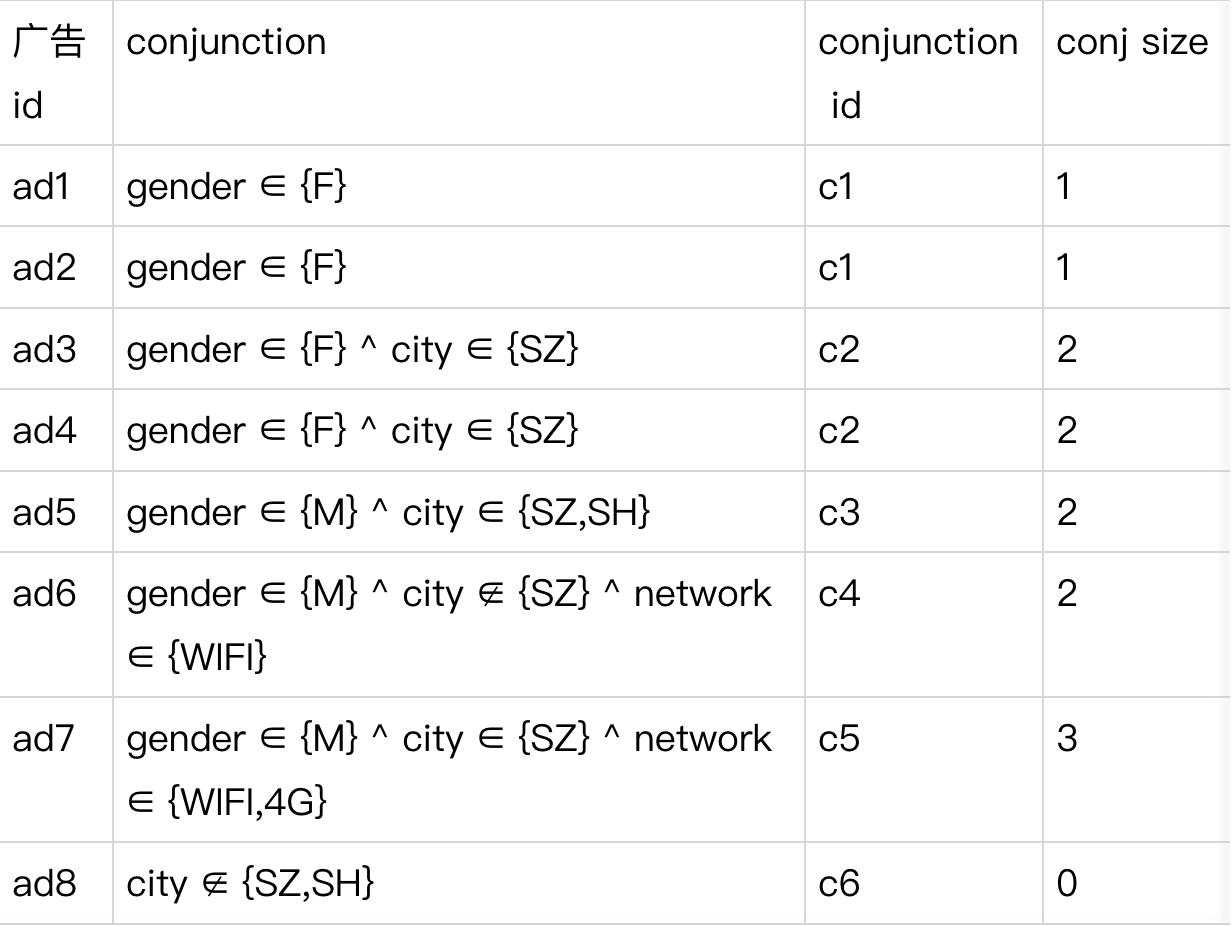
最终将构建成两层倒排索引:
第一级倒排索引:通过检索请求检索 Conjunction ID
第二级倒排索引:通过 Conjunction id 列表检索 adid 列表

2.3.1 第二级倒排
第二级倒排为 Conjunction id -> ad id 的倒排,构建的方式比较简单,即将所有相同 Conjunction id 的 ad 聚合起来生成一个 Conjunction id 到 ad 列表的哈希表即构建完成。

第二级倒排为第一级倒排检索出来的 Conjunction id 服务,当第一级检索返回了多个 Conjunction id,并根据 hash 表转换成所有满足条件的广告。
这里的 adlist 可以用 bitset 或者并行的方式进行优化,加快多个 list 的合并速度。
2.3.2 第一级倒排
有了第二级倒排,已经能够根据 Conjunction id 快速的找到对应的广告列表,那么如何
构建索引,高效地查找 Conjunction?
索引分层
首先, 来说先分层的概念。我们在构建布尔索引的时候,并不是把所有的 Conjunction 一起进行构建,而是会将其进行分类。我们的分类依据就是 2.3 节首先介绍的 Conjunction size。还是以如下这些广告为例:
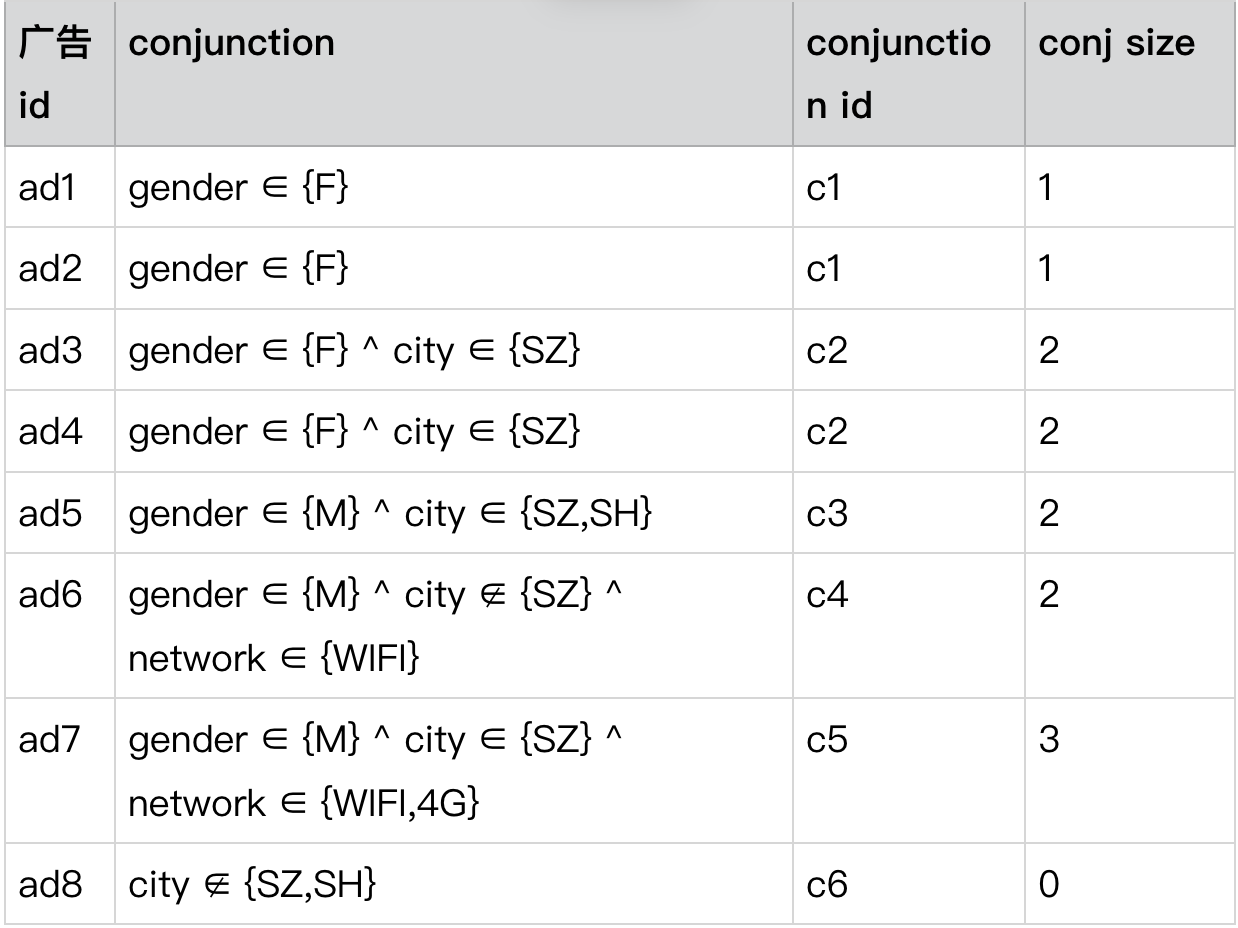
我们将其按 conj size 进行分层,分别构建 0,1,2,3 四层索引。分层的原因我们会在第三节 DNF 算法中进行介绍。分层将大大加快我们的匹配速度。
Level 0:

Level 1

Level 2:

Level 3:

每一层分别构建索引。
索引结构
在索引结构的介绍中,除了上文谈及的 Conjunction 和 assignment,还有 key,entry 和 postingList 三个概念这里一并进行介绍。
这里举个简单的例子,通常我们在新华字典中查“倒”字的时候,一般使用偏旁或者拼音中的声母来快速查找到对应的字。这里的偏旁或者字母属于这个字的一部分属性,而我们通过某些线索来找到对应的完整内容,这些线索叫 Key。此外通过偏旁或者声母能找到一系列同类型相似的字,这一系列有相同点的字就可以理解成 postingList,而其中的某个字就可以理解成最终我们要找寻的 Conjunction(entry)

在介绍第一级倒排之前,有几个概念需要了解。
Key
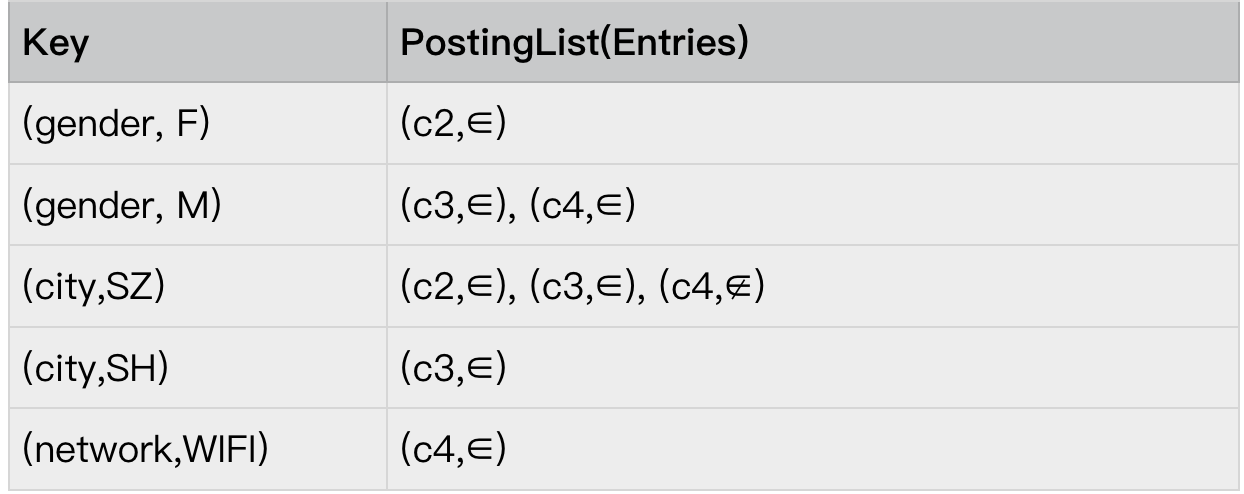
首先要了解的是 KEY 的概念,Conjunction 的 KEY 是(attribute,value)的二元组。还是以如下这个 Conjunction 为例:

我们知道在这个 Conjunction c4 中包含了 3 个 Assignment, 以 city ∈ {SZ,SH} 这个 Assignment 为例,它包含两个 KEY (city,SH) 和 (city,SZ)。
Entry
Entry 为(predicate,Conjunction Id)的二元组。且通常与该 Conjunction 对应的 KEY 成对出现,还是以 ad6 为例,

例如:c4: gender ∈ {M} ^ city ∉ {SZ} ^ network ∈ {WIFI}

PostingList
Entry 的列表则是 PostingList,不过唯一需要注意的是,PostingList 是一个有序的列表,它是按 Conjunction id 的大小排序,当 Conjunction id 相同时,则按 predicate 排序,∉ 的 entry 将排在∈的前面。

具体示例
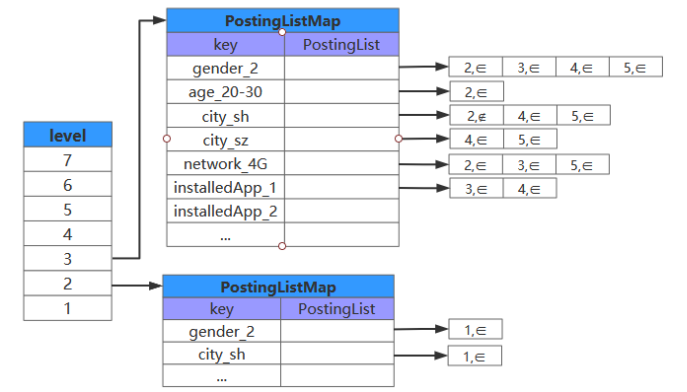
当我们了解索引的分层依据,以及层内,索引的具体结构后。我们将如下图中 Level2 的广告进行倒排索引构建。
Level2 广告

Level2 倒排
整体结构大致如下
布尔检索
当有了索引之后,我们如何根据用户属性进行快速地匹配,找到满足条件,可以播放的广告呢?
3.1 用户请求范式
我们通常也用一个类文档的方式类描述应用用户属性条件,例如:
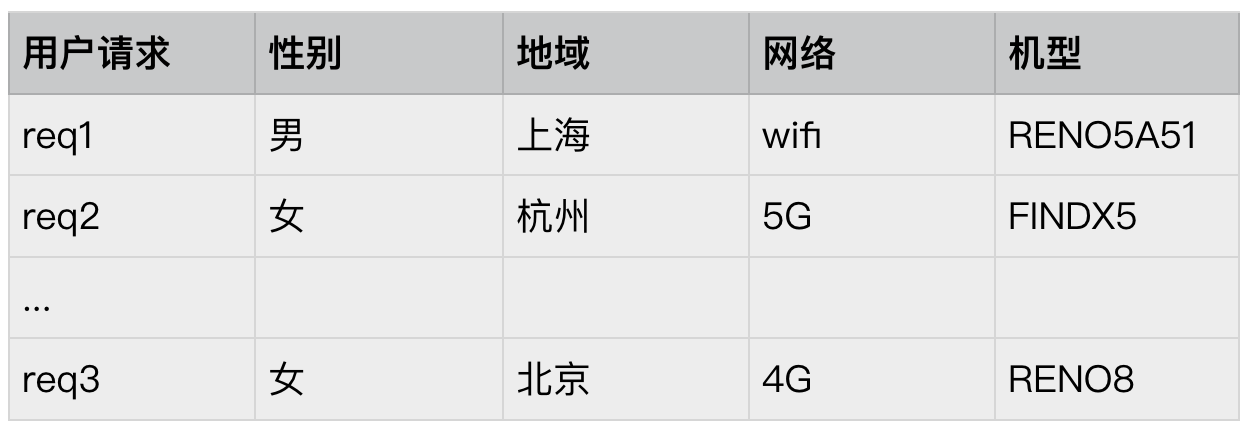
为连续的多个(attribute, value) 的二元组来表达,实际上我们也可以将其称为 assignments,或者叫 request assignments。
3.2 检索匹配范围
如 3.1 所述,request assignments 为一个多个(attribute, value) 二元组的列表。
令 n = request assignments 's size ,我们仅需要在 Level size <= n 的索引中检索符合条件的 Conjunction id。
举个例子:假如有 request assignments :{gender=M, City = SZ} , n = 2,因此,我们仅需要在 level size <= 2 的索引中进行查询。即 level 0, level 1, level 2
原因很简单,假如广告主创建了一个广告定向条件对应的 Conjunction size=3,也就是说要满足三个属性∈的条件才能够匹配。
例如:c5:Gender ∈ {M} ^ city ∈ {SZ} ^ network ∈ {WIFI,4G} |c5| = 3
一旦检索请求的属性数量小于 3,则无论如何也无法满足 c5 中要求定向的三个条件。
3.3 高效的 DNF 检索算法
在介绍《Indexing Boolean Expressions》中描述的高效的 DNF 检索算法之前,我们有几个点需要先了解一下,首先是我们需要知道当一个检索请求来了之后,哪些 Conjunction 是符合条件的?假如要进行暴力检索,应该会怎么做?
3.3.1 符合条件的 Conjunction
什么是符合条件的 Conjunction,对于一个析取范式的合取子句,即 xxx 且 xxx 且 xxx 来说,只有同时满足 3 个条件才算符合条件。由于“xxx”可能是∈ 也可能是∉,那么对于一个符合条件的 Conjunction 来说,需要保证所有∈的条件均满足,∉的条件均不能满足。
又由于,我们对 Conjunction size 的定义为∈条件的个数,那么最终,我们需要满足:
满足 ∈条件的个数 >=Conjunction size 且 满足 ∉条件的个数 <= 0 个。
3.3.2 暴力法找到符合条件的 Conjunction ID
为了找到,满足 ∈条件的个数 >=Conjunction size 且 满足 ∉条件的个数 <= 0 个 的 Conjunction 。我先用暴力法找到这些 Conjunction。
以 Level 2 中的 c2,c3,c4 为例

用一个大致的伪代码的表达一下

根据这个伪代码,假如我们的 reqAssignments 为

通过上文中 alg1 的计算可以得到如何下结果
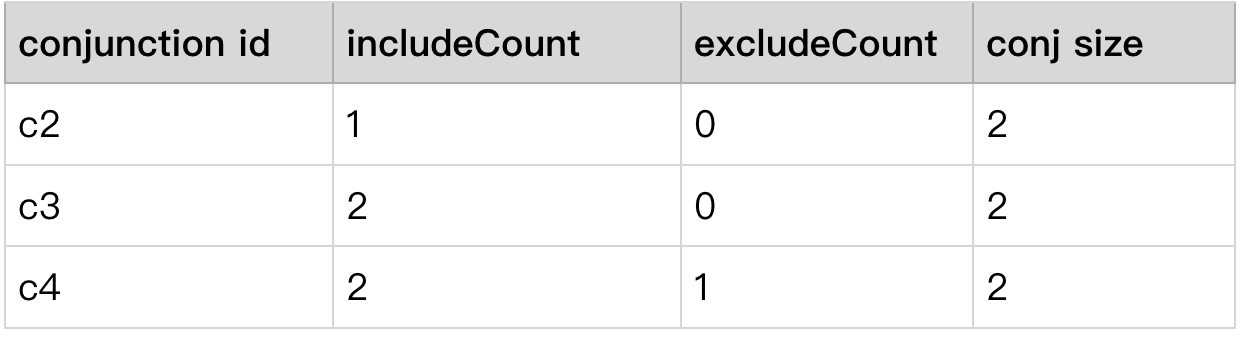
只有 c3 满足 includeCount >= conj size && excludeCount <= 0 的条件,即
满足 ∈条件的个数 >=Conjunction size 且 满足 ∉条件的个数 <= 0 个
由于我们的示例中 Conjunction 的数量非常少,通过这种方式来查询符合条件的 conj id 是比较快的。时间复杂度 O(n^2),当数据量大了之后这种方式并不高效。
3.3.3 DNF 检索算法
在了解到,暴力检索的时间复杂度过高,效率太低的问题之后,我们来具体介绍《Boolean expression indexing》中如何进行高效的 DNF 检索。
在 3.3.2 中我们介绍了暴力检索算法,可以发现,根本用不到 2.3.2 中建立的第一级倒排。直接遍历所有的 Conjunction 即可。那么当我们有了倒排之后,检索算法是如何做的?又能如何提高我们的检索速度呢。原文中给出的伪代码非常长,我们尽力通过简单易懂的流程图的方式进行拆分讲解。

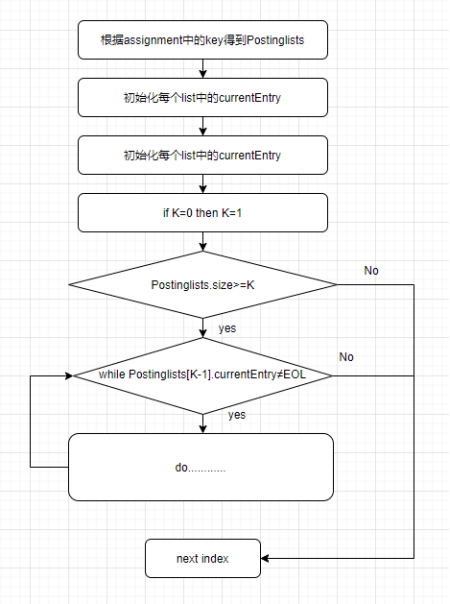
我们将整个流程分为预处理和循环计算两个部分。我们的 reqAssignments 仍然为例

由于我们的请求 reqAssignments size =3 ,所有 level 0 - level 3 均可以进行检索,我们以 Conjunction 数量最多的 level 2 进行举例
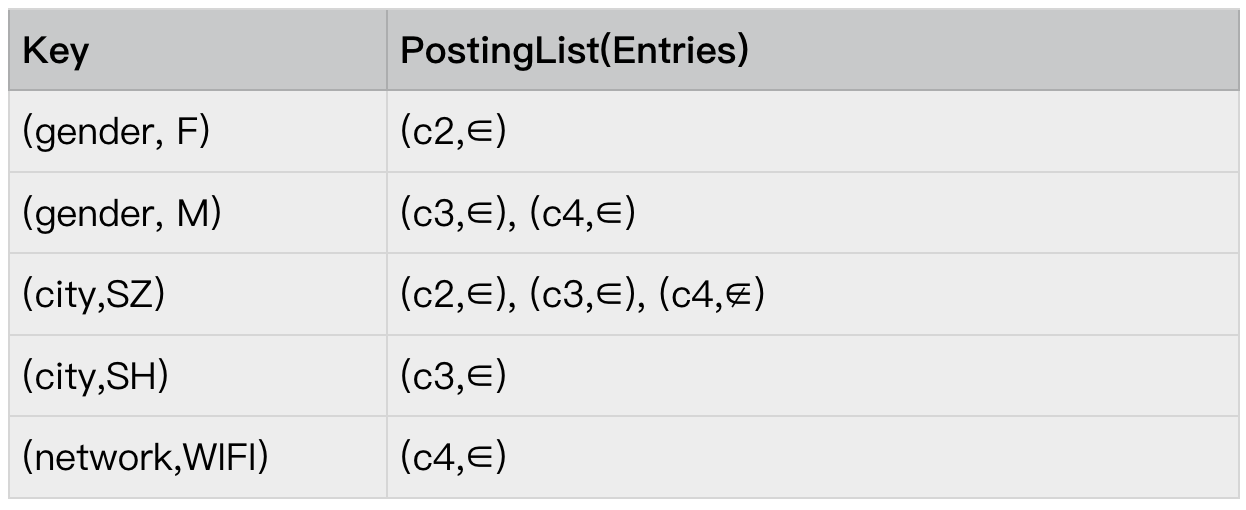
step1.预处理-初始化筛选 postingList
首先,我们需要根据 reqAssignments,找到需要所有的 postingList。逻辑很简单,
将 reqAssignments 的所有属性组织成 key,即(gender, M),(city,SZ),(network,WIFI)从 level 2 的索引中找到对应的 postingList
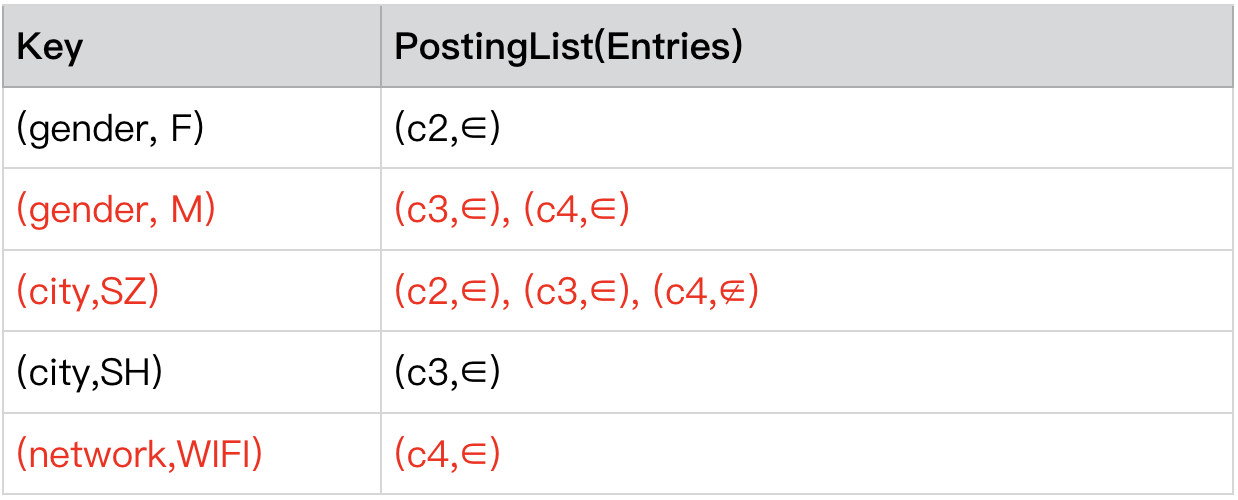
==============>

step2.预处理-初始化 postingLists
随后,我们将对这些需要进行计算的 postingList 进行初始化。首先我们将每一个 postingList 按 Conjunctionid 升序进行排序,当 Conjunctionid 相同时,∉<∈。

并将设置一个指针,初始阶段指向每个 list 第一个 entry,我们用下划线表示指针的位置,该指针指向的 entry,称为该 list 的 currentEntry
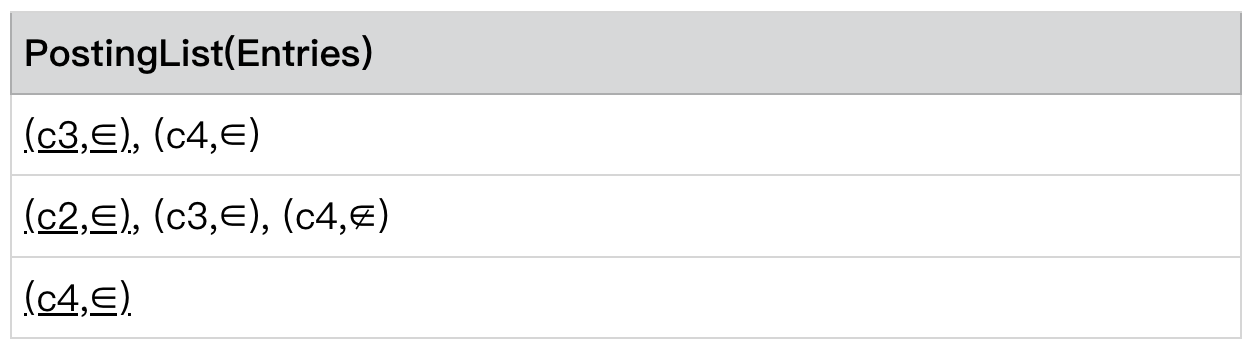
最终我们 PostingList 之间的排序则按照 currentEntry 的大小进行排序,排序的规则与 PostingList 内部的排序规则相同。

整体的排布类似如下图片,小值集中在左上角。
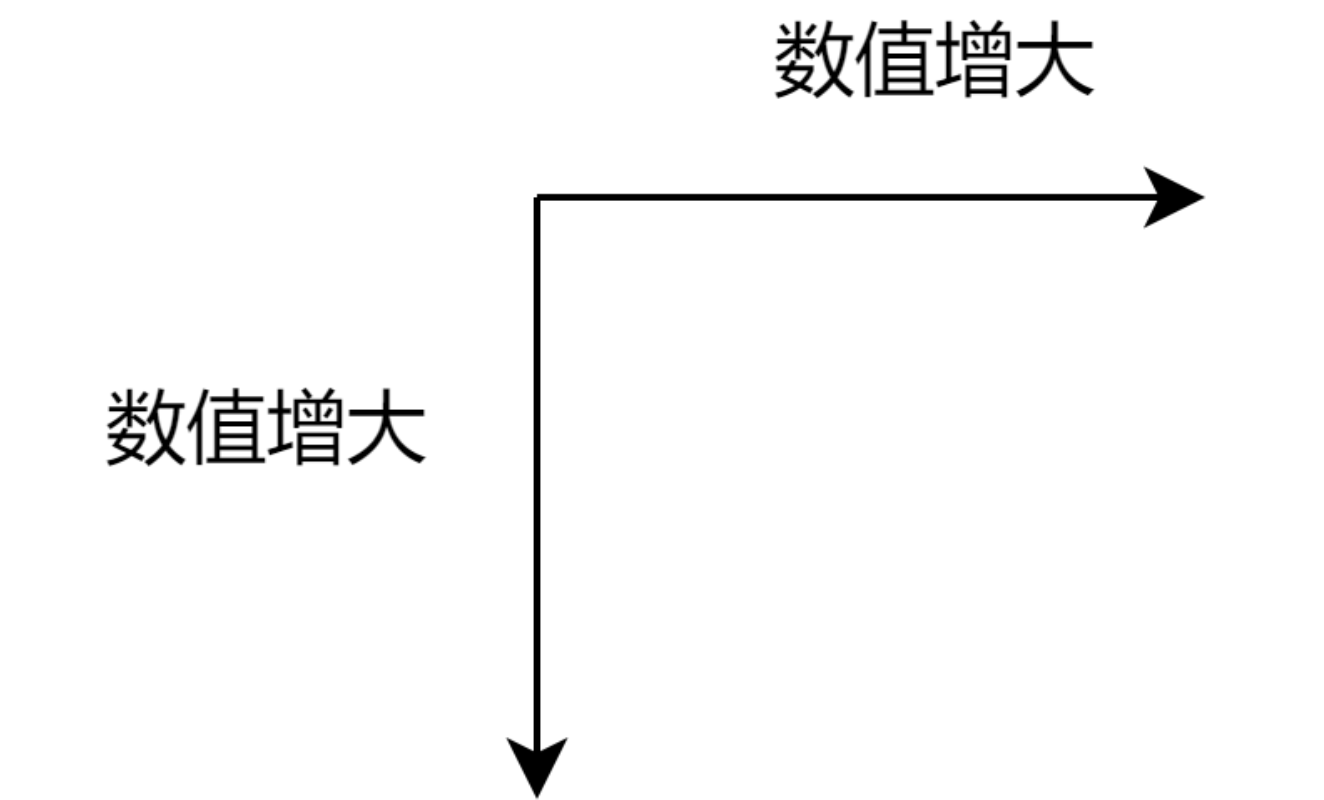
step3.循环阶段
随后我们进入到循环阶段,从预处理后的 PostingLists 找到符合条件的 Conjunction。整体流程如下图所示,我们可以发现实际上只关注第 0 和第 K-1 个 PostingLists 的 currentEntry.id 以及 predicate 即可找到所有符合条件的 Conjunction。
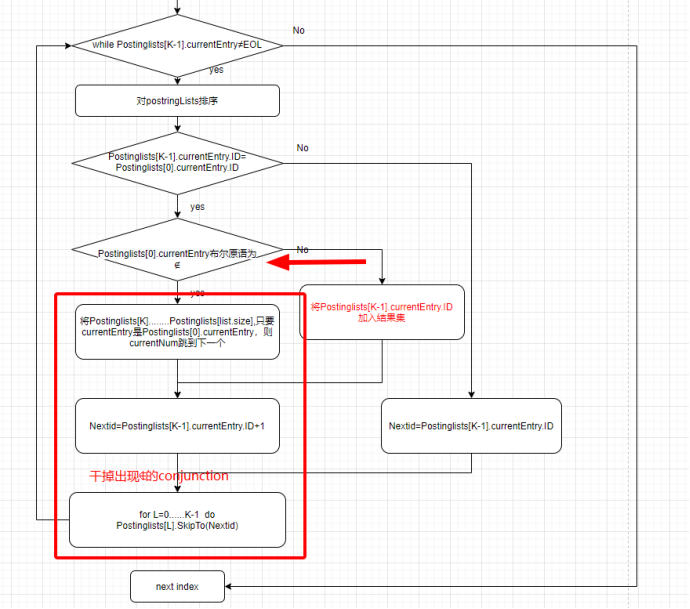
情况 1:不相等
将第 1 到第 K 行 skip to 第 K-1 行首位的 Conjunction id 的位置。并且重新按 currentEntry 排序。还是以 level 2 为例。
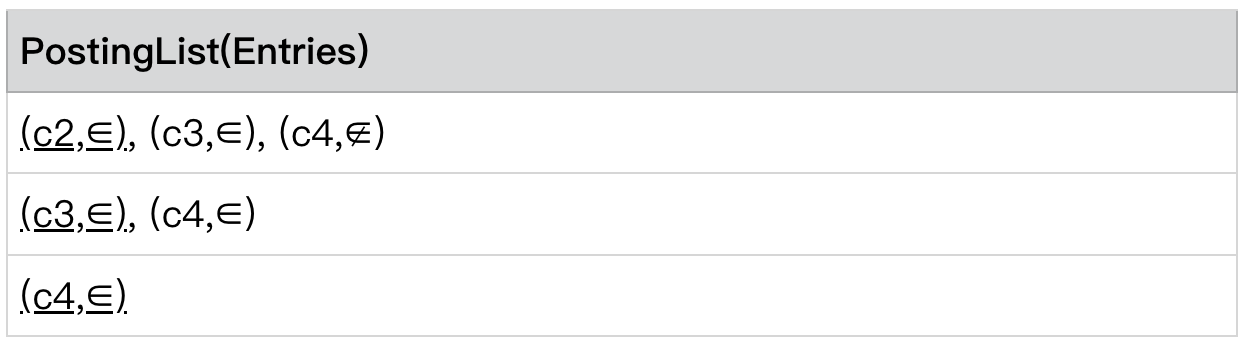
还是以 level 2 为例,
PostingLists[0] .currentEntry= (c2,∈)
PostingLists[level - 1] .currentEntry= (c3,∈)
c2 ≠c3
将第 1 到第 K-1 行 skip to 第 k-1 行 currentEntry.id 的位置。并且重新按 currentEntry 排序。

为什么我们不真正地删除掉(c2,∈) 这个 entry,实际上这是各工程问题。我们并不会毁坏原始的索引结构,而是通过指针的方式跳过这些不需要关注的 entry。
情况 2:相等 且 PostingLists[0] .predicate = ∈
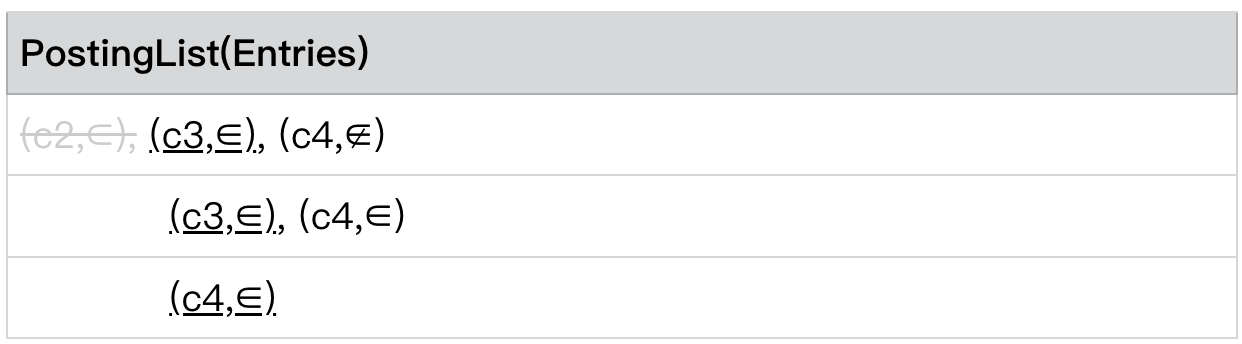
此时我们发现,
PostingLists[0] .currentEntry= (c3,∈)
PostingLists[level - 1] .currentEntry= (c3,∈)
且 PostingLists[0] .currentEntry.predicate = ∈ ,
则 c3 是我们认为满足条件的 Conjunction,我们将其加入最终的候选集中。并将所有 c3 的 entry skip to 到 next entry。

情况 3:相等 且 PostingLists[0] .predicate = ∉
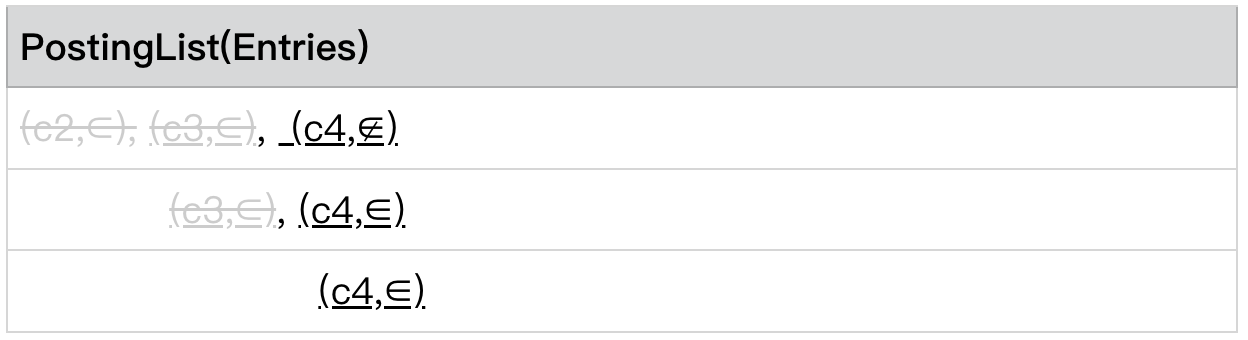
此时我们发现,
PostingLists[0] .currentEntry= (c4,∉)
PostingLists[level - 1] .currentEntry= (c4,∈)
PostingLists[0] .currentEntry.predicate = ∉
则 c4 是我们认为不满足条件的 Conjunction,并将所有 c4 的 entry skip to 到 next entry。
情况 4:PostingLists[level - 1] .currentEntry=NULL 跳出循环
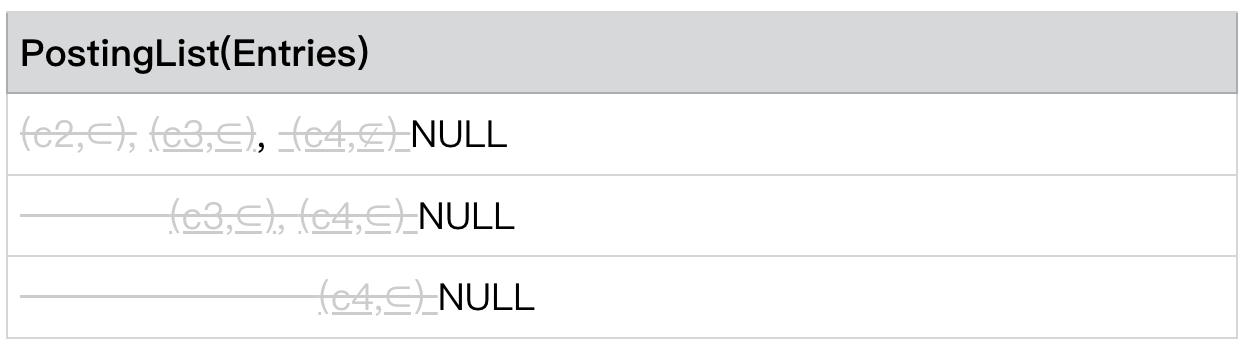
PostingLists[level - 1] .currentEntry=NULL
此时跳出循环,该 level 的检索结束。
4.召回系统中的检索模块
在介绍完索引的结果和检索的算法后,我们再来整体看一下检索模块在召回系统中的大致应用。

step 0 :召回在请求检索前,会访问用户画像,将用户画像中的信息组织成 request assignments 的范式,请求检索模块。
step 1 :检索中控将 request assignments 输入第一级倒排中,通过我们第三节中描述的 DNF 检索算法计算出满足条件的 Conjunction id 列表
step 2 :检索中控将 Conjunction id 列表输入第二级倒排中,通过 hash 的方式找到所有 Conjunction ID 对应的广告列表返回给召回。
5.写在最后
目前,广告业界,检索的设计并不是一个通解。索引的复杂度与支持的布尔语句基本上正相关,所以通常我们会基于业务场景决定使用的索引结构。
此外,随着向量检索+布尔检索的多路检索模式的普及,以及去定向化的趋势,布尔检索不再是广告引擎中唯一决定广告是否播放的原因。
引用
1.析取范式定义:https://zh.wikipedia.org/wiki/%E6%9E%90%E5%8F%96%E8%8C%83%E5%BC%8F
2.Indexing Boolean Expressions https://theory.stanford.edu/~sergei/papers/vldb09-indexing.pdf
3.广告召回系统的演进https://zhuanlan.zhihu.com/p/110112102
4.美团广告实时索引的设计与实现https://tech.meituan.com/2018/05/11/adp-rtidx-ls.html





