本文最初发布于 towards data science 网站,经原作者授权由 InfoQ 中文站翻译并分享。
不变风险最小化(Invariant Risk Minimization,IRM)是一种激动人心的新型学习范式,可帮助预测模型的泛化水平超越训练数据的局限。它由 Facebook 的研究人员开发,并在 2020 年的一篇论文中做了介绍。这种方法可以添加到几乎任何建模框架中,但它最适合的是利用大量数据的黑盒模型(各种神经网络及它们的变体)。
本文中,我们就来深入了解一番。
技术总览
在高层次上,IRM 是一种学习范式,它试图学习因果关系而不是相关关系。通过开发训练环境和结构化数据样本等手段,我们可以尽可能提高准确性,同时保证预测变量的不变性。既适合我们的数据,又在各种环境中保持不变的预测变量被用作最终模型的输出。
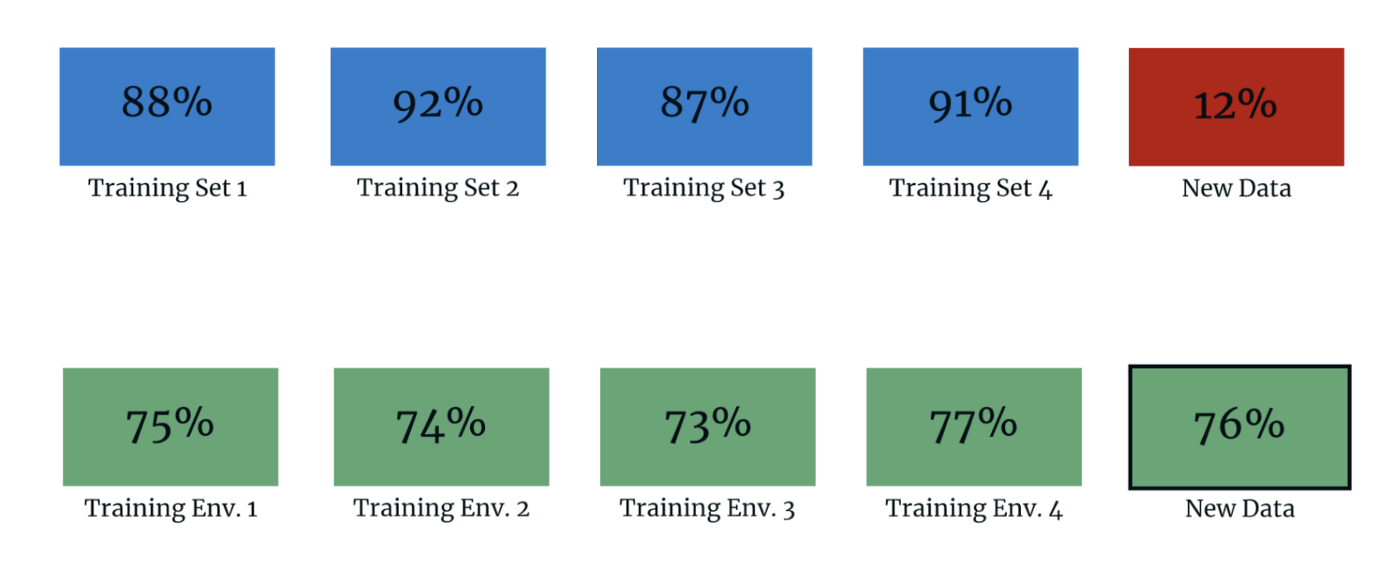
图 1:4-foldCV(顶部)与不变风险最小化(IRM)(底部)的理论性能对比。这些值是从论文中的模拟推断出来的。
第 1 步:开发你的环境集。我们没有重新整理数据并假设它们是 IID,而是使用与数据选择过程相关的知识来开发多种采样环境。例如,对于一个解析图像中文本的模型,我们的训练环境可以按编写文本的作者来分组。
第 2 步:最小化跨环境损失。开发环境之后,我们会拟合近似不变的预测变量并优化我们跨环境的准确性。更多信息请参阅后文。
第 3 步:更好地泛化!风险不变最小化方法表现出比传统学习范式更高的分布外(out-of-distribution,OOD)准确性。
到底发生了什么事情?
我们先停一下,来了解风险不变最小化的实际工作机制。
预测模型是做什么的?
首先,预测模型的目的是泛化,也就是在没见过的数据上也获得良好的表现。我们将没见过的数据称为分布外(OOD)。
为了模拟新数据,业界引入了多种方法(如交叉验证)。尽管这种方法比简单的训练集要好,但我们仍然受限于观察到的数据。那么,你能确保这个模型会泛化吗?
嗯,一般来说你是不能的。
对于一些有着明确定义的问题来说(其中你对数据生成机制有着很好的理解),我们可以确信我们的数据样本代表了总体。但对于大多数应用类型而言我们没法这样肯定。
举一个论文中引用的例子。我们想要判断一张图里的动物是牛还是骆驼。
为此,我们使用交叉验证训练一个二元分类器,并观察到模型在我们的测试数据上获得了很高的精度。很好!
然而,经过更多的探索,我们发现我们的分类器只是简单地使用背景的颜色来判断图像是牛还是骆驼;当一头奶牛被放置在沙色背景中时,模型总会认为它是一头骆驼,反之亦然。
现在,我们是否可以假设人们总是只在牧场上观察到奶牛,而只在沙漠中观察到骆驼呢?
显然不行。虽然这是一个很小的例子,但我们可以看到类似的情况也会影响更复杂和更重要的模型。
为什么目前的方法不够用?
在深入研究解决方案之前,我们先进一步了解为什么流行的训练/测试学习范式是不够用的。
经典的训练/测试范式在论文中被称为经验风险最小化(Empirical Risk Minimization ,ERM)。在 ERM 中,我们将数据汇集到训练/测试集中,在所有特征上训练模型,使用测试集进行验证,并返回具有最佳测试(样本外)准确性的拟合模型。一个例子是 50/50 的训练测试拆分。
现在,为了理解为什么 ERM 不能很好地泛化,我们来分别看一下它的三个主要假设:
我们的数据是独立同分布的(IID)。
随着我们收集更多数据,样本大小 n 与显著特征数量之间的比率应该会降低。
只有存在具有完美训练准确度的可实现(可构建)模型时,才会出现完美的测试准确度。
乍一看,这三个假设似乎都成立。但实际情况往往相反。
看看我们的第一个假设,我们的数据几乎从来都不是真正的 IID。在实践中,收集数据时几乎总是会引入数据点之间的关系。例如,沙漠中骆驼的所有图像都必须在世界的某些地方拍摄。
现在有很多数据“非常”IID 的情况,但重要的是,要批判性地思考你的数据收集是否以及如何引入偏见。
假设 #1:如果我们的数据不是 IID,那么第一个假设就失效了,我们不能随机打乱我们的数据。重要的是要考虑你的数据生成机制是否会引入偏见。
对于我们的第二个假设,如果我们是对因果关系建模,我们会期望显著特征的数量在一定数量的观察之后保持基本稳定。换句话说,随着我们收集更多高质量的数据,我们将能够找出真正的因果关系并完美地映射它们,因此更多的数据不会提高我们的准确性。
但对于 ERM 来说这种情况很少发生。由于我们无法确定某种关系是否是因果的,因此更多的数据通常会拟合出更多虚假的相关性。这种现象被称为偏见-方差权衡。
假设 #2:当使用 ERM 进行拟合时,显著特征的数量可能会随着我们样本量的增加而增长,从而让我们的第二个假设无效。
最后,我们的第三个假设只是说明我们有能力构建一个“完美”的模型。如果我们缺乏数据或强大的建模技术,这个假设将无效。然而,除非我们知道这是做不到的,否则我们总是假设它是可行的。
假设 #3:我们假设足够大的数据集可以实现最优模型,因此假设 #3 成立。
论文中也讨论了一些非 ERM 方法,但由于各种原因,它们也存在不足。
解决方案:不变风险最小化
论文所提出的解决方案称为不变风险最小化(IRM),它克服了上面列出的所有问题。IRM 是一种学习范式,可以从多个训练环境中估计因果预测变量。而且,因为我们是从不同的数据环境中学习的,我们更有可能泛化到新的 OOD 数据上。
如何做到这一点呢?我们利用了因果关系依赖于不变性的概念。
回到我们的例子,我们看到的 95%的图像中,奶牛的背景是草地,而骆驼的背景是沙漠,所以如果我们拟合背景的颜色,将达到 95%的准确率。从表面上看,这是一个非常合适的选项。
然而,随机对照试验中有一个叫做反事实的核心概念,说的是如果我们看到了一个假设的反例,我们就可以推倒这个假设了。因此,只要我们在沙漠中看到了一头奶牛,我们就可以得出结论,沙漠背景不会必然关联骆驼。
虽然严格的反事实有点苛刻,但我们可以严厉惩罚我们的模型在给定环境中预测错误的实例,从而将这个概念构建到我们的损失函数中。
例如,考虑一组环境,其中每个环境对应一个国家。假设 9/10 的环境中奶牛生活在牧场,而骆驼生活在沙漠,但在第 10 类环境中这种模式反过来了。当我们在第 10 个环境中训练并观察到许多反例时,模型了解到单从背景不足以打出牛或骆驼的标签,因此降低了这个预测变量的显著性。
方法
我们已经看明白了 IRM 的含义,现在我们进入数学世界,学习该如何实现它。
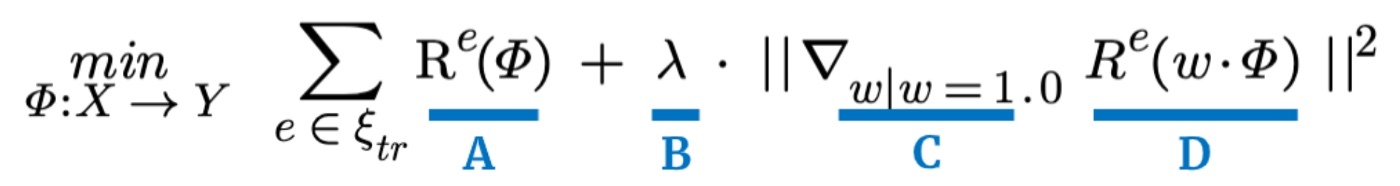
图 2:最小化表达式
图 2 展示了我们的优化表达式。正如总和所示,我们希望在所有训练环境中最小化总和值。
进一步细分,“A”项代表我们在给定训练环境中的预测准确性,其中 phi(𝛷)代表数据变换,例如一个对数或核心变换到更高维度。R 表示我们模型在给定环境 e 下的风险函数。请注意,风险函数只是损失函数的平均值。一个经典的例子是均方误差(MSE)。
“B”项只是一个正数,用于缩放我们的不变性项。还记得我们说过严格的反事实可能太苛刻了吗?这里我们可以衡量这种苛刻的程度。如果 lambda(λ)为 0,我们就不关心不变性,只需优化准确性。如果λ很大,我们非常关心不变性并相应地给出惩罚。
最后,“C”和“D”项代表我们的模型在训练环境中的不变性。我们不需要深入研究这一术语,但简而言之,我们的“C”项是线性分类器 w 的梯度向量,默认值为 1。“D”是该线性分类器的风险 w 乘以我们的数据转换(𝛷)。整个项是梯度向量的平方距离。
论文详细介绍了这些术语,如果你好奇,请查看第 3 部分。
总之,“A”是我们模型的准确性,“B”是衡量我们对不变性的关注程度的正数,“C”“D”是我们模型的不变性。如果我们最小化这个表达式,我们应该能找到一个模型,其只能拟合在我们的训练环境中发现的因果效应。
IRM 后续发展
不幸的是,本文介绍的 IRM 范式仅适用于线性情况。将我们的数据变换到高维空间可以获得有效的线性模型,但一些关系从根本上就是非线性的。论文作者将非线性情况留给了将来的研究。
如果你想跟踪这一研究,可以查看以下作者的成果:Martin Arjovsky、León Buttou、Ishaan Gulrajani和David Lopez-Paz。
这就是我们的方法,还不错吧?
实现注意事项
这里有一个 PyTorch包。
IRM 最适合未知的因果关系。如果存在已知关系,你应该在模型结构中考虑它们。一个著名的例子是卷积神经网络(CNN)的卷积。
IRM 在无监督模型和强化学习方面具有很大的潜力。模型公平性也是一个有趣的应用。
优化非常复杂,因为有两个最小化项。论文概述了一种使优化凸出的变换,但仅限于线性情况。
IRM 对轻度模型错误定义具有稳健性,因为它在训练环境的协方差方面是可微的。因此,虽然“完美”模型是理想的,但最小化表达式对小的人为错误具有弹性。
原文链接:
https://towardsdatascience.com/how-to-make-deep-learning-models-to-generalize-better-3341a2c5400c





