深入浅出 Tensorflow（四）：卷积神经网络

2017 年 2 月 16 日，Google 正式对外发布 Google TensorFlow 1.0 版本，并保证本次的发布版本 API 接口完全满足生产环境稳定性要求。这是 TensorFlow 的一个重要里程碑，标志着它可以正式在生产环境放心使用。在国内，从 InfoQ 的判断来看，TensorFlow 仍处于创新传播曲线的创新者使用阶段，大部分人对于 TensorFlow 还缺乏了解，社区也缺少帮助落地和使用的中文资料。InfoQ 期望通过深入浅出 TensorFlow 系列文章能够推动 Tensorflow 在国内的发展。欢迎加入 QQ 群（群号：183248479）深入讨论和交流。下面为本系列的前三篇文章：

深入浅出Tensorflow（一）：深度学习及TensorFlow 简介

深入浅出TensorFlow（二）：TensorFlow 解决MNIST 问题入门

深入浅出Tensorflow（三）：训练神经网络模型的常用方法

本文为第四篇文章，将会介绍卷积神经网络，通过与传统算法的对比、卷积神经网络的结构分析等方面来介绍卷积神经网络模型，并给出通过TensorFlow 在MNIST 数据集上实现卷积神经网络的方法。

卷积神经网络简介

斯坦福大学（Stanford University）李飞飞（Feifei Li）教授带头整理的ImageNet 是图像识别领域非常有名的数据集。在ImageNet 中，将近1500 万图片被关联到了WordNet 的大约20000 个名词同义词集上。ImageNet 每年都举办图像识别相关的竞赛（ImageNet Large Scale Visual Recognition Challenge，ILSVRC），其中最有名的就是ILSVRC2012 图像分类数据集。ILSVRC2012 图像分类数据集包含了来自1000 个类别的120 万张图片，其中每张图片属于且只属于一个类别。因为ILSVRC2012 图像分类数据集中的图片是直接从互联网上爬取得到的，图片的大小从几千字节到几百万字节不等。

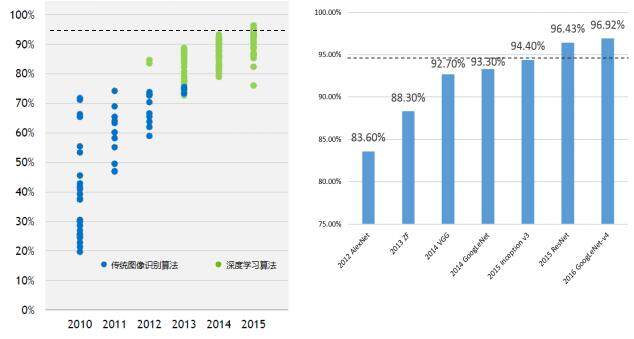
图1 不同算法在ImageNet ILSVRC2012 图像分类数据集上的正确率

图1 给出了不同算法在ImageNet 图像分类数据集上的top-5 正确率。top-N 正确率指的是图像识别算法给出前N 个答案中有一个是正确的概率。在图像分类问题上，很多学术论文都将前N 个答案的正确率作为比较的方法，其中N 的取值一般为3 或5。从图1 中可以看出，在ImageNet 问题上，基于卷积神经网络的图像识别算法可以远远超过人类的表现。在图1 的左侧对比了传统算法与深度学习算法的正确率。从图中可以看出，深度学习，特别是卷积神经网络，给图像识别问题带来了质的飞跃。2013 年之后，基本上所有的研究都集中到了深度学习算法上。

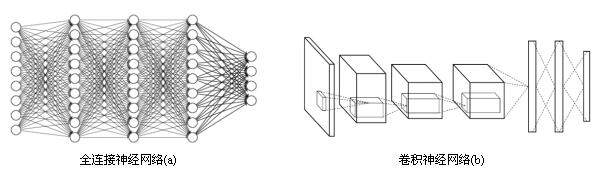
图2 全连接神经网络与卷积神经网络结构示意图

在前面的文章中所介绍的神经网络每两层之间的所有结点都是有边相连的，所以我们称这种网络结构为全连接层网络结构。图2 显示了全连接神经网络与卷积神经网络的结构对比图。虽然图2 中显示的全连接神经网络结构和卷积神经网络的结构直观上差异比较大，但实际上它们的整体架构是非常相似的。从图2 中可以看出，卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样，卷积神经网络中的每一个节点都是一个神经元。在全连接神经网络中，每相邻两层之间的节点都有边相连，于是一般会将每一层全连接层中的节点组织成一列，这样方便显示连接结构。而对于卷积神经网络，相邻两层之间只有部分节点相连，为了展示每一层神经元的维度，一般会将每一层卷积层的节点组织成一个三维矩阵。

除了结构相似，卷积神经网络的输入输出以及训练流程与全连接神经网络也基本一致。以图像分类为例，卷积神经网络的输入层就是图像的原始像素，而输出层中的每一个节点代表了不同类别的可信度。这和全连接神经网络的输入输出是一致的。在TensorFlow 中训练一个卷积神经网络的流程和训练一个全连接神经网络没有任何区别。卷积神经网络和全连接神经网络的唯一区别就在于神经网络中相邻两层的连接方式。

使用全连接神经网络处理图像的最大问题在于全连接层的参数太多。对于MNIST 数据，每一张图片的大小是28×28×1，其中28×28 为图片的大小，*1 表示图像是黑白的，只有一个色彩通道。假设第一层隐藏层的节点数为500 个，那么一个全链接层的神经网络将有28×28×500+500=392500 个参数。当图片更大时，比如在Cifar-10 数据集中，图片的大小为32×32×3，其中32×32 表示图片的大小，×3 表示图片是通过红绿蓝三个色彩通道（channel）表示的。这样输入层就有3072 个节点，如果第一层全连接层仍然是500 个节点，那么这一层全链接神经网络将有3072×500+50 约等于150 万个参数。参数增多除了导致计算速度减慢，还很容易导致过拟合问题。所以需要一个更合理的神经网络结构来有效地减少神经网络中参数个数。卷积神经网络就可以达到这个目的。

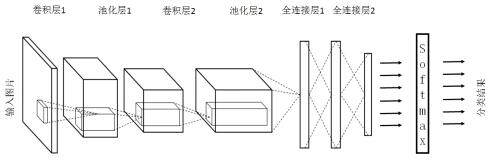
图3 用于图像分类问题的一种卷积神经网络架构图

图3 给出了一个更加具体的卷积神经网络架构图。在卷积神经网络的前几层中，每一层的节点都被组织成一个三维矩阵。比如处理Cifar-10 数据集中的图片时，可以将输入层组织成一个32*32*3 的三维矩阵。图3 中虚线部分展示了卷积神经网络的一个连接示意图，从图中可以看出卷积神经网络中前几层中每一个节点只和上一层中部分的节点相连。卷积神经网络的具体连接方式将在下文中介绍。

< 卷积层网络结构 >

图 4 中显示了卷积层神经网络结构中最重要的部分，这个部分被称之为过滤器（filter）或者内核（kernel）。因为 TensorFlow 文档中将这个结构称之为过滤器（filter），所以我们将统称这个结构为过滤器。如图 4 所示，过滤器可以将当前层神经网络上的一个子节点矩阵转化为下一层神经网络上的一个单位节点矩阵。单位节点矩阵指的是一个长和宽都为 1，但深度不限的节点矩阵。

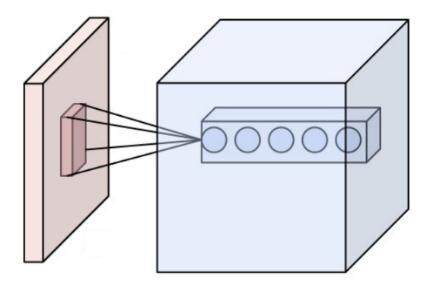
图 4 卷积层过滤器（filter）结构示意图

在一个卷积层中，过滤器所处理的节点矩阵的长和宽都是由人工指定的，这个节点矩阵的尺寸也被称之为过滤器的尺寸。常用的过滤器尺寸有 3×3 或 5×5。因为过滤器处理的矩阵深度和当前层神经网络节点矩阵的深度是一致的，所以虽然节点矩阵是三维的，但过滤器的尺寸只需要指定两个维度。过滤器中另外一个需要人工指定的设置是处理得到的单位节点矩阵的深度，这个设置称为过滤器的深度。注意过滤器的尺寸指的是一个过滤器输入节点矩阵的大小，而深度指的是输出单位节点矩阵的深度。如图 4 所示，左侧小矩阵的尺寸为过滤器的尺寸，而右侧单位矩阵的深度为过滤器的深度。

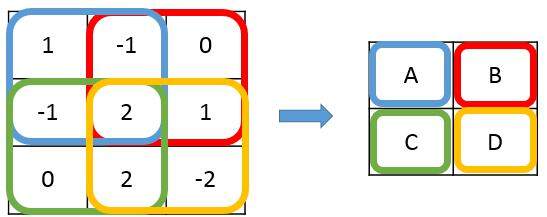
图 5 卷积层前向传播过程示意图

在图 5 中，只讲解了移动过滤器的方式，没有涉及到过滤器中的参数如何设定。在卷积神经网络中，每一个卷积层中使用的过滤器中的参数都是一样的。这是卷积神经网络一个非常重要的性质。从直观上理解，共享过滤器的参数可以使得图像上的内容不受位置的影响。以 MNIST 手写体数字识别为例，无论数字“1”出现在左上角还是右下角，图片的种类都是不变的。因为在左上角和右下角使用的过滤器参数相同，所以通过卷积层之后无论数字在图像上的哪个位置，得到的结果都一样。

共享每一个卷积层中过滤器中的参数可以巨幅减少神经网络上的参数。以 Cifar-10 问题为例，输入层矩阵的维度是 32×32×3。假设第一层卷积层使用尺寸为 5×5，深度为 16 的过滤器，那么这个卷积层的参数个数为 5×5×3×16+16=1216 个。上文提到过，使用 500 个隐藏节点的全连接层将有 150 万个参数。相比之下，卷积层的参数个数要远远小于全连接层。而且卷积层的参数个数和图片的大小无关，它只和过滤器的尺寸、深度以及当前层节点矩阵的深度有关。这使得卷积神经网络可以很好地扩展到更大的图像数据上。

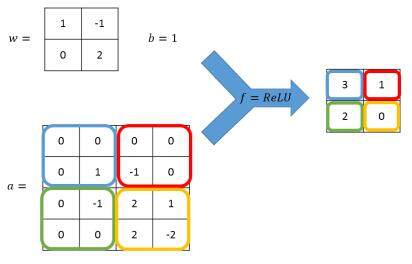
图 6 卷积层前向传播过程样例图

结合过滤器的使用方法和参数共享的机制，图 6 给出了使用了全 0 填充、移动步长为 2 的卷积层前向传播的计算流程。下面的公式给出了左上角格子取值的计算方法，其他格子可以依次类推。

 
ReLu（0×1+0×（-1）+0×0+1×2+1）=ReLu（3）=3

TensorFlow 对卷积神经网络提供了非常好的支持，下面的程序实现了一个卷积层的前向传播过程。从以下代码可以看出，通过 TensorFlow 实现卷积层是非常方便的。

 
# 通过 tf.get_variable 的方式创建过滤器的权重变量和偏置项变量。上面介绍了卷积层
# 的参数个数只和过滤器的尺寸、深度以及当前层节点矩阵的深度有关，所以这里声明的参数变
# 量是一个四维矩阵，前面两个维度代表了过滤器的尺寸，第三个维度表示当前层的深度，第四
# 个维度表示过滤器的深度。
filter_weight = tf.get_variable(
   'weights', [5, 5, 3, 16], 
   initializer=tf.truncated_normal_initializer(stddev=0.1))
# 和卷积层的权重类似，当前层矩阵上不同位置的偏置项也是共享的，所以总共有下一层深度个不
# 同的偏置项。本样例代码中 16 为过滤器的深度，也是神经网络中下一层节点矩阵的深度。
biases = tf.get_variable(
   'biases', [16], initializer=tf.constant_initializer(0.1))
 
# tf.nn.conv2d 提供了一个非常方便的函数来实现卷积层前向传播的算法。这个函数的第一个输
# 入为当前层的节点矩阵。注意这个矩阵是一个四维矩阵，后面三个维度对应一个节点矩阵，第一
# 维对应一个输入 batch。比如在输入层，input[0,:,:,:] 表示第一张图片，input[1,:,:,:] 
# 表示第二张图片，以此类推。tf.nn.conv2d 第二个参数提供了卷积层的权重，第三个参数为不
# 同维度上的步长。虽然第三个参数提供的是一个长度为 4 的数组，但是第一维和最后一维的数字
# 要求一定是 1。这是因为卷积层的步长只对矩阵的长和宽有效。最后一个参数是填充（padding）
# 的方法，TensorFlow 中提供 SAME 或是 VALID 两种选择。其中 SAME 表示添加全 0 填充，
# “VALID”表示不添加。
conv = tf.nn.conv2d(
   input, filter_weight, strides=[1, 1, 1, 1], padding='SAME')
 
# tf.nn.bias_add 提供了一个方便的函数给每一个节点加上偏置项。注意这里不能直接使用加
# 法，因为矩阵上不同位置上的节点都需要加上同样的偏置项。虽然下一层神经网络的大小为
# 2×2，但是偏置项只有一个数（因为深度为 1），而 2×2 矩阵中的每一个值都需要加上这个
# 偏置项。
bias = tf.nn.bias_add(conv, biases)
# 将计算结果通过 ReLU 激活函数完成去线性化。
actived_conv = tf.nn.relu(bias)

池化层网络结构

在卷积神经网络中，卷积层之间往往会加上一个池化层（pooling layer）。池化层可以非常有效地缩小矩阵的尺寸，从而减少最后全连接层中的参数。使用池化层既可以加快计算速度也有防止过拟合问题的作用。和卷积层类似，池化层前向传播的过程也是通过移动一个类似过滤器的结构完成的。不过池化层过滤器中的计算不是节点的加权和，而是采用更加简单的最大值或者平均值运算。使用最大值操作的池化层被称之为最大池化层（max pooling），这是被使用得最多的池化层结构。使用平均值操作的池化层被称之为平均池化层（average pooling）。

与卷积层的过滤器类似，池化层的过滤器也需要人工设定过滤器的尺寸、是否使用全 0 填充以及过滤器移动的步长等设置，而且这些设置的意义也是一样的。卷积层和池化层中过滤器移动的方式是相似的，唯一的区别在于卷积层使用的过滤器是横跨整个深度的，而池化层使用的过滤器只影响一个深度上的节点。所以池化层的过滤器除了在长和宽两个维度移动之外，它还需要在深度这个维度移动。下面的 TensorFlow 程序实现了最大池化层的前向传播算法。

 
# tf.nn. max_pool 实现了最大池化层的前向传播过程，它的参数和 tf.nn.conv2d 函数类似。
# ksize 提供了过滤器的尺寸，strides 提供了步长信息，padding 提供了是否使用全 0 填充。
pool = tf.nn.max_pool(actived_conv, ksize=[1, 3, 3, 1], 
                         strides=[1, 2, 2, 1], padding='SAME')

对比池化层和卷积层前向传播在 TensorFlow 中的实现，可以发现函数的参数形式是相似的。在 tf.nn.max_pool 函数中，首先需要传入当前层的节点矩阵，这个矩阵是一个四维矩阵，格式和 tf.nn.conv2d 函数中的第一个参数一致。第二个参数为过滤器的尺寸。虽然给出的是一个长度为 4 的一维数组，但是这个数组的第一个和最后一个数必须为 1。这意味着池化层的过滤器是不可以跨不同输入样例或者节点矩阵深度的。在实际应用中使用得最多的池化层过滤器尺寸为 [1,2,2,1] 或者 [1,3,3,1]。

tf.nn.max_pool 函数的第三个参数为步长，它和 tf.nn.conv2d 函数中步长的意义是一样的，而且第一维和最后一维也只能为 1。这意味着在 TensorFlow 中，池化层不能减少节点矩阵的深度或者输入样例的个数。tf.nn.max_pool 函数的最后一个参数指定了是否使用全 0 填充。这个参数也只有两种取值——VALID 或者 SAME，其中 VALID 表示不使用全 0 填充，SAME 表示使用全 0 填充。TensorFlow 还提供了 tf.nn.avg_pool 来实现平均池化层。tf.nn.avg_pool 函数的调用格式和 tf.nn.max_pool 函数是一致的。

LeNet-5 模型

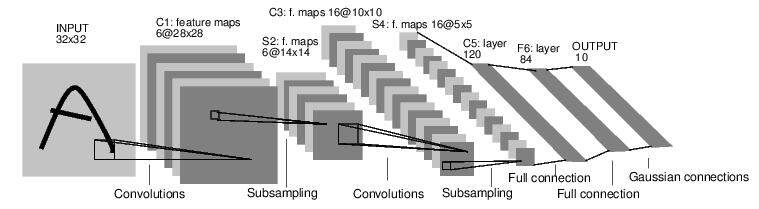
LeNet-5 模型是 Yann LeCun 教授于 1998 年在论文 _Gradient-based learning applied to document recognition_ 中提出的，它是第一个成功应用于数字识别问题的卷积神经网络。在 MNIST 数据集上，LeNet-5 模型可以达到大约 99.2% 的正确率。LeNet-5 模型总共有 7 层，图 7 展示了 LeNet-5 模型的架构。

(点击放大图像)

图 7 LeNet-5 模型结构图。

在下面的篇幅中将详细介绍 LeNet-5 模型每一层的结构。论文 _GradientBased Learning Applied to Document Recognition_ 提出的 LeNet-5 模型中，卷积层和池化层的实现与上文中介绍的 TensorFlow 的实现有细微的区别，这里不过多的讨论具体细节，而是着重介绍模型的整体框架。

第一层，卷积层

这一层的输入就是原始的图像像素，LeNet-5 模型接受的输入层大小为 32×32×1。第一个卷积层过滤器的尺寸为 5×5，深度为 6，不使用全 0 填充，步长为 1。因为没有使用全 0 填充，所以这一层的输出的尺寸为 32-5+1=28，深度为 6。这一个卷积层总共有 5×5×1×6+6=156 个参数，其中 6 个为偏置项参数。因为下一层的节点矩阵有 28×28×6=4704 个节点，每个节点和 5×5=25 个当前层节点相连，所以本层卷积层总共有 4704×（25+1）=122304 个连接。

第二层，池化层

这一层的输入为第一层的输出，是一个 28×28×6 的节点矩阵。本层采用的过滤器大小为 2×2，长和宽的步长均为 2，所以本层的输出矩阵大小为 14×14×6。原始的 LeNet-5 模型中使用的过滤器和本文中介绍的有些细微差别，这里不做具体介绍。

第三层，卷积层

本层的输入矩阵大小为 14×14×6，使用的过滤器大小为 5×5，深度为 16。本层不使用全 0 填充，步长为 1。本层的输出矩阵大小为 10×10×16。按照标准的卷积层，本层应该有 5×5×6×16+16=2416 个参数，10×10×16×（25+1）=41600 个连接。

第四层，池化层

本层的输入矩阵大小为 10×10×16，采用的过滤器大小为 2×2，步长为 2。本层的输出矩阵大小为 5×5×16。

第五层，全连接层

本层的输入矩阵大小为 5×5×16，在 LeNet-5 模型的论文中将这一层称为卷积层，但是因为过滤器的大小就是 5×5，所以和全连接层没有区别，在之后的 TensorFlow 程序实现中也会将这一层看成全连接层。如果将 5×5×16 矩阵中的节点拉成一个向量，那么这一层和在第四章中介绍的全连接层输入就一样了。本层的输出节点个数为 120，总共有 5×5×16×120+120=48120 个参数。

第六层，全连接层

本层的输入节点个数为 120 个，输出节点个数为 84 个，总共参数为 120×84+84=10164 个。

第七层，全连接层

本层的输入节点个数为 84 个，输出节点个数为 10 个，总共参数为 84×10+10=850 个。

上面介绍了 LeNet-5 模型每一层结构和设置，下面给出一个 TensorFlow 的程序来实现一个类似 LeNet-5 模型的卷积神经网络来解决 MNIST 数字识别问题。通过 TensorFlow 训练卷积神经网络的过程和第五章中介绍的训练全连接神经网络是完全一样的。损失函数的计算、反向传播过程的实现都可以复用上一篇中给出的 mnist_train.py 程序。唯一的区别在于因为卷积神经网络的输入层为一个三维矩阵，所以需要调整一下输入数据的格式：

 
# 调整输入数据 placeholder 的格式，输入为一个四维矩阵。
x = tf.placeholder(tf.float32, [
             BATCH_SIZE,                     # 第一维表示一个 batch 中样例的个数。
             mnist_inference.IMAGE_SIZE,    # 第二维和第三维表示图片的尺寸。
             mnist_inference.IMAGE_SIZE,                 
             mnist_inference.NUM_CHANNELS], # 第四维表示图片的深度，对于 RBG 格
                                                  #式的图片，深度为 5。
         name='x-input')
…
 
# 类似地将输入的训练数据格式调整为一个四维矩阵，并将这个调整后的数据传入 sess.run 过程。
reshaped_xs = np.reshape(xs, (BATCH_SIZE, 
                                   mnist_inference.IMAGE_SIZE, 
                                   mnist_inference.IMAGE_SIZE, 
                                   mnist_inference.NUM_CHANNELS))

在调整完输入格式之后，只需要在程序 mnist_inference.py 中实现类似 LeNet-5 模型结构的前向传播过程即可。下面给出了修改后的 mnist_infernece.py 程序。

 
# -*- coding: utf-8 -*-
import tensorflow as tf
 
# 配置神经网络的参数。
INPUT_NODE = 784  
OUTPUT_NODE = 10
 
IMAGE_SIZE = 28
NUM_CHANNELS = 1
NUM_LABELS = 10
 
# 第一层卷积层的尺寸和深度。
CONV1_DEEP = 32
CONV1_SIZE = 5
# 第二层卷积层的尺寸和深度。
CONV2_DEEP = 64
CONV2_SIZE = 5
# 全连接层的节点个数。
FC_SIZE = 512
 
# 定义卷积神经网络的前向传播过程。这里添加了一个新的参数 train，用于区分训练过程和测试
# 过程。在这个程序中将用到 dropout 方法，dropout 可以进一步提升模型可靠性并防止过拟合，
# dropout 过程只在训练时使用。
def inference(input_tensor, train, regularizer):
# 声明第一层卷积层的变量并实现前向传播过程。这个过程和 6.3.1 小节中介绍的一致。
# 通过使用不同的命名空间来隔离不同层的变量，这可以让每一层中的变量命名只需要
# 考虑在当前层的作用，而不需要担心重名的问题。和标准 LeNet-5 模型不大一样，这里
# 定义的卷积层输入为 28×28×1 的原始 MNIST 图片像素。因为卷积层中使用了全 0 填充，
# 所以输出为 28×28×32 的矩阵。
       with tf.variable_scope('layer1-conv1'):
      conv1_weights = tf.get_variable(
          "weight",  [CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_DEEP], 
          initializer=tf.truncated_normal_initializer(stddev=0.1)) 
      conv1_biases = tf.get_variable(
          "bias", [CONV1_DEEP], initializer=tf. constant_initializer(0.0))  
 
      # 使用边长为 5，深度为 32 的过滤器，过滤器移动的步长为 1，且使用全 0 填充。
      conv1 = tf.nn.conv2d(
          input_tensor, conv1_weights, 
          strides=[1, 1, 1, 1], padding='SAME')
      relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))
   
  # 实现第二层池化层的前向传播过程。这里选用最大池化层，池化层过滤器的边长为 2，
  # 使用全 0 填充且移动的步长为 2。这一层的输入是上一层的输出，也就是 28×28×32
  # 的矩阵。输出为 14×14×32 的矩阵。
  with tf.name_scope('layer2-pool1'):
      pool1 = tf.nn.max_pool(
          relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
   
  # 声明第三层卷积层的变量并实现前向传播过程。这一层的输入为 14×14×32 的矩阵。
  # 输出为 14×14×64 的矩阵。
  with tf.variable_scope('layer3-conv2'):
      conv2_weights = tf.get_variable(
          "weight", [CONV2_SIZE, CONV2_SIZE, CONV1_DEEP, CONV2_DEEP], 
          initializer=tf.truncated_normal_initializer(stddev=0.1)) 
      conv2_biases = tf.get_variable(
          "bias", [CONV2_DEEP], 
          initializer=tf. constant_initializer(0.0))  
 
      # 使用边长为 5，深度为 64 的过滤器，过滤器移动的步长为 1，且使用全 0 填充。   
      conv2 = tf.nn.conv2d(
          pool1, conv2_weights, strides=[1, 1, 1, 1], padding='SAME')
      relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))
   
  # 实现第四层池化层的前向传播过程。这一层和第二层的结构是一样的。这一层的输入为
  # 14×14×64 的矩阵，输出为 7×7×64 的矩阵。
  with tf.name_scope('layer4-pool2'):
      pool2 = tf.nn.max_pool(
          relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
       
  # 将第四层池化层的输出转化为第五层全连接层的输入格式。第四层的输出为 7×7×64 的矩阵，
  # 然而第五层全连接层需要的输入格式为向量，所以在这里需要将这个 7×7×64 的矩阵拉直成一
  # 个向量。pool2.get_shape 函数可以得到第四层输出矩阵的维度而不需要手工计算。注意
  # 因为每一层神经网络的输入输出都为一个 batch 的矩阵，所以这里得到的维度也包含了一个 
  # batch 中数据的个数。
  pool_shape = pool2.get_shape().as_list()
 
  # 计算将矩阵拉直成向量之后的长度，这个长度就是矩阵长宽及深度的乘积。注意这里
  # pool_shape[0] 为一个 batch 中数据的个数。
  nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
 
  # 通过 tf.reshape 函数将第四层的输出变成一个 batch 的向量。
  reshaped = tf.reshape(pool2, [pool_shape[0], nodes])
 
  # 声明第五层全连接层的变量并实现前向传播过程。这一层的输入是拉直之后的一组向量，
  # 向量长度为 3136，输出是一组长度为 512 的向量。这一层和之前在第五章中介绍的基本
  # 一致，唯一的区别就是引入了 dropout 的概念。dropout 在训练时会随机将部分节点的
  # 输出改为 0。dropout 可以避免过拟合问题，从而使得模型在测试数据上的效果更好。
  # dropout 一般只在全连接层而不是卷积层或者池化层使用。
  with tf.variable_scope('layer5-fc1'):
      fc1_weights = tf.get_variable(
          "weight", [nodes, FC_SIZE], 
           initializer=tf.truncated_normal_initializer(stddev=0.1))  
      # 只有全连接层的权重需要加入正则化。
      if regularizer != None: 
          tf.add_to_collection('losses', regularizer(fc1_weights))
      fc1_biases = tf.get_variable(
          "bias", [FC_SIZE], initializer=tf.constant_initializer(0.1))
       
      fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_biases)
      if train: fc1 = tf.nn.dropout(fc1, 0.5)
 
  # 声明第六层全连接层的变量并实现前向传播过程。这一层的输入为一组长度为 512 的向量，
  # 输出为一组长度为 10 的向量。这一层的输出通过 Softmax 之后就得到了最后的分类结果。
  with tf.variable_scope('layer6-fc2'):
      fc2_weights = tf.get_variable(
          "weight", [FC_SIZE, NUM_LABELS], 
      initializer=tf.truncated_normal_initializer(stddev=0.1)) 
      if regularizer != None: 
          tf.add_to_collection('losses', regularizer (fc2_weights))
      fc2_biases = tf.get_variable(
          "bias", [NUM_LABELS], 
          initializer=tf. constant_initializer(0.1))
     logit = tf.matmul(fc1, fc2_weights) + fc2_biases
   
  # 返回第六层的输出。
  return logit

运行修改后的 mnist_train.py 和 mnist_eval.py，可以得到一下测试结果：

 
~/mnist$ python mnist_train.py 
Extracting /tmp/data/train-images-idx3-ubyte.gz
Extracting /tmp/data/train-labels-idx1-ubyte.gz
Extracting /tmp/data/t10k-images-idx3-ubyte.gz
Extracting /tmp/data/t10k-labels-idx1-ubyte.gz
After 1 training step(s), loss on training batch is 6.45373.
After 1001 training step(s), loss on training batch is 0.824825.
After 2001 training step(s), loss on training batch is 0.646993.
After 3001 training step(s), loss on training batch is 0.759975.
After 4001 training step(s), loss on training batch is 0.68468.
After 5001 training step(s), loss on training batch is 0.630368.

上面的程序可以将 MNIST 正确率达到~99.4%。

本文内容来自作者图书作品《TensorFlow: 实战 Google 深度学习框架》，点击购买。

作者介绍

郑泽宇，才云首席大数据科学家，前谷歌高级工程师。从 2013 年加入谷歌至今，郑泽宇作为主要技术人员参与并领导了多个大数据项目，拥有丰富机器学习、数据挖掘工业界及科研项目经验。2014 年，他提出产品聚类项目用于衔接谷歌购物和谷歌知识图谱（Knowledge Graph）数据，使得知识卡片形式的广告逐步取代传统的产品列表广告，开启了谷歌购物广告在搜索页面投递的新纪元。他于 2013 年 5 月获得美国 Carnegie Mellon University（CMU）大学计算机硕士学位, 期间在顶级国际学术会议上发表数篇学术论文，并获得西贝尔奖学金。