深入浅出 TensorFlow（二）：TensorFlow 解决 MNIST 问题入门

2017 年 2 月 16 日，Google 正式对外发布 Google TensorFlow 1.0 版本，并保证本次的发布版本 API 接口完全满足生产环境稳定性要求。这是 TensorFlow 的一个重要里程碑，标志着它可以正式在生产环境放心使用。在国内，从 InfoQ 的判断来看，TensorFlow 仍处于创新传播曲线的创新者使用阶段，大部分人对于 TensorFlow 还缺乏了解，社区也缺少帮助落地和使用的中文资料。InfoQ 期望通过深入浅出 TensorFlow 系列文章能够推动 Tensorflow 在国内的发展。欢迎加入 QQ 群（群号：183248479）深入讨论和交流。

本文是整个系列的第二篇文章，将会简单介绍 TensorFlow 安装方法、TensorFlow 基本概念、神经网络基本模型，并在 MNIST 数据集上使用 TensorFlow 实现一个简单的神经网络。

TensorFlow 安装

Docker 是新一代的虚拟化技术，它可以将 TensorFlow 以及 TensorFlow 的所有依赖关系统一封装到 Docker 镜像当中，从而大大简化了安装过程。Docker 是可移植性最强的一种安装方式，它支持大部分的操作系统（比如 Windows，Linux 和 Mac OS）。对于 TensorFlow 发布的每一个版本，谷歌都提供了官方镜像。在官方镜像的基础上，才云科技提供的镜像进一步整合了其他机器学习工具包以及 TensorFlow 可视化工具 TensorBoard，使用起来可以更加方便。目前才云科技提供的镜像有：

 
cargo.caicloud.io/tensorflow/tensorflow:0.12.0 cargo.caicloud.io/tensorflow/tensorflow:0.12.0-gpu cargo.caicloud.io/tensorflow/tensorflow:0.12.1 cargo.caicloud.io/tensorflow/tensorflow:0.12.1-gpu cargo.caicloud.io/tensorflow/tensorflow:1.0.0
cargo.caicloud.io/tensorflow/tensorflow:1.0.0-gpu

当 Docker 安装完成之后（Docker 安装可以参考 https://docs.docker.com/engine/installation/），可以通过以下命令来启动一个 TensorFlow 容器。在第一次运行的时候，Docker 会自动下载镜像。

 
$ docker run -p 8888:8888 –p 6006:6006 \
   cargo.caicloud.io/tensorflow/tensorflow:1.0.0

在这个命令中，-p 8888:8888 将容器内运行的 Jupyter 服务映射到本地机器，这样在浏览器中打开 localhost:8888 就能看到 Jupyter 界面。在此镜像中运行的 Jupyter 是一个网页版的代码编辑器，它支持创建、上传、修改和运行 Python 程序。

-p 6006:6006 将容器内运行的 TensorFlow 可视化工具 TensorBoard 映射到本地机器，通过在浏览器中打开 localhost:6006 就可以将 TensorFlow 在训练时的状态、图片数据以及神经网络结构等信息全部展示出来。此镜像会将所有输出到 /log 目录底下的日志全部可视化。

-it 将提供一个 Ubuntu 14.04 的 bash 环境，在此环境中已经将 TensorFlow 和一些常用的机器学习相关的工具包（比如 Scikit）安装完毕。注意这里无论本地机器操作系统是什么，这个 bash 环境都是基于 Ubuntu 14.04 的。这是由编译 Docker 镜像的方式决定的，和本地的操作系统没有关系。

虽然有支持 GPU 的 Docker 镜像，但是要运行这些镜像需要安装最新的 NVidia 驱动以及 nvidia-docker。在安装完成 nvidia-docker 之后，可以通过以下的命令运行支持 GPU 的 TensorFlow 镜像。在镜像启动之后可以通过和上面类似的方式使用 TensorFlow。

 
$ nvidia-docker run -it -p 8888:8888 –p 6006:6006 \
cargo.caicloud.io/tensorflow/tensorflow:1.0.0-gpu

除了 Docker 安装，在本地使用最方便的 TensorFlow 安装方式是 pip。通过以下命令可以在 Linux 环境下使用 pip 安装 TensorFlow 1.0.0。

 
$ sudo apt-get install python-pip python-dev  # 安装 pip 和 Python 2.7
$ sudo pip install tensorflow                    # 安装只支持 CPU 的 TensorFlow
$ sudo pip install tensorflow-gpu               # 安装支持 GPU 的 TensorFlow

目前只有在安装了 CUDA toolkit 8.0 和 CuDNN v5.1 的 64 位 Ubuntu 下可以通过 pip 安装支持 GPU 的 TensorFlow，对于其他系统或者其他 CUDA/CuDNN 版本的用户则需要从源码进行安装来支持 GPU 使用。从源码安装 TensorFlow 可以参考 https://www.tensorflow.org/install/。

TensorFlow 样例

TensorFlow 对 Python 语言的支持是最全面的，所以本文中将使用 Python 来编写 TensorFlow 程序。下面的程序给出一个简单的 TensorFlow 样例程序来实现两个向量求和。

 
import tensorflow as tf
a = tf.constant([1.0, 2.0], name="a")
b = tf.constant([2.0, 3.0], name="b")
result = a + b
print result        # 输出“Tensor("add:0", shape=(2,), dtype=float32) ”
 
sess = tf.Session()
print sess.run(result)    # 输出“[ 3.  5.]”
sess.close()

TensorFlow 基本概念

TensorFlow 的名字中已经说明了它最重要的两个概念——Tensor 和 Flow。Tensor 就是张量。在 TensorFlow 中，所有的数据都通过张量的形式来表示。从功能的角度上看，张量可以被简单理解为多维数组。但张量在 TensorFlow 中的实现并不是直接采用数组的形式，它只是对 TensorFlow 中运算结果的引用。在张量中并没有真正保存数字，它保存的是如何得到这些数字的计算过程。在上面给出的测试样例程序中，第一个 print 输出的只是一个引用而不是计算结果。

一个张量中主要保存了三个属性：名字（name）、维度（shape）和类型（type）。张量的第一个属性名字不仅是一个张量的唯一标识符，它同样也给出了这个张量是如何计算出来的。张量的命名是通过“node:src_output”的形式来给出。其中 node 为计算节点的名称，src_output 表示当前张量来自节点的第几个输出。

比如张量“add:0”就说明了 result 这个张量是计算节点“add”输出的第一个结果（编号从 0 开始）。张量的第二个属性是张量的维度（shape）。这个属性描述了一个张量的维度信息。比如“shape=(2,) ”说明了张量 result 是一个一维数组，这个数组的长度为 2。张量的第三个属性是类型（type），每一个张量会有一个唯一的类型。TensorFlow 会对参与运算的所有张量进行类型的检查，当发现类型不匹配时会报错。

如果说 TensorFlow 的第一个词 Tensor 表明了它的数据结构，那么 Flow 则体现了它的计算模型。Flow 翻译成中文就是“流”，它直观地表达了张量之间通过计算相互转化的过程。

TensorFlow 是一个通过计算图的形式来表述计算的编程系统。TensorFlow 中的每一个计算都是计算图上的一个节点，而节点之间的边描述了计算之间的依赖关系。图 1 展示了通过 TensorBoard 画出来的测试样例的计算图。

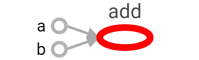
图 1 通过 TensorBoard 可视化测试样例的计算图

图 1 中的每一个节点都是一个运算，而每一条边代表了计算之间的依赖关系。如果一个运算的输入依赖于另一个运算的输出，那么这两个运算有依赖关系。在图 1 中，a 和 b 这两个常量不依赖任何其他计算。而 add 计算则依赖读取两个常量的取值。于是在图 1 中可以看到有一条从 a 到 add 的边和一条从 b 到 add 的边。在图 1 中，没有任何计算依赖 add 的结果，于是代表加法的节点 add 没有任何指向其他节点的边。所有 TensorFlow 的程序都可以通过类似图 1 所示的计算图的形式来表示，这就是 TensorFlow 的基本计算模型。

TensorFlow 计算图定义完成后，我们需要通过会话（Session）来执行定义好的运算。会话拥有并管理 TensorFlow 程序运行时的所有资源。当所有计算完成之后需要关闭会话来帮助系统回收资源，否则就可能出现资源泄漏的问题。TensorFlow 可以通过 Python 的上下文管理器来使用会话。以下代码展示了如何使用这种模式。

 
# 创建一个会话，并通过 Python 中的上下文管理器来管理这个会话。
with tf.Session() as sess
# 使用这创建好的会话来计算关心的结果。
sess.run(...)
# 不需要再调用“Session.close()”函数来关闭会话，
# 当上下文退出时会话关闭和资源释放也自动完成了。

通过 Python 上下文管理器的机制，只要将所有的计算放在“with”的内部就可以。当上下文管理器退出时候会自动释放所有资源。这样既解决了因为异常退出时资源释放的问题，同时也解决了忘记调用 Session.close 函数而产生的资源泄。

TensorFlow 实现前向传播

为了介绍神经网络的前向传播算法，需要先了解神经元的结构。神经元是构成一个神经网络的最小单元，图 2 显示了一个神经元的结构。

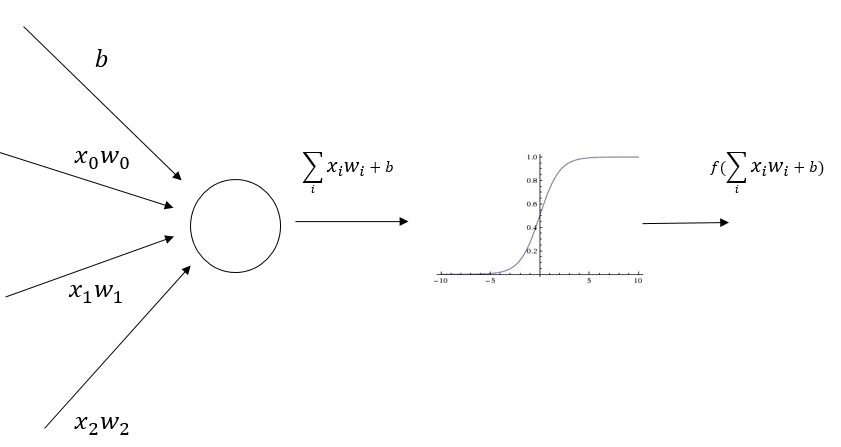
图 2 神经元结构示意图

从图 2 可以看出，一个神经元有多个输入和一个输出。每个神经元的输入既可以是其他神经元的输出，也可以是整个神经网络的输入。所谓神经网络的结构就是指的不同神经元之间的连接结构。如图 2 所示，神经元结构的输出是所有输入的加权和加上偏置项再经过一个激活函数。图 3 给出了一个简单的三层全连接神经网络。之所以称之为全连接神经网络是因为相邻两层之间任意两个节点之间都有连接。这也是为了将这样的网络结构和后面文章中将要介绍的卷积层、LSTM 结构区分。图 3 中除了输入层之外的所有节点都代表了一个神经元的结构。本小节将通过这个样例来解释前向传播的整个过程。

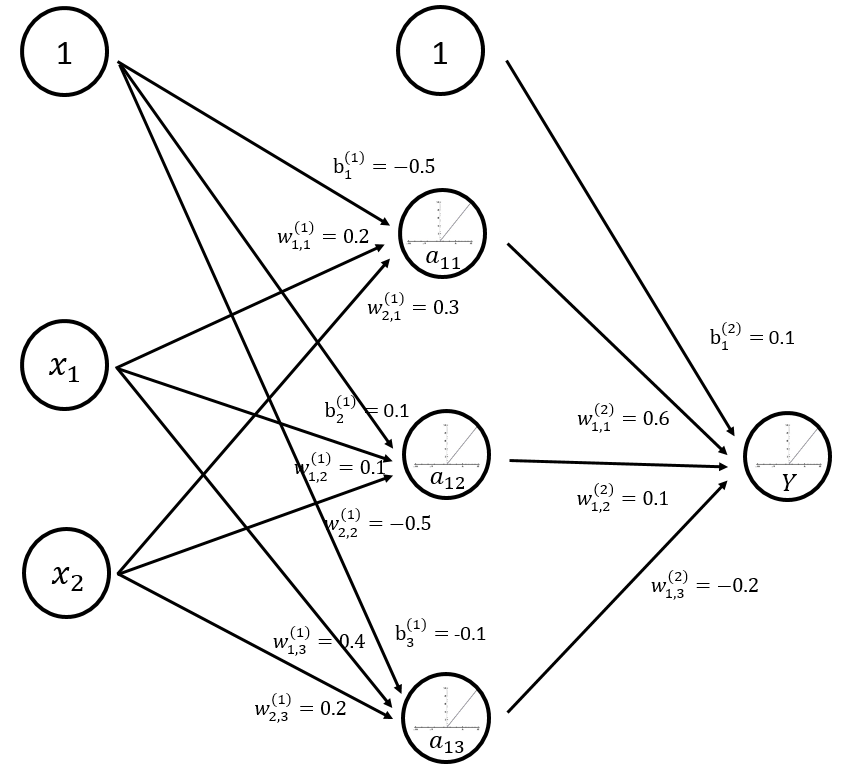
图 3 三层全连接神经网络结构图

计算神经网络的前向传播结果需要三部分信息。第一个部分是神经网络的输入，这个输入就是从实体中提取的特征向量。第二个部分为神经网络的连接结构。神经网络是由神经元构成的，神经网络的结构给出不同神经元之间输入输出的连接关系。神经网络中的神经元也可以称之为节点。在图 3 中，a11 节点有两个输入，他们分别是 x1 和 x2 的输出。而 a11 的输出则是节点 Y 的输入。最后一个部分是每个神经元中的参数。图 3 用 w 来表示神经元中的权重，b 表示偏置项。W 的上标表明了神经网络的层数，比如 W(1) 表示第一层节点的参数，而 W(2) 表示第二层节点的参数。W 的下标表明了连接节点编号，比如 W1,2(1) 表示连接 x1 和 a12 节点的边上的权重。给定神经网络的输入、神经网络的结构以及边上权重，就可以通过前向传播算法来计算出神经网络的输出。下面公式给出了在 ReLU 激活函数下图 3 神经网络前向传播的过程。

 
a11=f(W1,1(1)x1+W2,1(1)x2+b1(1))=f(0.7×0.2+0.9×0.3+(-0.5))=f(-0.09)=0
a12=f(W1,2(1)x1+W2,2(1)x2+b2(1))=f(0.7×0.1+0.9×(-0.5)+0.1)=f(-0.28)=0
a13=f(W1,3(1)x1+W2,3(1)x2+b3(1))=f(0.7×0.4+0.9×0.2+(-0.1))=f(0.36)=0.36
Y=f(W1,1(2)a11+W1,2(2)a12+W1,3(2)a13+b1(2))=f(0.054+0.028+(-0.072)+0.1)=f(0.11)=0.11

在 TensorFlow 中可以通过矩阵乘法的方法实现神经网络的前向传播过程。

 
a = tf.nn.relu(tf.matmul(x, w1)+b1)
y = tf.nn.relu(tf.matmul(a, w2)+b2)

在上面的代码中并没有定义 w1、w2、b1、b2，TensorFlow 可以通过变量（tf.Variable）来保存和更新神经网络中的参数。比如通过下面语句可以定义 w1：

 
weights = tf.Variable(tf.random_normal([2, 3], stddev=2))

这段代码调用了 TensorFlow 变量的声明函数 tf.Variable。在变量声明函数中给出了初始化这个变量的方法。TensorFlow 中变量的初始值可以设置成随机数、常数或者是通过其他变量的初始值计算得到。在上面的样例中，tf.random_normal([2, 3], stddev=2) 会产生一个 2×3 的矩阵，矩阵中的元素是均值为 0，标准差为 2 的随机数。tf.random_normal 函数可以通过参数 mean 来指定平均值，在没有指定时默认为 0。通过满足正太分布的随机数来初始化神经网络中的参数是一个非常常用的方法。下面的样例介绍了如何通过变量实现神经网络的参数并实现前向传播的过程。

 
import tensorflow as tf
 
# 声明变量。
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
b1 = tf.Variable(tf.constant(0.0, shape=[3]))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
b2 = tf.Variable(tf.constant(0.0, shape=[1]))
 
# 暂时将输入的特征向量定义为一个常量。注意这里 x 是一个 1*2 的矩阵。
x = tf.constant([[0.7, 0.9]])  
 
# 实现神经网络的前向传播过程，并计算神经网络的输出。
a = tf.nn.relu(tf.matmul(x, w1)+b1)
y = tf.nn.relu(tf.matmul(a, w2)+b2)
 
sess = tf.Session()
# 运行变量初始化过程。
init_op = tf.global_variables_initializer()
sess.run(init_op)
# 输出 [[3.95757794]]
print(sess.run(y))  
sess.close()

TensorFlow 实现反向传播

在前向传播的样例程序中，所有变量的取值都是随机的。在使用神经网络解决实际的分类或者回归问题时需要更好地设置参数取值。使用监督学习的方式设置神经网络参数需要有一个标注好的训练数据集。以判断零件是否合格为例，这个标注好的训练数据集就是收集的一批合格零件和一批不合格零件。监督学习最重要的思想就是，在已知答案的标注数据集上，模型给出的预测结果要尽量接近真实的答案。通过调整神经网络中的参数对训练数据进行拟合，可以使得模型对未知的样本提供预测的能力。

在神经网络优化算法中，最常用的方法是反向传播算法（backpropagation）。图 4 展示了使用反向传播算法训练神经网络的流程图。本文将不过多讲解反向传播的数学公式，而是重点介绍如何通过 TensorFlow 实现反向传播的过程。

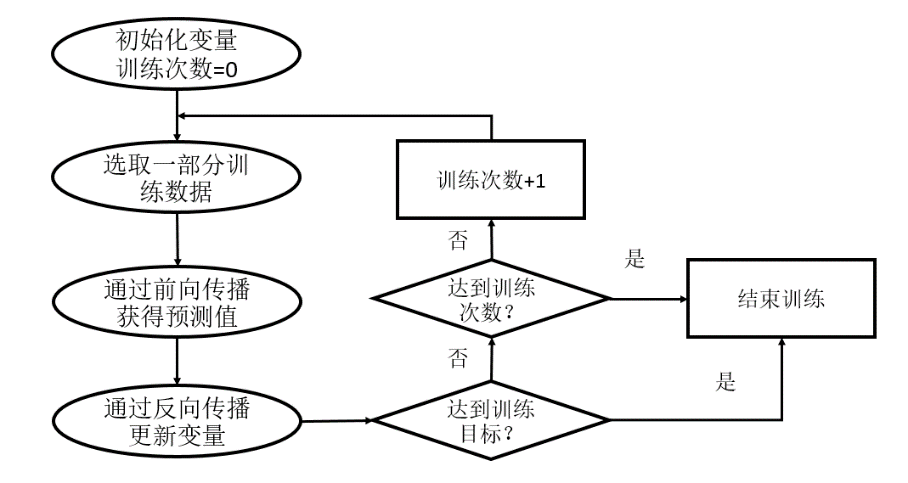
图 4 使用反向传播优化神经网络的流程图

从图 4 中可以看出，通过反向传播算法优化神经网络是一个迭代的过程。在每次迭代的开始，首先需要选取一小部分训练数据，这一小部分数据叫做一个 batch。然后，这个 batch 的样例会通过前向传播算法得到神经网络模型的预测结果。因为训练数据都是有正确答案标注的，所以可以计算出当前神经网络模型的预测答案与正确答案之间的差距。最后，基于这预测值和真实值之间的差距，反向传播算法会相应更新神经网络参数的取值，使得在这个 batch 上神经网络模型的预测结果和真实答案更加接近。通过 TensorFlow 实现反向传播算法的第一步是使用 TensorFlow 表达一个 batch 的数据。在上面的样例中使用了常量来表达过一个样例：

 
x = tf.constant([[0.7, 0.9]])  

但如果每轮迭代中选取的数据都要通过常量来表示，那么 TensorFlow 的计算图将会太大。因为每生成一个常量，TensorFlow 都会在计算图中增加一个节点。一般来说，一个神经网络的训练过程会需要经过几百万轮甚至几亿轮的迭代，这样计算图就会非常大，而且利用率很低。为了避免这个问题，TensorFlow 提供了 placeholder 机制用于提供输入数据。placeholder 相当于定义了一个位置，这个位置中的数据在程序运行时再指定。这样在程序中就不需要生成大量常量来提供输入数据，而只需要将数据通过 placeholder 传入 TensorFlow 计算图。在 placeholder 定义时，这个位置上的数据类型是需要指定的。和其他张量一样，placeholder 的类型也是不可以改变的。placeholder 中数据的维度信息可以根据提供的数据推导得出，所以不一定要给出。下面给出了通过 placeholder 实现前向传播算法的代码。

 
x = tf.placeholder(tf.float32, shape=(1, 2), name="input")
# 其他部分定义和上面的样例一样。
print(sess.run(y, feed_dict={x: [[0.7,0.9]]}))  

在调用 sess.run 时，我们需要使用 feed_dict 来设定 x 的取值。在得到一个 batch 的前向传播结果之后，需要定义一个损失函数来刻画当前的预测值和真实答案之间的差距。然后通过反向传播算法来调整神经网络参数的取值使得差距可以被缩小。损失函数将在后面的文章中更加详细地介绍。以下代码定义了一个简单的损失函数，并通过 TensorFlow 定义了反向传播的算法。

 
# 定义损失函数来刻画预测值与真实值得差距。
cross_entropy = -tf.reduce_mean(
   y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) 
# 定义学习率。
learning_rate = 0.001
# 定义反向传播算法来优化神经网络中的参数。
train_step = 
   tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)

在上面的代码中，cross_entropy 定义了真实值和预测值之间的交叉熵（cross entropy），这是分类问题中一个常用的损失函数。第二行 train_step 定义了反向传播的优化方法。目前 TensorFlow 支持 10 种不同的优化器，读者可以根据具体的应用选择不同的优化算法。比较常用的优化方法有三种：tf.train.GradientDescentOptimizer、class tf.train.AdamOptimizer 和 tf.train.MomentumOptimizer。

TensorFlow 解决 MNIST 问题

MNIST 是一个非常有名的手写体数字识别数据集，在很多资料中，这个数据集都会被用作深度学习的入门样例。MNIST 数据集是 NIST 数据集的一个子集，它包含了 60000 张图片作为训练数据，10000 张图片作为测试数据。在 MNIST 数据集中的每一张图片都代表了 0-9 中的一个数字。图片的大小都为 28×28，且数字都会出现在图片的正中间。图 5 展示了一张数字图片及和它对应的像素矩阵：

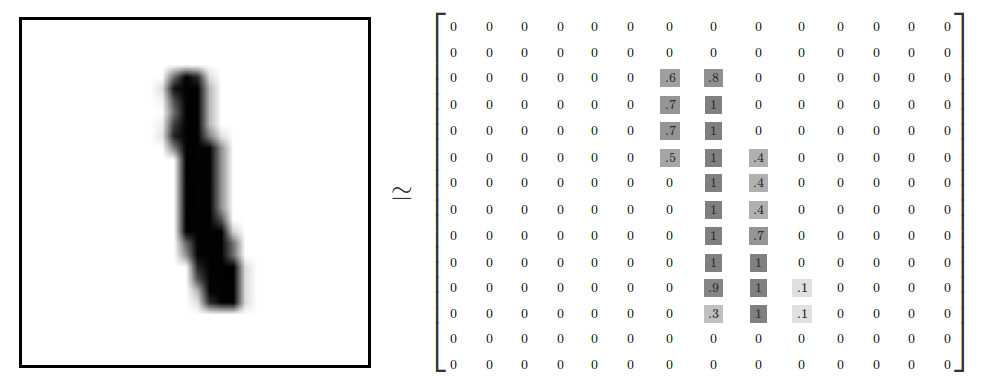
图 5. MNIST 数字图片及其像素矩阵。

在图 5 的左侧显示了一张数字 1 的图片，而右侧显示了这个图片所对应的像素矩阵。MNIST 数据集中图片的像素矩阵大小为 28×28，但为了更清楚的展示，图 5 右侧显示的为 14×14 的矩阵。在 Yann LeCun 教授的网站中（ http://yann.lecun.com/exdb/mnist）对 MNIST 数据集做出了详细的介绍。TensorFlow 对 MNIST 数据集做了更高层的封装，使得使用起来更加方便。下面给出了样例 TensorFlow 代码来解决 MNIST 数字手写体分类问题。

 
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
 
# MNIST 数据集相关的常数。
INPUT_NODE = 784      # 输入层的节点数。对于 MNIST 数据集，这个就等于图片的像素。   
OUTPUT_NODE = 10     # 输出层的节点数。这个等于类别的数目。因为在 MNIST 数据集中
                        # 需要区分的是 0~9 这 10 个数字，所以这里输出层的节点数为 10。
 
# 配置神经网络的参数。
LAYER1_NODE = 500   # 隐藏层节点数。这里使用只有一个隐藏层的网络结构作为样例。
                       # 这个隐藏层有 500 个节点。
BATCH_SIZE = 100    # 一个训练 batch 中的训练数据个数。数字越小时，训练过程越接近
                       # 随机梯度下降；数字越大时，训练越接近梯度下降。
LEARNING_RATE = 0.01           # 学习率。
TRAINING_STEPS = 10000              # 训练轮数。
 
# 训练模型的过程。
def train(mnist):
   x = tf.placeholder(tf.float32, [None, INPUT_NODE], name='x-input')
   y_ = tf.placeholder(tf.float32, [None, OUTPUT_NODE], name='y-input')
   
   # 定义神经网络参数。
weights1 = tf.Variable(
   tf.truncated_normal([INPUT_NODE, LAYER1_NODE], stddev=0.1))
bias1 = tf.Variable(tf.constant(0.0, shape=[LAYER1_NODE]))
weights2 = tf.Variable(
   tf.truncated_normal([LAYER1_NODE, OUTPUT_NODE], stddev=0.1))
bias2 = tf.Variable(tf.constant(0.0, shape=[OUTPUT_NODE]))
 
# 计算在当前参数下神经网络前向传播的结果。
   layer1 = tf.nn.relu(tf.matmul(input_tensor, weights1) + bias1)
   y = tf.matmul(layer1, weights2) + bias2
 
# 定义存储训练轮数的变量。 
   global_step = tf.Variable(0, trainable=False)
   
# 计算交叉熵作为刻画预测值和真实值之间差距的损失函数。
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(
   labels=y_, logits=y)
   loss = tf.reduce_mean(cross_entropy)
          
   # 使用 tf.train.GradientDescentOptimizer 优化算法来优化损失函数。注意这里损失
   # 函数包含了交叉熵损失和 L2 正则化损失。
   train_op=tf.train.GradientDescentOptimizer(LEARNING_RATE)\
                .minimize(loss, global_step=global_step)
 
   # 检验神经网络的正确率。
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_,1))
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
 
   # 初始化会话并开始训练过程。
   with tf.Session() as sess:
   tf.initialize_all_variables().run()
   # 准备验证数据。一般在神经网络的训练过程中会通过验证数据来大致判断停止的
   # 条件和评判训练的效果。
       validate_feed = {x: mnist.validation.images, 
                            y_: mnist.validation.labels}
 
   # 准备测试数据。在真实的应用中，这部分数据在训练时是不可见的，这个数据只是作为  
   # 模型优劣的最后评价标准。
       test_feed = {x: mnist.test.images, y_: mnist.test.labels}     
 
       # 迭代地训练神经网络。
       for i in range(TRAINING_STEPS):
           # 每 1000 轮输出一次在验证数据集上的测试结果。
           if i % 1000 == 0:
   validate_acc = sess.run(accuracy, feed_dict=validate_feed)
                 print("After %d training step(s), validation accuracy "
                        "using average model is %g " % (i, validate_acc))
           
           # 产生这一轮使用的一个 batch 的训练数据，并运行训练过程。
           xs, ys = mnist.train.next_batch(BATCH_SIZE)
           sess.run(train_op, feed_dict={x: xs, y_: ys})
 
       # 在训练结束之后，在测试数据上检测神经网络模型的最终正确率。
       test_acc = sess.run(accuracy, feed_dict=test_feed)
   print("After %d training step(s), test accuracy using average "
          "model is %g" % (TRAINING_STEPS, test_acc))
 
# 主程序入口
def main(argv=None): 
   # 声明处理 MNIST 数据集的类，这个类在初始化时会自动下载数据。
   mnist = input_data.read_data_sets("/tmp/data", one_hot=True)
   train(mnist)
 
# TensorFlow 提供的一个主程序入口，tf.app.run 会调用上面定义的 main 函数。
if __name__ == '__main__':
tf.app.run()

运行上面代码可以得到结果：

 
After 0 training step(s), validation accuracy using average model is 0.103 
After 1000 training step(s), validation accuracy using average model is 0.9044 
After 2000 training step(s), validation accuracy using average model is 0.9174 
After 3000 training step(s), validation accuracy using average model is 0.9258 
After 4000 training step(s), validation accuracy using average model is 0.93 
After 5000 training step(s), validation accuracy using average model is 0.9346 
After 6000 training step(s), validation accuracy using average model is 0.94 
After 7000 training step(s), validation accuracy using average model is 0.9422 
After 8000 training step(s), validation accuracy using average model is 0.9472 
After 9000 training step(s), validation accuracy using average model is 0.9498 
After 10000 training step(s), test accuracy using average model is 0.9475

通过该程序可以将 MNIST 数据集的准确率达到~95%。