敲开图灵之门：量子计算与机器学习

本文最初发表于 The Gradient ，经原作者 Ather Fawaz 授权，由 InfoQ 中文站翻译并分享。

零和一。零零碎碎。阴与阳。最重要的是，开关，有些是开，有些是关。人们已经习惯于看到和使用现代计算机。每年，像英特尔、AMD、ARM 和英伟达这样的行业巨擘，都会发布他们的下一代顶级芯片，不断地互相竞争，并将其推向极限。

当我们仔细评估这些新的多核 CPU、 GPU 和云端托管的大型计算集群时，我们很快意识到更快的处理器不一定能提高计算能力。

的确，计算速度在过去的几十年中呈指数级增长，但是我们能够处理的数据量也在增长。我们可以在互联网上存储和分析艾字节（译注：艾字节：ExaByte，EB，一种信息计量单位，现今通常在标示网络硬盘总容量，或具有大容量的保存媒介之保存容量时使用。1EB=1024PB==2⁶⁰字节）数据，用来训练像OpenAI 的 GPT-3这样的深度学习模型，以及实现在围棋和国际象棋等复杂游戏中击败冠军和特级大师所需的计算能力。

但是，所有这些技术进步是否已经从根本上扩大了我们能用计算机做的事情，超出了我们最初使用计算机的范围呢？或者简单地说，我们是否改变了我们经典的计算模式？

现代计算机是按照冯·诺依曼结构（von Neumann architecture）的原理运行的（Ogban 等人，2007 年）。冯·诺依曼结构利用输入和输出到处理器的逻辑函数，根据一组指令对输入进行操作。

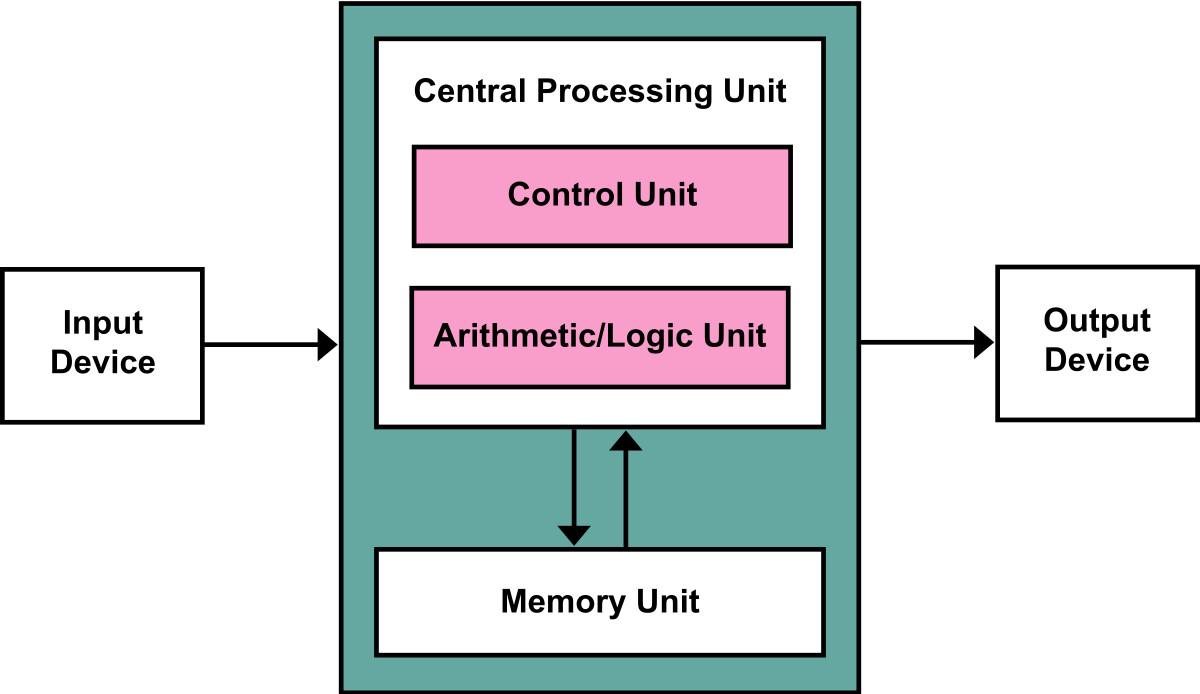
冯·诺依曼结构

尽管冯·诺依曼结构有助于实际解决问题，但是它们并不能描述计算过程本身。为此，我们需要图灵机（De Mol 等人，2018 年）。图灵机提供了当今计算机的抽象模型。图灵机按一套规则操纵磁带上的符号。接着磁带会根据机器的当前状态继续或停止。

众所周知，经典计算机现在能够进行的所有计算，都可以在图灵机上完成。精明的读者会将这一结果与丘奇 - 图灵论题（Church-Turing thesis）联系起来，后者指出，“任何现实世界的计算都可以通过 λ 演算（λ-calculus）来完成，这相当于使用一般递归函数”（Rabin，2012 年）。然而，在实践中，对于任何实际的、合理大小的问题来说，图灵机实际上都太慢了。

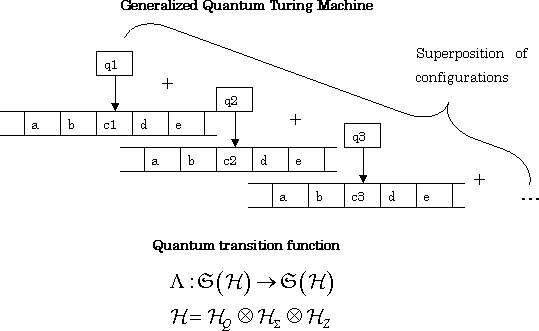
图灵机的图解表示

正如丘奇 - 图灵论题所证明的那样，图灵机提供的可计算性是我们尚未突破的玻璃天花板。正如我们稍后要讨论的那样，尽管我们的计算设备以图灵机为基础，开启了计算的可能性，但是这个模型本身也有一些固有的缺陷，令人望而却步。

但这并不意味着，一切都已经结束了。马丁·路德·金（Martin Luther King Jr.）曾说过：“我们必须接受失望，因为它是有限的，但千万不可失去希望，因为它是无穷的。”（We must accept finite disappointment, but never lose infinite hope.）要打破这一玻璃天花板，需要的不仅仅是在计算机芯片上装上大量的晶体管。它需要从根本上对计算机进行彻底的重新思考；从最基本的单元——比特开始。

进入量子领域

在过去的 120 年里，也许是物理学史上最伟大的进步。爱因斯坦的狭义相对论和广义相对论改变了我们对时间、空间和引力的认识，而狄拉克、泡利、费曼、薛定谔、海森堡和普朗克关于量子力学的公式则从根本上彻底改变了我们关于电子、质子和中子这个无穷小世界的理解。

1927 年索尔维国际会议（Solvay International Conference）被视为现代物理学的转折点

量子力学是这些进步中的最后一个，它与寻求强大的新计算模型有着最直接的联系。20 世纪 80 年代初，理查德·费曼设想，量子计算机能够提供一种解决当代（或经典）计算机难以指数化解决的问题的方法（费曼，1986 年）。量子计算机要求我们采用一个完全不同的比特概念，这是有可能的。在深入研究这种计算模式之前，我们首先必须定义量子计算机的含义。

与经典计算机不同的是，经典计算机的比特在任何时刻都可以存在于 0 或 1 的状态，而量子计算机中的量子比特（或简称量子位，qubit）可以存在于额外的状态。它可以作为离散状态（0 或 1）存在，也可以作为两种状态的叠加存在。这是量子比特的一个固有属性，它为其定域性赋予了一个概率分布。

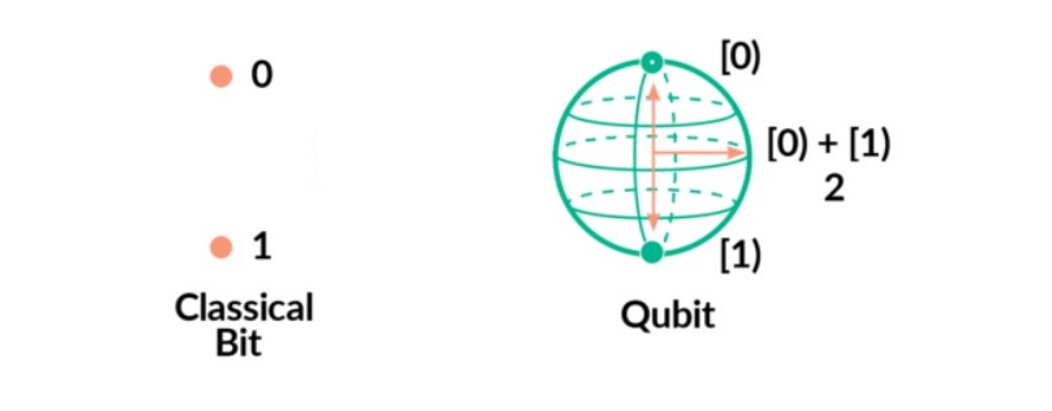
经典比特与量子比特

本文目的不是解释量子计算机背后的量子偏心。然而，有必要回顾量子物理学的两个基本概念：波粒二象性和纠缠。我们在后面将会看到，正是这两个概念构成了量子计算机的基石。

量子力学插曲

量子比特的状态可以表示为列向量。不同的状态由不同的列向量表示，其中每个列向量与其余列向量正交。一个量子比特对应的状态是由可能的状态的线性组合给出的，这些可能的状态用复数加权。这相当于说，在任何给定的时刻，量子比特处于这些基态的叠加，或者说处于概率波中。测量所有这些可能位置中某一精确位置的行为将导致这种概率波，或波函数塌缩，从而揭示出单一状态。

这就是波粒二象性的关键之处：一个粒子既表现出类似波的行为，又表现出类似粒子的行为。在我们明确地观察到一个粒子之前，我们永远无法说出它处于什么状态；哥本哈根解释正式提出了一个关于测量前粒子位置的问题（Faye，2002 年）。

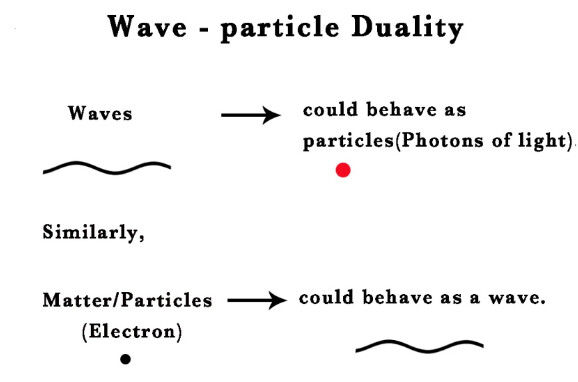
波粒二象性

第二个需要理解的重要原理是量子纠缠。以粒子系统为例，每个粒子都有自己的波函数。一个多粒子的系统被定义为状态空间的张量积。这个由 k 个粒子组成的张量积，每个粒子由一个 n 维的列向量表示，称为具有 nᵏ维。这种状态空间的表示方法称为状态的集合。

为了说明这一点，让我们把我们的初始系统中的 k 个粒子简化成只有两个，每个粒子都处于 a 和 b 两种状态的叠加中（为简单起见，也可以是圆形或正方形）。假如一种粒子的状态知识不能揭示另一种粒子的状态，那么我们可以说这两种粒子是独立的。

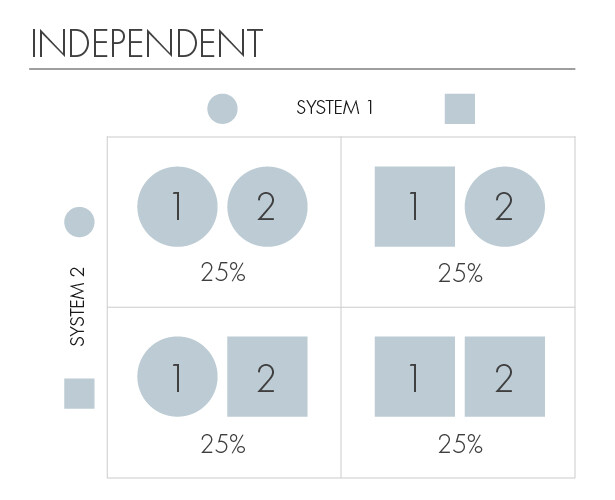
独立粒子

但是，如果知道一个粒子的状态，就能立即得到另一个粒子状态的信息，那么我们就可以说这两个粒子是纠缠的。最令人困惑的实验结果之一是：无论两个纠缠粒子之间的距离有多远，测量一个粒子的状态都能在瞬间揭示出另一个粒子的信息，而这正是我们能够迅速得到的。

这意味着如果产生两个纠缠的粒子，把它们带到太阳系的相对两端，一个粒子的波函数坍缩，另一个粒子的波函数也会立即坍缩。两个粒子之间的这种通讯速度比光速还快，因此爱因斯坦将这种奇特现象称为“鬼魅般的超距作用”（spooky action at a distance.）。

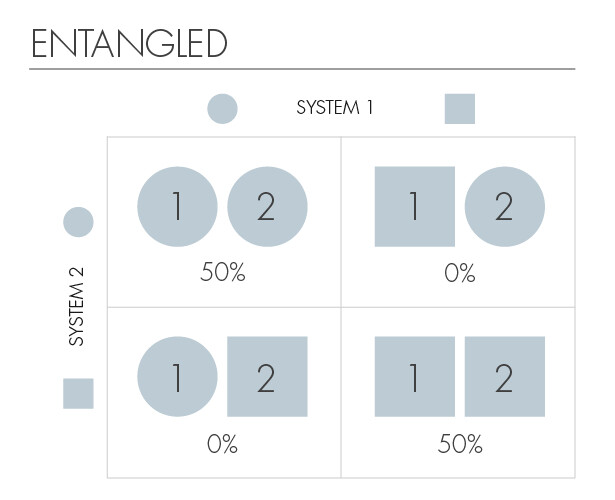
处于纠缠态的量子

沉迷于纠缠的更深指导，需要一些严格的数学公式，故本文不再赘述。此外，尽管纠缠以比光速更快的速度传输信息，但它并没有违反定域性。但有关这方面的更多细节，请参阅该指南（Wilczek，2016 年）。

在实践中，由于系统间的相互作用会导致纠缠，因此很少会遇到独立的粒子，而粒子之间的相关性是由连接波函数和具体概率的基本数学原理引入的（Joos，2009 年）。对于波粒二象性和量子纠缠的概念，让我们看看量子计算机如何巧妙地利用这些现象进行计算。

完全不同的计算模型

就像在经典计算机中晶体管代表 1 比特的信息一样，硅或磷等半导体材料的核自旋代表一个量子比特的信息。这些半导体硅或磷原子通过电场和磁场进行操纵和读取（Vogel，N.D.，Physics World 期刊，2019 年）。

如前所述，量子比特是量子计算机的基本单元。由于量子比特可以以更多的状态存在，而不仅仅是一个经典比特的 0 和 1，因此我们可以使用它们来编码更多的信息。实际上，使用量子比特编码经典比特是可能的，但反之则不然。量子比特的信息不能在经典晶体管中被编码。

对于比特，n 个晶体管可以用来编码 n 分量系统；封装一个 8 位经典系统只需要 8 个存储位。若 n 分量系统是量子的，则需要 2ⁿ 个复数来编码它（Kopczyk，2018 年）。推而广之，编码一台 8 量子比特的量子计算机需要 256 个复数。而要在经典机器上模拟 64 个量子比特，则需要 2⁶⁴=18,446,744,073,709,551,616 个复数。

因此，相对于经典计算机，量子计算提供了一个更大的势态空间；尽管量子比特是一个更大的计算对象，但它需要更少的量子比特来表示困难的计算问题。显然，经典计算机很难模仿这样的表示。

就像经典门（如 AND、OR、XOR）是对比特进行任何操作的面包和黄油一样，量子门也是通过相应的量子门来修改量子比特的状态。然而，量子计算机有一组特殊的门，这些门是特定于量子比特操作的。其中包括Hadamard 门和CNOT 门（Djordjevic，2012 年）。

Hadamard 门可用于创建状态的叠加（Qiskit/IBM，未标明日期），而 CNOT 门可以用来纠缠量子比特（Qiskit/IBM，未标明日期）。

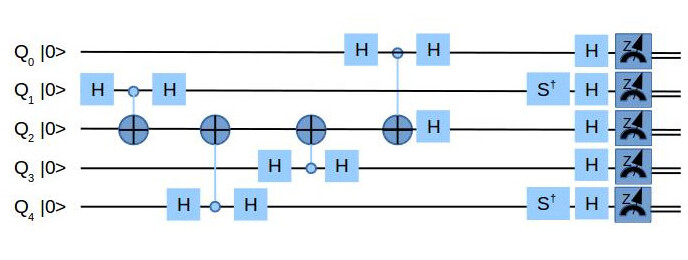
量子电路

通过使用量子门，量子计算将从接收输入的某个初始状态开始。从那里，它向最终状态过渡，然后可以对其进行测量以检索特定信息。

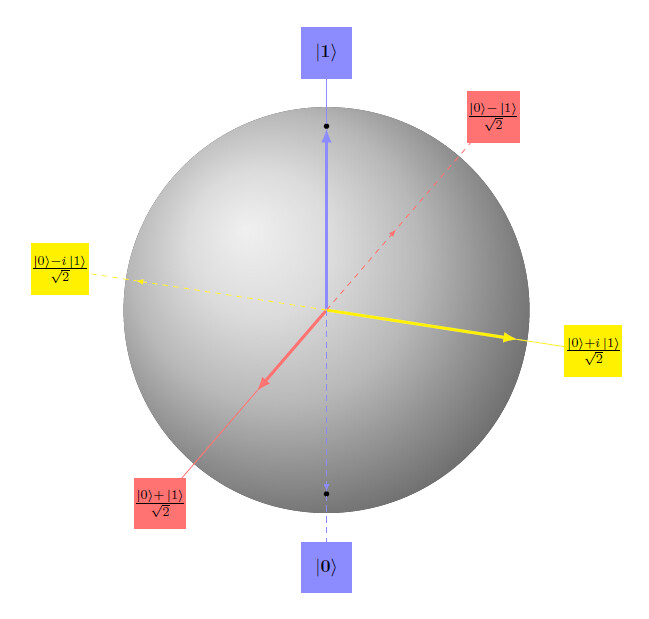
应用在量子比特上的可能变换可以用布洛赫球面（Bloch sphere）的旋转来表示

量子计算机巧妙地利用了叠加和纠缠的原理，从而能够同时计算来自多个量子比特的结果（Kopczyk，2018 年）。举例来说，假设我们的量子计算需要对一组输入进行转换或者使用函数，我们可以把这个函数应用到多个输入端，同时得到它们的结果。

相反，对于经典计算机的相同操作需要按照每个输入顺序执行，或按照单个经典电路执行。举例说明，由于经典比特没有纠缠，也没有叠加，所以要从中提取信息，需要分别测量和计算。对于量子计算机来说，纠缠和叠加使我们可以在同一时间内同时计算有关多个量子比特的信息。实质上，这个计算模型让我们可以探索不同的路径，并同时进行数学运算。

这是量子计算机的一大优点。固有的并行性相当强大，因此我们称之为“指数计算能力”。要使这种能力翻倍，我们只需在电路中再增加一个量子比特。这一发现导致了导致了量子算法的发展，量子算法利用量子计算机所提供的并行性，在某些问题的求解速度比经典最佳解快得多。

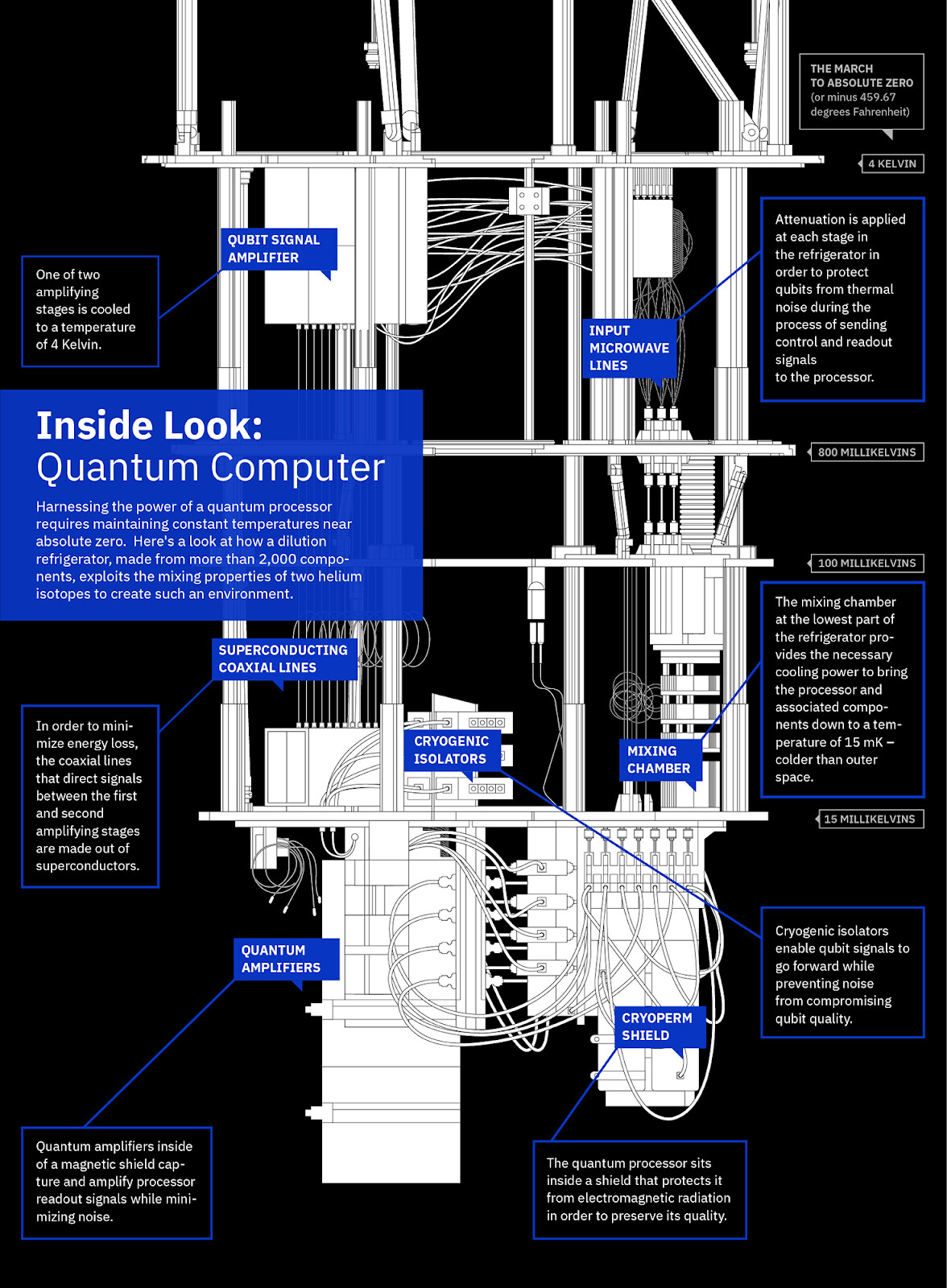
量子计算机的详细概述

在 2019 年，量子计算机超越经典计算机的首次有形展示首次亮相。谷歌的研究人员使用 53 位量子计算机 Sycamore 在 200 秒内解决了一个问题。相反，这个同样的问题，现有的一台经典超级计算机大约需要 1 万年才能解决。Sycamore 的研究结果被官方称为“量子霸权”的展示，这是一个显而易见的例子，表明量子计算范式显然比经典计算范式更为强大（Arute 与 Arya，2019 年，第 505~510 页）。

谷歌的量子计算机 Sycamore，拥有 53 位量子比特

虽然 IBM 很快用自己的后续论文（Pednault 等人，2019 年）对谷歌的说法提出了质疑，但谷歌的研究成果（《使用可编程超导处理器的量子霸权》（Quantum supremacy using a programmable superconducting processor））被普遍视为量子计算机发展的突破性时刻。

量子计算世界未非想象般美好

迄今为止，我们只讨论了量子计算机的积极方面。但是它的实现和发展并不是一帆风顺的。事实证明，在叠加状态下悬浮量子比特非常困难。

为了实现稳定性，量子计算机需要被保存在冰箱中，冰箱将量子比特要冷却到接近绝对零度（0 K）的温度。这意味着量子计算机仅限于小众研究领域和昂贵的实验室，至少现在是这样。

一个典型的 NISQ 时代的量子计算机环境

此外，量子比特容易受到噪声的影响（这种现象被称为退相干（decoherence）），这意味着它们在相互作用的粒子环境中失去了概率量子行为和存储的信息。这是因为在量子层面上，任何观察或相互作用都无法温和地从一个系统同时获取信息，但却可以保持其原始的不受干扰状态。

这种交互作用有效地将量子定域化，导致有利的状态叠加消失（Bacciagaluppi,2020 年），这也是为什么我们没能实现量子计算机的全部潜力（Kopczyk，2018 年）。

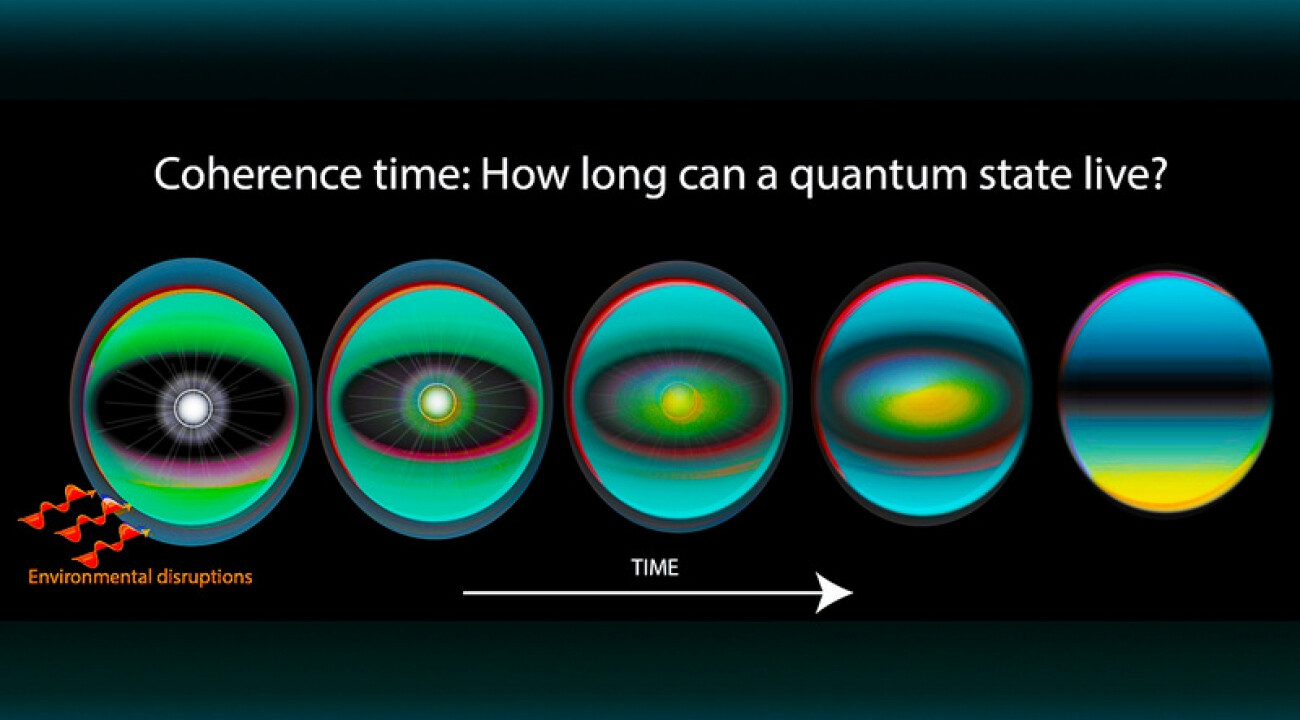
关于连贯性的问题

考虑到它们的局限性，我们正处于研究人员所说的“嘈杂中型量子”（Noisy Intermediate-Scale Quantum，NISQ）时代。现有的量子计算机的能力还不足以产生容错结果。退相干还会影响量子算法的有效性，破坏其加速优势。

同时，由于Shor 算法能够在多项式时间内对大量数据进行质因式处理，因而有可能破坏我们现有的加密标准，但它仍是一种理论上的进展。

最重要的是，量子计算机并不是每种计算类型的上乘选择。它们不会更快的完成两个数字的基本运算，也不会轻松地训练神经网络，当然也不会更快地运行日常程序。

像 IBM 这样的公司甚至声称，量子计算机“永远不会在经典计算机中占据‘霸权’地位，而是会与它们协同工作，因为每种计算机都有其独特的优势。”（Pednault 与 Gunnels，2019 年）

然而，量子计算机在某些问题上有过人之处，这是值得讨论的。

量子机器学习

近年来的研究表明，量子计算的真正潜力在于建立一个由经典段和量子段共同组成的管道。对于科学应用，我们必须计算粒子的基态。这一问题在研究化学反应和平衡时往往很重要。基态被定义为粒子处于最低能级的状态，因而也是最稳定的状态。

传统上，要获得基态，需要从粒子态的本征向量中计算出最小本征值，这些本征向量由称为哈密顿（Hamiltonian）量的矩阵来表示。对于小型系统，经典计算机在求解时并不会很费力，但对含有大量粒子的大系统来说，这一简单的任务将以指数方式增长，很快就会破坏可用的计算资源。

但是，如果我们使用混合的量子机器学习算法，这种搜索空间的增加就变得容易处理。变分量子本征求解器（Variational-Quantum-Eigensolver ，VQE）利用经典算法和量子算法来估计哈密顿量的最低本征值。

简而言之，它的量子部分叫做 ansatz，可以智能地搜索出粒子的所有可能状态的空间。经典部分通过梯度下降来调整 ansatz 参数，使其接近最优解。这一组合表明，量子计算机在这类粒子模拟任务中特别有用。

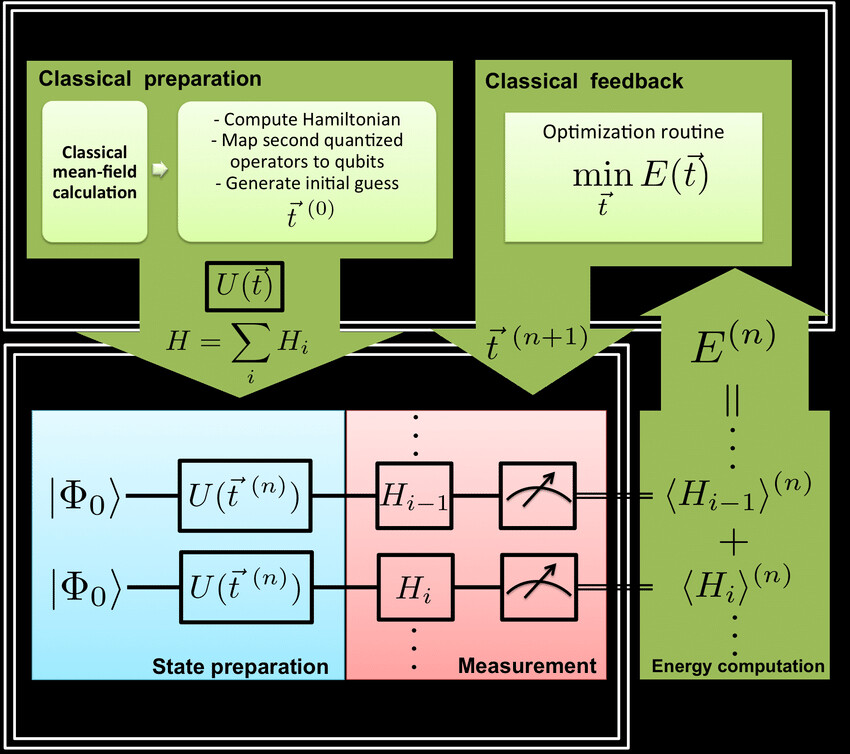
VQE 算法示意图

在过去的几年里，其他各种量子机器学习算法也得到了发展。用于经典 k- 均值聚类的最著名的量子算法优化了向量之间的 Lloyd 经典距离计算子程序（Rebollo-Monedero 与 Girod，2009 年），以将经典O(NkM)计算复杂度呈指数级地降低到O(Mklog(N))，其中k是聚类的数量，M是训练样本的数量，并且N是特征计数（Biamonte 与 Wittek，2017 年，第 195~202 页）。

研究人员还研究了量子计算机在运行神经网络方面的能力。尽管神经网络的稳健表达在量子领域仍然任重道远（Schuld 与 Sinayskiy，2014 年），但学者们已经提出了各种方法来用量子电路来表示经典的神经网络。

例如，来自苏黎世的瑞士联邦理工学院和 IBM Q 的研究人员就经典神经网络和量子神经网络的维数、可最优性和训练性进行了比较。（Abbas 等人，2020 年）

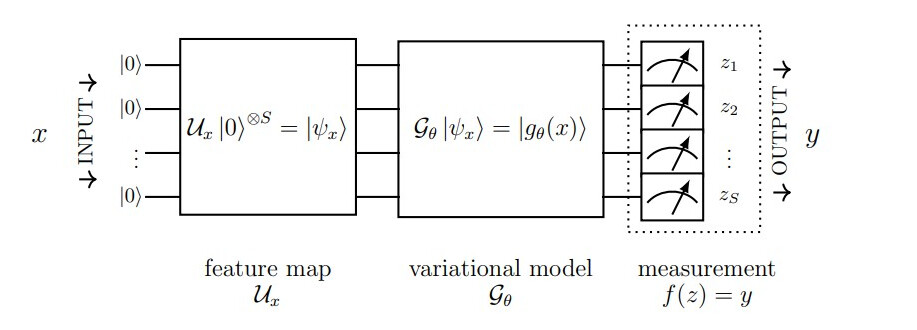
量子神经网络研究

Abbas 等人利用模型的维数来比较不同神经网络的能力。研究结果表明，量子神经网络结合了良好的特征图（对数据进行编码），使其有效维数高于经典神经网络。此外，与经典神经网络不同的是，量子神经网络提供了更好的Fisher 信息矩阵，并且特征值更均匀，不为零。这种量子神经网络在 IBM 的 27 位量子比特机器上的Iris 数据集上，于经典神经网络相比，训练和收敛速度更快。

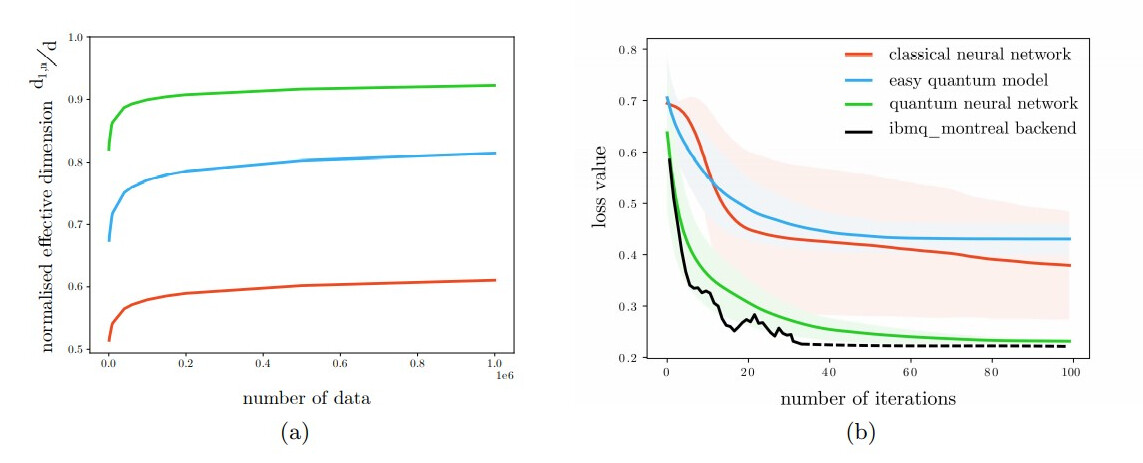
与经典神经网络相比，量子神经网络训练得更好

这些结果表明，具有三段（特征映射、变异和测量）的健壮量子神经网络具有高容量和快速训练性等优势。

NP 困难问题、搜索和蒙特卡洛模拟

量子计算机还擅长于解决优化问题。优化问题利用一种特定的启发式解决方案，从一组有效的解决方案中找到最佳可能的解决方案。为了理解优化如何在量子计算环境下运行，研究人员设计了NP 困难问题的量子算法。举个例子，旅行商问题（Traveling-Salesman-Problem，TSP）中使用的量子算法，它为许多城市提供了比经典蛮力方法更高的二次加速（Srinivasan 等人，2018 年）。

其他利用量子计算机并行性的算法也取得了很有希望的结果。Grovers 算法是目前搜索具有 N 个条目的未排序数据库的最快的量子算法。在经典计算机上，这项任务所需的时间与 N 成正比，但量子计算机显示出平方根加速，并在O(sqrt(N))内完成任务。

类似地，量子计算机可以在 N 个数据点上进行傅里叶变换，反演稀疏 N*N 矩阵，并在时间上求出它们的本征值和本征向量，与 log(N) 中的一个多项式成正比。对于这些任务，已知的最优经典算法所需的时间与 N log(N) 成正比，也就是说，在这种情况下，量子计算机也表现出指数级的加速（Biamonte 与 Wittek，2017 年，第 195~202 页）。

金融行业也正在为量子计算机的潜在应用做准备。分析股票市场及其相关指标的任务可以转化为一个优化问题。有鉴于此，量子计算机的直接实际应用有可能在金融领域扎根。去年 7 月，西班牙 BBVA 银行发布了一项研究报告，结果发现量子计算机能够提高信用评分，现货套利机会，以及加速蒙特卡洛模拟（The Economist 期刊，2020 年）。

同样，摩根大通（JPMorgan Chase & Co.）研究部门负责人 Marco Pistoia 也希望量子计算机可以通过加速资产定价，挖掘表现更好的投资组合以及改进现有的机器学习算法来提高利润。就连高盛（Goldman Sachs）量子研究主管 William Zeng 也大胆宣称，量子计算机能够革新银行业和金融业（The Economist 期刊，2020 年）。

纠缠的未来

量子计算机揭示了一种很有前途的计算和解决问题的新方法。对棘手问题的指数加速比和多项式时间解都是量子比特的量子力学性质的自然后果。这使得计算模型更接近于量子图灵机的抽象模型。

回到我们最初对图灵机的讨论，量子图灵机是经典图灵机的泛化或量子化，其中磁头和磁带是叠加的。形式上，机器的状态是希尔伯特空间（Hilbert space）中的量子态。

量子图灵机的磁带是一个无限长的单边磁带，它代表了叠加的比特。在这种情况下，量子计算是一种幺正变换（unitary transformation），由量子测量决定结果，它将相干叠加中的“单边磁带”简化为经典的“双边磁带”，其具有可分离的正交本征态（Moschovakis，2003 年）。

量子图灵机的图解表示

将这种计算模型与使能硬件结合起来，谷歌展现出的量子霸权被研究界很多人认为违反了丘奇 - 图灵论题的扩展，后者认为这种计算模型应该有效地用经典图灵机建模。事实上，（Bernstein 与 Vazirani，1993 年）论文表明，量子图灵机与传统图灵机有着本质上的不同，它可以解决某些在经典图灵机上需要超多项式时间的问题。

在化学、金融和优化问题中的具体应用，也为量子计算机在现实世界的应用提供了一条途径。此外，量子神经网络令人印象深刻的可训练性和维度为利用量子计算机进行机器学习和深度学习的研究提供了令人兴奋的新途径。

IBM、英特尔、 Zapata、亚马逊和霍尼韦尔等科技公司认识到了量子计算机的潜力，纷纷加大了对其商业应用的投资。用于量子计算机编程的高级语言、框架和库，如 Q#、Qiskit、TensorFlow Quantum 和 Cirq 等，也在稳步增长。

这些框架及其教程已经降低了量子计算开发的入门门槛，如果这一趋势能够持续下去，我们将会在这十年里看到一系列令人振奋的量子计算进展。

尽管取得了这些进展，我们仍需要批判性地思考量子计算机的现状。量子比特对退相干的偏好，加上其高昂的低温要求，给我们现有的硬件带来了极大的限制。所以量子计算机能否真正在实际应用中占据霸权地位，在这个时候提出这个问题可能并不是正确的。更为紧迫的问题是，我们能否克服 NISQ 时代的不切实际之处。

现在看来，这是一个大卫与歌利亚之间的史诗级战斗故事，只是现在宣布这场战争还为时过早。

作者介绍：

Ather Fawaz，是巴基斯坦拉合尔的 FAST 大学本科生，现上大四，主修计算机科学，但对物理和数学也有浓厚的兴趣。他的毕业项目是关于使用生成对抗网络的高保真语音合成。他定期为 Neowin 撰写关于量子计算、人工智能和太空旅行的最新进展。

原文链接：

https://thegradient.pub/knocking-on-turings-door-quantum-computing-and-machine-learning/