加密因特网

因特网的发展带来了企业或个人之间大量的信息交换。信息本身既包含公共信息也包含私有信息，而且大部分信息是以非安全的方式通过超文本传输协议（HTTP ）进行传输的。而少量信息是通过 HTTP 之上的安全套接字层（SSL）进行传输的，即 HTTPS。HTTPS 是一种安全的密码协议，它在 HTTP 之上提供了加密和消息认证的功能。SSL 的引入大大提高了服务提供者的流通处理的成本，其原因是有时需要投资昂贵的终端加速设备。在本文中，我们将展示新技术并显示出使用通用硬件完成大量 HTTPS 传输的实惠。我们的方法分成三段，首先，介绍新 CPU 指令，展示如何使用它们大大加速基本密码操作，包括对称加密和消息认证。其次，展示 RSA 算法的新软件实现的结果，它加速了 HTTPS 协议中的另一个计算密集的部分，也就是公钥加密。第三，展示如何在一个支持 SMT（并发多线程）技术的处理器上均衡 Web 服务器及公钥密算法之间的负载，从而提高 Web 服务器的效率。最后，我们展示这些先进技术能够为 Web 服务提供强大工具，为它们在 HTTP 之上的所有传输大大降低 HTTPS 实施成本。

介绍

到 2009 年 1 月为止，因特网大约连接了 625,000,000 台主机。这些主机之间每秒钟都要进行海量的信息交换，这些数据包含公共信息也包含私有信息，而私有信息往往是机密的并需要受到保护。为信息提供保障的安全协议往往使用在银行和电子商务中，而因特网上的私有信息通常并未受到保护。这些私有信息（除银行和电子商务之外的）包括个人邮件、即时消息、（在网络中）出现、位置、视频流、查询及各种在线社区网络的交互等等，这种忽视主要从经济因素考虑的。安全协议依赖于密码算法，而这些算法都是计算密集的。最后，保护私有信息还要求在线服务的提供者在计算资源上进行很大投入，本文中展示的新技术能够降低在线安全交互的成本，因此可以作为大量服务的选择。

HTTP 之上很多私有数据都是以不安全的方式进行传输的。HTTP 位于 TCP/IP 协议栈的应用层，SSL（Secure Sockets Layer ，安全套接字层）以及后来的 TLS （Transport Layer Security，传输层安全）都是应用层上的安全技术。在文本中，我们只谈论 HTTP 层的 SSL/TLS，也就是 HTTPS。由于先前的 Web 服务器硬件无法处理高流量的 HTTPS 传输中所增加的密码算法的开销，HTTPS 的引入大大提高了 Web 服务提供者处理传输的成本。为了处理这些高流量传输，Web 服务提供者不得不增加昂贵的 SSL/TLS 终端加速设备，这些附加的成本使得 HTTPS 成为 Web 服务提供者的一个备选（或者是高级）方案。结果，大量私有信息的传输都是不安全地进行的，所以，在传输过程中可能被篡改或截获。本文将展现一些新技术，为该问题提供解决的一个途径并显示使用当前的通用硬件完成高流量的 HTTP 传输已成为可能。

本文的组织结构

我们旨在降低已启用了 SSL 的 HTTP 负载的解决方案分成三段。第一，我们讨论了新的处理器指令，并演示了如何使用他们实现基本密码操作的成倍的提速，这极大地降低了 HTTPS 中大规模数据传输时的服务器负载。第二，我们展现了 RSA 非对称密码算法的新实现的结果，它提升了 HTTPS 协议中计算最密集阶段的处理：即，服务器对大量客户端发过来的握手消息进行解密的阶段（下一节描述了 HTTPS 的握手过程的几个阶段）。第三，我们分析了 Web 服务器，分析显示，通过使用了 SMT 技术的处理器均衡 Web 服务器的负载和密码算法的负载可以提高其性能，基于此，我们展示了将密码运算与长延迟时间的内存访问并行执行就能掩盖密码处理所消耗的时间。

随后，我们详细阐述了无处不在地部署 HTTPS 的动机及愿景。首先，我们深入研究了 SSL 过程及其所需资源，然后描述了我们的三段式策略，实验及结果。

动机

我们的研究背后的动机主要是使得 HTTPS 的广泛使用及访问成为可能。这为服务提供者和用户之间建立互信互赢的关系至关重要。信任的一个重要方面来自于他们了解私有沟通是机密的，并且依附于提供者和用户之间建立的原则之上。对于用户，有必要告知并辅导他们，HTTPS 对于在线沟通隐私的益处所在。而服务提供者应该广泛采用 HTTPS 以确保他们能遵守自己的承诺。使用并不昂贵的投资实现 HTTPS 对于创建这样的关系非常重要。

HTTPS 为数据私密及认证提供了一个端到端的解决方案。它保证了当用户从他们的设备向服务提供者传送消息时，他们的消息不会被中间人窃听到。由于任何时间在因特网上传输的消息包都是在不安全的网络上进行的，所以以上保证极为重要。尽管大部分路由设备能躲过直接观察，但是躲不过蓄意窃听者。而那些可公开访问的遍布全球的无线访问点更容易被偷听，这些访问点向他们管理的所有设备广播信息。如果没有端到端的安全解决，这些交互很容易被网络邻居窃听。对于安全问题，还有其他解决办法，比如三层虚拟私有网络（VPN），但是 VPN 往往仅限于中心管理的网络，在这样的网络中用户与其他用户的交互都经过网络中心，即多用户单提供者。在这种情况下，网络提供者已经通过培训的方式向用户传达了严格的数据私密及安全方面的策略。比如，企业内的电子邮件通常仅能通过企业管理的 VPN 进行访问。对于更大的因特网，用户与许多提供者连接。此外，近些年我们看到有利于 HTTP 协议的现象——很多其他交互协议（如 FTP）使用的下降。在这种情况下，HTTPS 是在数量巨大并不断增长的用户和提供者之间提供私密又安全的交互最可行的途径。

将来，HTTPS 的应用可能包括广泛的电子邮件加密、视频流安全、即时消息安全及网络搜索的加密等，这些 HTTPS 的应用在目前并不广泛。此外，一年又一年用户放到网络上的个人私有信息越来越多。云计算使得他们可以在任何地点通过各种设备访问他们的信息。我们相信用户要求他们的提供者用 HTTPS 来保护他们的所有交互是不可避免的。出于为那一天做准备，我们研究和开发了本文中描述的技术。我们展望，有了这些增强，在今天由任何设备发出的基于 HTTP 的交互在不久的将来都可以基于 HTTPS，我们把这称为无处不在的 HTTPS （“ https://everywhere ”）。

安全套接字层（SSL）会话剖析

安全套接字层

安全套接字层（SSL，其后来版本称为传输层安全 TLS）包含了一个握手阶段和加密数据交换阶段。图 1 展示了 SSL 握手的整个过程。在图中，第一阶段， 握手过程开始，客户端向服务端发送一组它可以支持的算法列表和一个随机数，该随机数用作密钥生产过程的输入之一。

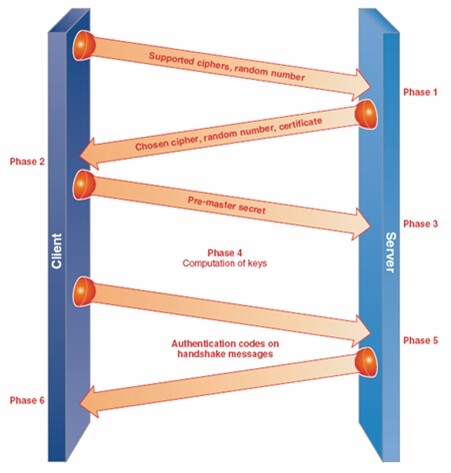
图 1安全套接字（SSL）握手（来源：Intel 公司， 2009）

第 2 阶段，服务端选择其中的一个加密算法回送给客户端，附带包含该服务器公钥的证书，证书用于证明服务器的身份。顺便提一下，服务器的域名也可以通过证书进行校验（这样可以消除钓鱼站点）并向用户表明他们正在与正确的服务端（或服务）进行交互。另外，服务端还提供了第二个随机数，该随机数也作为密钥生成过程的输入之一。第 3 阶段，客户端验证服务端的证书并提取出服务器的公钥。然后，客户端产生一个随机的秘密字符串并使用服务器的公钥对它进行加密，机密后的字符串被称为预主密钥，它被发送给服务器。第 4 阶段，服务器通过 RSA 算法对客户端发过来的加密串进行解密，这是 SSL 交互过程中服务器上的计算最重的过程之一。随后，客户端和服务端各自产生他们的会话密钥，生成密钥的过程中使用预主密钥调用密钥生成函数（key derivatioin function，KDF）两次（该过程中使用了第 1，2 阶段的随机数）。在第 5 和第 6 阶段，SSL 握手以交互双方向对方发送认证码而结束，认证码由所有原始握手消息计算而成。

在 SSL 中，数据以记录的方式传输。记录协议将数据流分解成一组数据段，每一段单独被保护并传输。换言之，在 IPSec 中，数据是以一个 IP 包为基础进行保护的，而在 SSL 中，数据以段为单位进行保护。在段被传输之前，通过计算消息的认证码进行信息保护。段认证码附加在段内容后面，形成消息负载并用服务器（在第 2 阶段）选择的加密算法进行加密。最后，在此负载上加上消息头，消息头与加密的消息体合起来形成记录。

安全的 web 服务器显然是一个极耗内存的应用，对于 SSL 连接而言，其最显著的部分就与密码算法相关，包括使用对称密钥进行包加密、提供消息认证支持以及通过 RSA 建立会话（前文已述）。下面的章节中，我们将更为详细地描述本文中要加速的两个加密算法：高级加密标准（Advanced Encryption Standard ，AES）及 RSA（Rivest Shamir Adleman）。

高级加密标准和 RSA 算法

高级加密标准

AES 是美国政府的对称加密算法标准，它定义在 FIPS 出版物第#197 (2001) [2, 3] 中并广泛应用在具有高吞吐量，高安全需求的应用中。在 HTTPS 中，它可用于为因特网上传输的信息提供机密性。AES 是一个对称加密算法，也意味着在加密和解密消息的时候，使用的是相同的密钥。AES 的结构如图 2 所示：

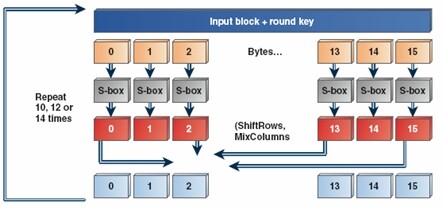
图 2 AES 的结构（来源：Intel 公司，2009）

AES 首先将密钥（可能是 128 位，192 位或 256 位）扩展成密钥排序表，密钥排序表由 128 字节的轮密钥构成，轮密钥用于加密过程中。加密过程本身就是一组被称为 AES 轮的数学转换的演化。

在每个 AES 轮中，输入数据（input）首先与密钥排序表中的其中一个轮密钥进行异或运算。异或运算也可以看成是没有进位的加法。

在该轮加密的下一步，每个 16 字节的 AES 状态经过 S 盒的非线性转换被替换成另一值。AES 的 S 盒包括两个阶段，第一阶段是反转，它不是正常整数算法，而是基于 GF（28）的有限域算法。第二个阶段是仿射变换。在加密过程中，输入的 x 被看成 GF（8）上的元素， 即一个 8 比特向量，它先被反转，然后对反转的结果应用仿射图。在解密的过程中，输入 y 先通过反向仿射图，然后在 GF（8）中反转。 前面提到的 GF（8）反转是在 GF（28）中进行的，它是由不可约多项式定义的，即 p(x) = x8 + x4 + x3 + x + 1 或者 0x11B。

然后，被替换的字节值经过两个线性转换，分别是 ShiftRow 和 MixColumn。ShiftRow 仅仅做字节置换，MixColumn 转换操作在 AES 状态的矩阵表示的列上进行。每一列由一个矩阵乘法得到的值进行替换，加密过程中所使用的转换如方程 1 所示，在该方程中，根据 GF（28）的规则进行矩阵与矢量的乘法，使用的是 S 盒中相同的不可约多项式，即是，i>p (x) = x8 + x4 + x3 + x + 1。

解密过程中，反向 ShiftRow 跟在反向 MixColumn 之后，反向 MixColumn 转换的如方程 2 所示。

注意到 MixColumn 转换用 1，1，2 和 3 与每列中的字节相乘，而方向 MixColumn 用的则是 0x9, 0xE, 0xB, and 0xD。根据密钥大小（128，192，256 比特）的不同，相同的过程要进行 10，12，或 14 轮。最后一轮 AES 省略 MixColumn 转换。

RSA 算法

RSA 是一种公钥密码算法设计。公钥算法背后的主要想法是加密技术可以有后门的存在。后门的意思是指，密码只需要交互的一方知道，这样可以简化加密流程。在公钥算法中，消息通过公钥加密，而一个公钥对应一个私钥。在不知道私钥的情况下，很难解密消息，类似地，攻击者也很难发现信息原文。

为了进一步解释公钥算法，我们以 RSA 算法做例子来说明。在该算法中，交互双方选择两个随机的大数 p 和 q，为了安全的最大化， p 和 q 长度应该相同，然后交互双方如下计算：

对于某些 l，D 和 E 可以互换使用，也就是说可以使用 D 加密，而使用 E 进行解密。

RSA 的典型实现使用中国剩余理论，它可以将一个模数的取幂运算减低成对长度是它的一半的两个数的取幂操作，以此类推，通过使用平方乘的技术可以将取幂操作化解成模数平方及模式乘运算的序列。平方乘运算还可以增强，并使用某些视窗法降低模数乘运算的次数。最后，模数平方和乘运算可以通过如 Montgomery 或 Barrett [4, 5] 这样的简约算法简化成大数的乘法运算。

加速技术

我们正在研究成倍提升 HTTPS 会话速度的方法来实现加密因特网的愿景。下一代微系统结构新增的指令可能会将对称加密算法提速 3-10 倍。这些指令不仅提供了更好的性能，还能保护应用免受边道攻击（side-channel attack）的威胁。其次，我们已开发出改进的整数运算软件，它可以将密钥交换及构造过程提速达 40-100 倍。

第三，Intel® Core™ i7 微体系结构再次将 SMT 技术引进 CPU 中，对于将计算密集的公钥加密软件的运算周期隐藏在网络应用内存查找的延迟时间内 SMT 是非常理想的。

新处理器指令

下一代 Intel 处理器将引入一组新指令，它们将支持高性能及安全的轮加密和轮解密。这些指令是 AESENC（AES 轮加密），和 AESENCLAST（AES 最后一轮加密），AESDEC（AES 轮解密）以及 AESDECLAST（AES 最后一轮解密）。还引入了另外两个用于实现密钥排序表转换的指令，AESIMC 和 AESKEYGENASSIST。

这些新处理器指令的设计基于 AES 的结构。AES 这样的系统包括复杂的数学操作，比如有限域乘法与反转 [6]（前文已述）。这些操作用软件实现需要消耗更多的时间及内存，但是用组合逻辑实现时则更快，且更加节能。另外，有限域操作的操作数能够适合 IA 体系结构的 SIMD 寄存器。本文中，我们讨论使用组合逻辑将整个 AES 轮实现为单个 IA 处理器指令的概念。一个 AES 轮指令比等同的基于表查找的软件程序要快很多，并且可以流水化，所以有可能在一个时钟周期内计算出一个独立的 AES 轮的结果。

这些 AES 指令可以看成是密码算术的原语，它们不仅可用于 AES 的实现，还可以用于广泛的密码算法。例如，最近的 HIST SHA-3 哈希函数竞赛中就有不少提案使用了 AES 轮作为计算密码哈希值的基础元件。另外，指令调用的合并还可以用于创建更加通用的有限域计算的原语。这些新指令在相同的平台上与最好的软件实现相比，在处理相同的数学操作的情况下要快 3-10 倍。

与这些 AES 指令一起，Intel 将提供另一个新指令用于支持无进位乘法（carry-less multiplication），称为 PCLMULQDQ。该指令执行两个 64 位四个字的无进位乘法运算。这两个操作数是根据中间字节值选择出来的第一和第二个乘数。

无进位乘法，又称为 Galois 域（GF）乘法，在该操作中对两个数进行相乘是不产生和传递进位。在标准的整数乘法中，第一个操作数移动的次数等于第二个操作数中值为“1”的比特位的个数，每次移动的距离就是“1”在第二个操作数中的位置。两个数的执行结果由所有移动后的第一个操作数相加而来的。在无进位乘法中，过程依然相同，但是相加时不产生进位也不传递进位。这样，比特加操作就相当于逻辑操作中的异或（XOR）。

无进位乘法是很多系统和标准（包括时钟冗余校验，CRC，Galois/ 计数模型，GCM 和二进制椭圆曲线等）的计算的一个非常重要的组件，该操作在当今处理器上用软件实现时效率极为低下。所以，加速 Carry-less 乘法的指令对于 GCM 和所有依赖于它的交互协议 [8] 来说相当重要。

改进的密钥构造软件

我们还开发了整数算法软件 ，他至少可加速大数乘以及模数减运算达 2 倍。这些程序不仅用于 RSA 公钥加密，还可用于 Diffe Hellman 密码交换以及椭圆曲线密码算法（ECC）。使用了我们的软件在 Intel® Core i7 处理器上 RSA 1024 的性能可以从大概每秒处理 1500 个签名（OpenSSLv.0.9.8g）或者 2000 个签名（OpenSSL v.0.9.8.h）提升到每秒 2900 个签名。类似地，我们还可以加速其他流行的密码模式，如 RSA 2048、和基于 NIST B-233 曲线的椭圆曲线加密 Diffie-Hellmn。

RSA 的性能可以通过提升大数乘法的速度而提升，因为它是该算法中计算最密集的部分。我们的实现使用了优化的背包大数相乘算法。RSA 算法是计算非常密集的算法，它要消耗数百万的时钟用于执行 64 位数的乘法，加法和减法。然而，RSA 所存储的状态却很小，只包含一些关键信息及 16 至 32 个能够放入 Intel CPU 的一级缓存（cache）中的乘数。使用了我们的软件，RSA 1024 解密操作在 Intel® Core i7 处理器上只消耗了 99 万时钟，而相应的 RSA 2048 解密操作消耗了 673 万时钟。这个速度比 OpenSSL（v. 0.9.8h）执行相同操作要快 40%。

下图中列出的代码描述了主要思想，它通过对中间数（check）利用寄存器回收技术将乘法和加法操作合并起来。在代码 1 中，“a”和“b”保存了相乘的两个大数，结果存在“r”中。这些操作对所有输入不断重复，并产生中间数，这些中间数相加后得到大数相乘的结果。

<img _href="http://www.infoq.com/resource/articles/encrypt-internet-intel/en/resources/Code1.bmp" _p="true" alt="" src="http://www.infoq.com/resource/articles/encrypt-internet-intel/en/resources/Code1.bmp"></img>代码 1 RAS 实现（来源：Intel 公司，2009）

我们还研究了其他大数相乘的技术，包括类 Karatsuba 构造，但是我们发现这个背包算法实现是最快的 [9,10]。

并发多线程技术

最新的 Intel® Core i7 微体系结构再次引入了超线程（现在被称为并发多线程或 SMT）的技术。SMT 是该处理器与此前的核心微体系结构的最大差别，因为这些核心都是单线程的。作为研究的一部分，我们演示了 SMT 可以为一类特定的工作负载带来根本性性能提升，这些工作负载与安全 Web 事务相关。我们提出了一种新的编程模型 ——使用一个计算密集的线程只进行 RSA 公钥加密操作，另一线程进行内存存储密集的操作。我们发现当使用 SMT 时，RSA 线程可以作为四个典型的内存存储密集的工作线程的理想伙伴，并可以带来 10% 至 100% 的潜在性能提升。

当执行独立内存查找的线程与 RSA 线程相伴执行时系统可获最多益处。内存线程的吞吐率几乎翻倍，达到了没有 RSA 伴随情况下的值。对该结果的另一种解释是 RSA 计算几乎没有消耗时间，这都功因于 SMT。在现实中，RSA 计算被隐藏在内存线程的长延迟时间期间。我们还观察到当 SMT 开启，当一个内存线程与另一个内存线程相伴执行时，单个内存线程的吞吐量大约提高了 30%，而当与 RSA 算法相伴执行时，吞吐率翻倍。这些结果指明 RSA 算法比第二个内存线程更适合作为陪伴线程，原因是一个工作是内存访问密集型，而另一个是计算密集型。当一个 RSA 线程与一个内存线程相伴执行时，SMT 开启时 RSA 的性能比 SMT 关闭时性能提升 21%[11]。

为了进一步验证我们的观点——SMT 特别有助于密码工作负载，我们创建测试了一个运行 SpecWeb* 2005 的测试台。测试台的组成是一台 Intel® Core i7 处理器的服务器，连接到两台客户机，在上面一共运行了四个客户端引擎。我们测量了 SMT 开启和关闭时的服务器处理的 Banking(HTTPS) 和 Support(HTTP) 工作负载的能力。实验表明 SMT 对整体系统性能至少提升了 10%，而 Banking 工作负载比 Support 工作负载提高的更多。该结果与我们前面的实验相吻合，并且也表明了密码工作负载也能利用 SMT 的优势。

我们的密码算法加速技术的整体影响如图 3 所示，第一栏是 230K 字节的 SSL 交易运行在今天的 Intel® Core i7 处理器上的负载。加密模式使用了 AES-256 的反模式（counter mode）。第二栏显示了使用新指令实现 AES 时获得的加速效果。第三栏展示了使用我们的 RSA 软件及 SMT 之后的加速结果。最后一栏展示了将 SHA1 替换成 GCM 后的结构。GCM 是一种提供了与 HMAC-SHA1 相同功能的消息认证模式。在图中可以明显看到，我们的加速技术从根本上减低了密码工作负载并带来了性能及效率显著提高。

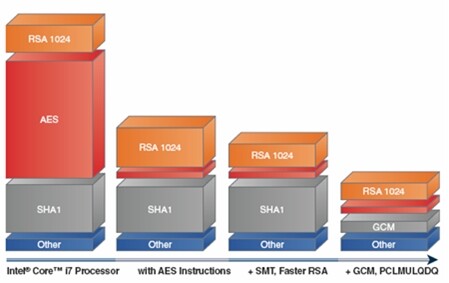
图 3 密码加速技术的影响（来源：Intel 公司，2009）

结论

总之，Intel 正在研究提供成倍提升密码算法速度的新技术。我们描述了可以提升 AES 对称加密速度的新处理器指令，该提升从根本上减低了 HTTPS 处理大块数据传输时的服务器负载。我们还展现了 RSA 非对称密码算法的新实现，它加速了 HTTPS 协议的计算密集型阶段，即服务器必须解密来自大量客户端的握手消息的阶段。第三，我们分析了 Web 服务器并展示了一些初期实验，结果表明，通过在支持 SMT 技术的处理器上均衡 Web 服务器负载和密码算法负载可以提升服务器的效率，它显示了密码算法负载可以隐藏在并行处理的内存访问的长时间延迟期间。我们的最终目标是使通用处理器能够高速处理及转发加密的信息传输，从而让因特网逐步转变成为完全安全的信息交付基础设施。我们还相信这些技术有益于其他使用模型，比如硬盘加密和存储等。

参考

[1] R.L. Rivest, A. Shamir, and L. M. Adleman. “A Method for Obtaining Digital Signatures and Public-Key Cryptosystems.” Communications of the ACM, 21,2, pages 120–126, February 1978.

[2] V. Rijmen. “Efficient Implementation of the Rijndael S-box.” At http://www.google.com

[3] “Advanced Encryption Standard.” Federal Information Processing Standards Publication 197. At http://csrc.nist.gov

[4] P. Montgomery. “Multiplication without trial division.” Math. Computation, Volume 44, pages 519—521, 1985.

[5] P. Barrett. “Implementing the Rivest Shamir and Adleman Public Key Encryption Algorithm on a Standard Digital Signal Processor.” Masters Thesis, University of Oxford, UK, 1986.

[6] S. Gueron, O. Parzanchevsky and O. Zuk. “Masked Inversion in GF(2n) Using Mixed Field Representations and its Efficient Implementation for AES.” Embedded Cryptographic Hardware: Methodologies & Architectures. Nadia Nedjah and Luiza de Macedo Mourelle (Editors), Nova Science Publishers, Inc.(ISBN: 1-59454-012-8), 2004.

[7] S. Gueron. “Advanced Encryption Standard (AES) Instructions Set.” At: http://software.intel.com/

[8] S. Gueron and M. Kounavis. “Carry-Less Multiplication and Its Usage for Computing the GCM Mode.” At http://software.intel.com/

[9] A. Karatsuba and Y. Ofman. “Multiplication of Multidigit Numbers on Automata.” Soviet Physics—Doklady, Volume 7, pages 595–596, 1963.

[10] M. E. Kounavis. “A New Method for Fast Integer Multiplication and its Application to Cryptography.” In Proceedings 2007 International Symposium on Performance Evaluation of Computer and Telecommunication Systems. San Diego, CA, 2007.

[11] S. Grover and M. Kounavis. “On the Impact of Simultaneous Multithreading on the Performance of Cryptographic Workloads.” Technical Report, available from the authors upon request.

本文及更多类似的主题可以在 Intel 技术期刊，2009 年六月版的“因特网安全的提升”一文中找到。更多信息请参考 http://intel.com/technology/itj 。

关于作者

Satyajit Grover 是一个 Intel 实验室的软件工程师。日常工作涵盖安全和完整性（integrity）。在 Intel，他在这个领域已经有工作两年多。在此之前他是 Portland 州立大学的计算机科学系的研究生及助理研究员。他的邮箱是 atyajit.grover at intel.com。

Xiaozhu Kang 是 Intel 实验室的研究科学家。她的研究兴趣包括算法设计和性能分析。她在 2008 年获得 Columbia 大学电子工程学的博士学位，并与 2009 年 1 月加 入 Intel。在此之前她曾是 Intel，Mathworks 及 NEC 实验室的实习生。她的电子邮箱是 xiaozhu.kang at intel.com。

Michael Kounavis 是 Intel 实验室的高级研究科学家。他负责主持旨在提升广泛的客户端、服务端以及网络应用速度的新型数字算法及密码算法。Michael 是 CRC32 SSE4 指令的合作发明者，该指令用于 iSCSI CRC 时代的 Intel® Core i7 体系结构中。由于 AES 指令方面的工作，他还是 2008 Intel 成就奖的共同获奖者。他的电子邮箱是 michael.e.kounavis at intel.com。

Frank Berry 是 Intel 实验室的首席工程师。他所专长的领域是硬件 / 软件接口，即硬件和软件紧密连接之处。此外，他的专长还包括操作系统内核，设备驱动程序，网络协议栈等。Frank 在 InfiniBand 体系结构及 AES 指令方面的工作为他赢得了两次 Intel 成就奖。他的电子邮箱是 frank.berry at intel.com。

阅读英文原文： Encrypting the Internet 。

感谢黄璜对本文的审校。

给InfoQ 中文站投稿或者参与内容翻译工作，请邮件至 editors@cn.infoq.com 。也欢迎大家加入到 InfoQ 中文站用户讨论组中与我们的编辑和其他读者朋友交流。