Base-x 编码的奥秘

Base Encoding 是一组二进制转文本的编码模式（Encoding Scheme），常见的有 Base64、Base58、Base32、Base16。大家不仅疑惑为什么需要二进制转文本这种编码模式呢？常见误解之一就是既然所有的编码最终都会变成 0 和 1，那么分成 ASCII 和 Base64 编码是不是就没有必要呢？

Base 编码的历史

1970~1980 年代，DEC（和其他公司）生产的“微型计算机”使用的字符编码为 ASCII。每个字节使用 7 位，给出 128 个可用值。这足以满足大写和小写拉丁字母，数字，标点，一些常见的数学符号，货币符号和控制字符的需要。此后 ASCII 变得非常流行，并在很长一段时间内占主导地位。ASCII 规定了范围在 [0,127] 之间的字符编码，其中 [0, 31] 以及 127 (del) 这 33 个属于不可打印的控制字符（可以使用 man ascii 查证）。互联网的杀手级应用——电子邮件系统当初是为了传输 7 位 ASCII 文本而设计的，于是在传输信息时，有些邮件网关会把 [0,31] 这些控制字符给清除，而有些会替换 10 (newline 或 \n）和 13 (carrige 或 \r) 字符，有些更加粗暴地将二进制的最高位清空，还有的程序在收到 [128, 255 ] 之间的国际字符会发生错误。

如何在不同邮件网关之间安全地传输控制字符、国际字符和二进制文件呢？作为 MIME（RFC 2045 和 RFC 3548）多媒体电子邮件标准的一部分的 Base64 编码就被开发出来了。

Base64 编码的解题思路很简单。既然直接传输控制字符、国际字符和二进制文件容易造成原始信息在传递过程中的错误，那么就把原始信息都转成 ASCII 的可打印字符，这样就能让旧系统安分点，不再胡乱改变其内容。

Base64 是怎么做的呢？它的核心算法是将每 3 个字节（3 * 8 = 24 比特）依次转换成 4 个可打印字符（4 * log 64 = 24 比特）。具体操作如下：

1. 将 3 字节的数据，先后放入一个 24 位的缓冲区中，先来的字节占高位。数据不足 3 字节的话，缓冲器中剩下的比特用 0 补足。

2. 每次取出 6 比特，按照其值选择 ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/ 中的字符作为编码后的输出，直到全部输入数据转换完成。

3. 若原数据长度不是 3 的倍数时且剩下 1 个输入数据，则在编码结果后加 2 个 =；若剩下 2 个输入数据，则在编码结果后加 1 个 =。用来代表补足的字节数。

我们以换行字符（ASCII 码 10）为例，原始的二进制表示如下

1. 10 的二进制表示是 0000 1010，放到 24 位的缓冲区补零为 00001010 00000000 00000000

2. 每次取 6 比特，则如右边划分所示：000010 100000 000000 000000。因为后两部分为补零，适用于规则 3。前两部分的十进制依次是 2, 32，所以通过索引表选择的值是 C, g

3. 后两部分是补零，所以替换成=。

4. 故结果为 Cg==

为什么需要 Base58？

首先，Base58 和 Base64 一样都是一组二进制转文本（binary-to-text）的编码模式。Base58 的主要职责是将大整数表现成文本，它是由中本聪在 Bitcoin 中首先引入进来的。为什么要这样使用呢？有如下几个原因：

https://en.bitcoin.it/wiki/Base58Check_encoding#Background

// Why base-58 instead of standard base-64 encoding?// - Don't want 0OIl characters that look the same in some fonts and//      could be used to create visually identical looking account numbers.// - A string with non-alphanumeric characters is not as easily accepted as an account number.// - E-mail usually won't line-break if there's no punctuation to break at.// - Doubleclicking selects the whole number as one word if it's all alphanumeric.

1. 去掉了 Base64 中的长相相近的字符，这样直观上就能分辨账户数字，如：0（零）和 O（大写 o），I（大写 i）和 l（小写 l），以及 + 和 / （non-alphanumeric 非字母和数字组成的），共 6 个字符。这也是 Base58 名称的由来，因为 64 - 6 = 58

2. 非字母和数字的字符就不太容易混入账户地址里

3. 在邮件里没有标点就不会断行（意在排除截断的可能性）

4. 双击就能全部选中所有字符和数字的串

顺带一提，Base56 相较于 Base58，少了 1（一）和 o（小写 o）这两个字符，而 Base32 则只包含 A-Z 和 2-7 这 32 个字母和数字。

Base58 的特点

维基百科上说，Base58 不太适合编码二进制数据，而适合编码大整数？在探讨 Base58 的实现原理之前，我们先看看比较常见的几种 Base 编码。

Base16

有人可能会说 Base16 我没有用过，怎么能说常见呢？乍看这个名字还挺唬人的，但其实它就是 Hexidecimal 十六进制编码。对于 10101010，会被编码成 0xAA。拆解来看，1010 是十进制的 10，也就等于十六进制中的 A。原因是十六进制只能表示 0-9 以及 A-F 这 16 个数，16 换成二进制的范围就是 0000 - 1111。

Base32

那么 Base 32 这种编码呢？同理，它可以表达的二进制范围是 00000 - 11111 也即 2 的 5 次方，即 32 个数。但问题是二进制都是 8 位起，8 是没法整除 5 的。既然 8 除以 5 除不尽，那我们就找 8 和 5 的最小公倍数，即 40。换句话说，5 bytes = 8 chars。也就是说，我们需要将每 5 个字节转化成 8 个 Base32 中的字节。

由此，我们可以总结出一些规律。Base16 这种编码方式，8 和 4 的最小公倍数是 8，所以 1 bytes = 2 chars，每次都能将一个字节转化成 2 个字符，都能刚好对齐。而 Base32 这种编码方式，因为 8 和 5 的最小公倍数是 40，所以 5 bytes = 4 chars，存在对齐不了情况，那么非 5 字节倍数的字节序列就需要额外补齐，同理， Base58 和 Base64 也需要如此。

Base58

继续深入之前，我们先回忆一下中学学习的短除法求解二进制。以 10 为例，计算如下：

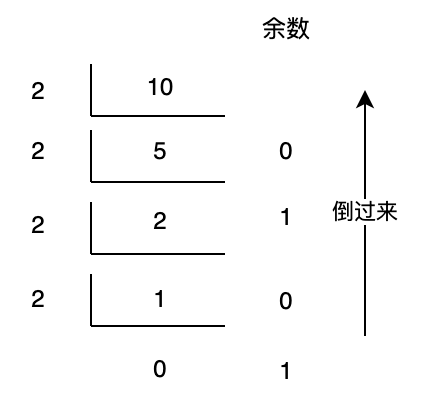
图 1 短除法计算十进制转二进制

短除法的实质是连除进制，降低位权，依次得到各位上的数值。我们不妨以十进制的 111 举例。

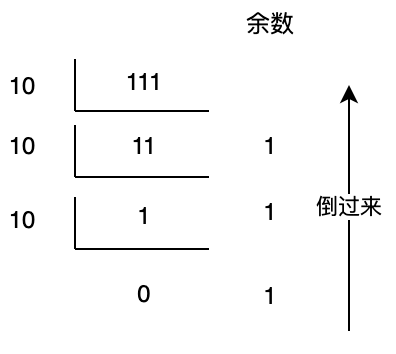
图 2 短除法计算十进制数各位上的数值

虽然上面的计算纯属画蛇添足，不过它对于理解二进制的短除法还是很有帮助的。我们第一次用 111/10，得到的余数为 1，便是个位上的数；再次用 11/10，得到的余数为 1，便是十位上的数；最后用 1/10 得到的余数为 1，就是百位上的数。类比可得，上例中计算 10 这个数字的二进制时，第一次用 10/2，得到的余数 0 便是最低位上的数，得到的商为 5，则是 10 这个数的二进制 1010 的高三位（101），依次类推即可得到不同数位上的二进制数了。所以这样就不难理解短除法有效性的来源。

我们再来看看 Base58 这种编码方式，它有 58 个字符，所以可以表示的二进制范围是 000000 - 111001。因此，Base58 编码算法需要除法运算实现，如果被编码的数据较长，则要用特殊的类来处理大数，在 Bitcoin 使用了 OpenSSL 中的 BIGNUM。

伪代码 - Base58 利用短除法编码的过程

code_string = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz";x = convert_bytes_to_big_integer(hash_result);
output_string = "";
while(x > 0){  (x, remainder) = divide(x, 58);  output_string.append(code_string[remainder]);}
repeat(number_of_leading_zero_bytes_in_hash){  output_string.append(code_string[0]);}
output_string.reverse();

小结

Base64 用于编码邮件内容、网页图片，意在减少传输过程中可能出现的错误；Base58 是比特币地址使用的编码方法，旨在提高地址的辨识度；Base32 用在一些对大小写不敏感的文件系统中。每种 Base-x 的编码都有适合它们的应用场景。自然，为应对需要我们也可以发明自己的 Base 编码。

本文转载自：ThoughtWorks 洞见（ID：TW-Insights）

原文链接：Base-x 编码的奥秘