点评可调整大小哈希表：Riak Core 和随机切片技术

本文要点

• 哈希表是一种用于管理空间的数据结构。它最初用于单一应用的内存，之后应用于大规模的计算集群。
• 随着哈希表在一些新领域的应用，原有的哈希表大小调整方法存在一些不好的副作用。
• 亚马逊公司于 2007 年发表的 Dynamo 论文提出将一致性哈希技术应用于键值存储。Dynamo 类型的一致性哈希很快被 Riak Core 及其它一些开源分布式系统采纳。
• Riak Core 一致性哈希的实现具有一系列局限性，导致在集群规模更改时出现问题。
• 随机切片是一种非常灵活的一致性哈希技术，避免了 Dynamo 类型一致性哈希中存在的所有局限。

今年秋天，Wallaroo Labs 将发布其分布式流数据处理框架 Wallaroo 的一系列新功能。其中一项新功能是支持调整计算群集的规模，实现该功能需要一种大小可调整的分布式数据结构。一个好的做法是使用分布式哈希表。但问题在于，我们应该如何选择分布式哈希算法？

使用一致性哈希技术建立可调整大小的分布式哈希表已有 20 多年的历史。看上去似乎一致性哈希能很好地适用于 Wallaroo 的情况。鉴于此，本文将探讨一致性哈希是否的确适用。文章的结构如下：

1. 简介一致性哈希试图解决的问题，即在实现调整哈希表大小的同时，尽量降低不必要的数据移动。
2. 概述 Riak Core 一致性哈希的实现。
3. 指出 Riak Core 哈希在 Riak 环境中及在满足 Wallaroo 对一致性哈希实现需求上的一些局限性。
4. 通过大量的示例和插图，介绍随机切片（Random Slicing）技术。

引言：问题在于如何调整哈希表大小

大多数程序员都熟悉哈希表。对于初次接触哈希表的人而言，推荐阅读维基百科中哈希表的相关文章。本文中仅对此给出一个概要介绍。非常熟悉哈希表的读者可直接跳到本节末尾的图一。文中还使用了几个类似的图，用于说明一致性哈希方案。

哈希表是一种组织计算机内存的数据结构。对于键“key”，如何确定存储 key 相关联值“val”的位置？

下面的伪代码来自维基百科文章：

let hash = some_hash_function(key)      ;; hash is an integer
let index = hash modulo array_size      ;; index is an integer
let val = query_bucket(key, index)      ;; val may be any data type

一个哈希表通常包含上述三个基本步骤。其中，前两个步骤首先将 key（可以是任意数据类型）转换为一个非常大的数值（即例子中的变量hash），然后再转换为一个相对更小的数值（例子中的变量index）。后者通常称为“桶索引”（bucket index），因为它在哈希表的具体实现中通常使用数组实现。变量index的值通常使用取模运算计算得到。

一些类型的哈希表在一个桶中存储单个值。因此，桶的总数（即上例中为array_size）是一个非常重要的常量。但是如果桶的规模是一个常量，那么我们应该如何调整哈希表的大小？做法很简单，允许array_size作为一个变量而非一个常量即可。但是这时如果继续使用取模运算计算index桶的编号，由于array_size的大小可调整，哈希表依然存在着问题。

下面，我们将哈希表的桶数由 3 改为 10，然后查看一下前 24 个哈希值，即从 0 到 23。

图一 使用取模算法将哈希值分配给桶的图示

在图一的最左端，哈希值 0、1、2、3 所指派的桶并未发生变化。但是当取模算法再次“转回”到桶 0 时，此后的指派全部发生了变化。读者们可以看到一条从“（hash=4, buckets=3）”开始延伸到图右端的红色对角线。如果我们调整了桶的数量，那么该对角线右侧的大部分值也相应地发生了移动！

随着array_size值的增加，值移动问题会加剧。尤其是当array_size从\(N\)增加到\(N+1\)时，只有\(\frac{1}{N}\)的值依然位于原来的桶中。而我们希望发生的情况正相反，我们希望只有\(\frac{1}{N}\)的值移动到新桶中。

一致性哈希是一种能提供预测哈希表大小调整行为的方法。下面我们介绍一种特定的一致性哈希实现，并给出哈希表调整操作。

一致性哈希和 Riak Core 简史

哈希表传统上是一种用于组织计算机内存空间的数据结构。1997 年，阿卡迈公司（Akamai）的研究者们发表了一篇影响深远的论文，名称是“一致性哈希和随机树：一种用于万维网上热点问题的分布式缓存协议”（ Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web ）。论文提出使用哈希表实现对另一种类型空间的组织，即 HTTP 服务器集群的缓存。

在 SOSP 2007 上，亚马逊公司发表了名为“Dynamo：亚马逊公司的高可用键值存储”（ Dynamo: Amazon's Highly Available Key-value Store ）的论文。受该论文的启发，Basho Technology 公司的创始者们创立了一种 Dynamo 的开源实现，称为 Riak 键值存储。在亚特兰大召开NoSQL East 2009 大会上，Justin Sheehy 通过演讲首次公开介绍了Riak 。此后， Riak 的核心软件库代码从 Riak 数据库分离出来，并作为独立的分布式系统平台使用。

我注意到 Damian Gryski 在今年（2018 年）早期撰写的一篇博客文章，“一致性哈希：算法上的权衡”（ Consistent Hashing: Algorithmic Tradeoffs ）。我推荐大家阅读该文，文中介绍了一致性哈希功能的一些其它实现方法，并给出了对比情况。

Riak Core 的一致性哈希算法

目前有大量介绍如何使用 Riak Core 一致性哈希算法的资料。本文将通过例子做一个概要介绍，目的是为了引出后文对 Riak Core 哈希方法局限性的讨论。

文中引用了 Justin Sheehy 最早演讲中使用的几个示意图。第一个示意图显示了一个具有 32 个分区的哈希环，各个分区分别指派给 4 个节点。Riak Core 使用 SHA-1 算法将哈希字符串转换为整数。SHA-1 的输出大小为 160 位，可以直接映射到整数范围\(0\cdots 2^{160}-1\) 。

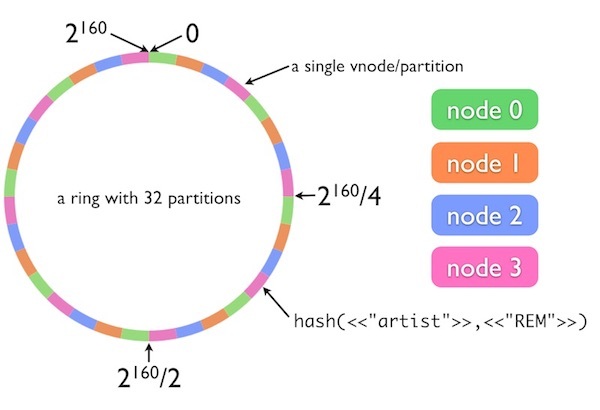
图二 一个具有32 个分区的Riak 环，间隔分别指派给4 个节点

在 Riak Core 的数据模型中，命名空间被分隔为“桶”（bucket）和“键”（key），这不同于我在本文最后一节所使用的定义。本例中使用了名为“artist”的 Riak 桶和名为“REM”的键。我们将这两个字符串连接在一起，作为 Riak Core 一致性哈希函数的输入。

在本例中，哈希环被分隔为同等大小的 32 个分区，平均分配给四个服务器节点，即每个节点指派了 8 个分区。字符串“artist”+“REM”通过 SHA-1 映射到哈希环中大约 4 点钟的位置。可以看到，node3（粉红色节点）分配给哈希环该部分。如果不考虑数据副本，那么我们可以说 node3 就是负责存储键“artist”+“REM”对应值的服务器。

下面考虑在第二个例子中添加数据副本。如果 node3 崩溃了，会发生什么？这时应该如何定位存储键所对应值的副本？

图三 在32 个分区环上的Riak get 查询

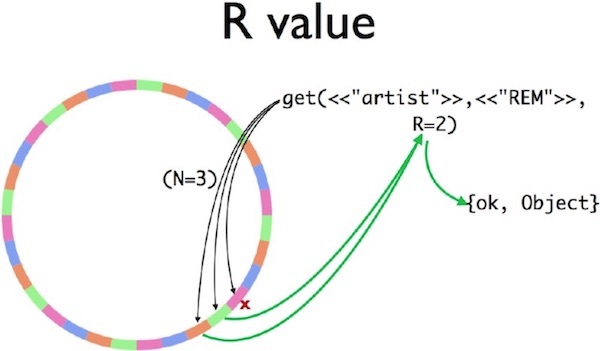
Riak Core 使用了多个常量描述数据副本的存储位置，其中包括每个键对应值的副本总数 N，以及从数据库成功获取键的最小服务器查询数 R。为计算确定对应于单个键的所有服务器，哈希算法采用“顺时针在环上行走”，直至找到 N 个不同的服务器。在例三中，副本集被粉红色、绿色和橙色服务器处理（即 node3、node0 和 node1）.

如果图中的 node3（红叉标识的粉红色分区）已经崩溃，这时 Riak Core 客户发送查询到 N=3 的服务器，node3 并不会响应。但是来自 node0 和 node1 的副本足以满足 R=2 的约束。客户响应将是成功回复{ok,Object}。

Riak Core 一致性哈希算法的约束和局限

我曾在 Basho Technologies 公司任高级软件工程师达六年。通过自身的一些事后反思，以及与不少 Basho 前同事的讨论，在此我对 Riak Core 一致性哈希算法做出尽量客观的批评。我支持 Basho 继续保留这些我称之为局限性甚至可以说是缺陷的问题，因为它们在当时都是合理的权衡考虑。我们现在的看法都是一些后见之明，并且我们也有时间去反思学术界和工业界的新发现。Basho 公司于 2017 年被清算，其源代码资产出售给英国的 Bet365。Riak Core 的维护工作仍继续在其所有者 Bet365 和 Riak 开源社区中进行。

下面列出了 Riak Core 在实现 Dynamo 风格的一致性散列算法中的一些假设和局限性。列表的排序是大致按问题在 Basho Technologies 公司的严重性、麻烦程度、触发客户支持工单数以及升级情况。

1. 仅使用 SHA-1 作为字符串转整数的哈希算法。
2. 哈希“环”的整数间隔范围是 0 到\(2^{160}-1\)。
3. 分区数是固定的。
4. 分区数必须是 2 的指数次幂。
5. 每个分区的大小是固定的。
6. 从历史上看，用于将服务器指派给哈希环上各个间隔的“声明指派”（claim assigment）算法考虑过于简单，并存在错误，经常在给出节点间不平衡的工作负载。
7. 没有考虑按“权重值”调整服务器的容量。所有服务器均假定是平等的。
8. 不支持对极端“热门”键（类似于 Twitter 上人气最旺的“Justin Bieber”帐户）的隔离。
9. 对“机架可感知”或“出错域可感知”的副本放置策略缺乏有效的支持。

其中，局限性 1 和 2 并非大问题，它们都与使用 SHA-1 哈希算法相关。160 位的有效哈希范围足以适用于我所知道的所有 Riak 用例。有大量 Basho 客户想要用其它算法替换将 SHA-1 算法。Basho 支持团队的官方回应总是，“我们强烈建议您使用 SHA-1”。

局限性 3 到 5 曾在一段时间内有影响，但是它们已在很久以前被清除了。这些局限性的存在，一开始人们的理由是“Dynamo 就是这么做的”。此后理由成为“Riak 代码最初就是这么做的”。在创建了 Riak Core 软件库后，理由变成“这都是一些没有人愿意碰的遗留代码”。抱歉，在此我不一一展开介绍，具体原因偏离了本文的主题。

局限性 6 到 9 曾对那些优秀的 Basho 客户支持工程师和开发人员造成了很大的麻烦，最终影响了 Basho 的市场和业务发展。存在缺陷的“声明指派”（局限性 6）导致了严重的数据迁移问题，即当数据需要从 X 个服务器移动到 Y 个服务器时，会在一些机缘巧合的 X 和 Y 组合上出现问题。非常难以实现将原来的 Riak 集群从一些更旧更慢的硬件迁移到更新更快的机器（局限性 7），因为在哈希环指派中 Riak Core 假定所有的机器具有同样的 CPU 和磁盘容量。尽管这些缺陷可以通过人工解决，但是几乎每次都需要 Basho 支持团队的参与。

对于“Justin Bieber”现象（局限性 8），即在某个“热”键上的查询数呈数量级地高于其它键，Riak Core 对此束手无策。因为 Riak Core 分区的大小是固定的，将同一分区的任何键作为超级热键，这都会导致性能降低。唯一的缓解方法是迁移到具有更多分区的哈希环，但这样做违反了局限性 3。该问题可以（在 Basho 支持的帮助下）人工解决，但是需要做人工干预指派（服务器按顺时针顺序指派给哈希环），将热键分区指派给更大更快的机器。

局限性 9 是一个长期存在的市场和业务扩展问题。为每个对象维持 N 个副本，对此 Riak Core 通常很少存在问题。作为一个最终一致的数据库，Riak 为避免出错采取了一种更保守的做法，即对每个对象制作多于 N 个副本，然后在自动“切换”过程中复制并合并副本。

但是，Riak Core 的声明指派并不支持“机架可感知”和“出错域可感知”。通用电力支持、网络路由器及其它通用基础设施故障，会导致多个副本同时失败。为支持单个静态数据中心的配置，有时我们需要手工创建“在哈希环上顺时针行走”的副本选择策略。一旦机器再次发生改变（或是单个服务器发生故障），将会违反我们希望的副本放置策略。

回顾 Dynamo 和 Riak Core 的一致性哈希

亚马逊公司于 2007 年发表的 Dynamo 论文影响深远。Riak 采纳了 Dynamo 提出的一致性哈希技术，并且时至今日依然在使用。此外，Cassandra 数据库使用了一种闭源的变体实现，还有其它一些系统也采纳了 Dynamo 的模式。作为一名业界从业者，读论文并思考的感觉很美妙，“这个理念非常好！”，“我可以轻松地编码实现它”。但是，我们同样需要从另一个角度出发，考虑时间和经验并提出疑问“这还是个好主意吗？”

我曾在 Basho Technology 公司维护、支持并扩展了 Riak 的一些子系统。我认为 Riak 曾在 2009 年做了大量有用的工作，并且时至 2018 年看来许多依然是正确的。但其中并不包括 Riak 的一致性哈希。我们在上一节中介绍的局限性，会导致了很多无法避免的实际问题（虽然我们是事后诸葛亮！）。其中一些局限性的根源出在最初的 Dynamo 论文。作为业界，我们现在已具备很多经验，它们来自于 Basho 及其它一些开源分布式系统。自 2007 年以来学术研究领域也得到了十多年的发展，完全改进或取代了 Dynamo 的工作。

Wallaroo Labs 决定为 Wallraoo 寻求一种替代的哈希技术。我们当前使用的方法称为“随机切片”（Random Slicing）技术。下面将做详细介绍。

随机切片：另一种一致性哈希技术

随机切片是 Riak Core 一致性哈希的一种替代技术。随机切片的论文是由 Miranda 等研究人员在 2014 年发表的，论文名是“随机切片：一种用于大规模存储系统的高效、可扩展的数据放置技术”（ Random Slicing: Efficient and Scalable Data Placement for Large-Scale Storage Systems ）。它与 Riak Core 技术的主要区别在于：

1. 可以使用任何能将字符串（以及字节列表和字节数组）映射为整数或浮点数的哈希函数。
2. 不需要将哈希空间可视化地建模为哈希环。副本放置并非取决于查看哈希空间中的近邻分区。
3. 哈希空间可以具有任意数量的分区。
4. 哈希空间中一个分区的规模可以是任意大于零的值。

在我看来，上述差异足以弥补 Riak Core 一致性哈希的所有局限性。下面给出一些示例图，用于介绍随机切片的理念。通过这些示例图，我们将重新查看上文列出的 Riak Core 的主要痛点。

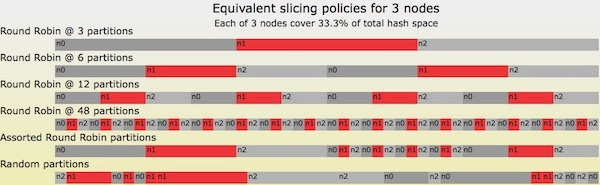
首先给出的示意图（图四）中，显示了一个仅涉及三个节点的随机切片哈希表的所有可能情况。

图四 三个节点映射的六种随机切片策略

在图四显示的所有六种可能情况中，分配给节点、和的哈希空间量分别为 33.3\%$。最上面显示的一种情况是最简单的，即每个节点分配了一个连续的空间。情况 2 到 4 看上去非常类似于 Riak Core 最初的环声明策略，只是没有 Riak Core 的分区个数必须是 2 的指数次幂的局限性。情况 5 也称为“混杂循环分区”（Assorted Round Robin Partitions），事实上它是前面一些情况的组合，包括：情况 2 用于 0%-50% 区间的间隔，情况 4 用于 50%-75% 区间的间隔，情况 3 用于 75%-100% 区间的间隔。最下面显示的是对情况 4 中的间隔做了随机排序。注意，在其中三种情况下，节点分配了相邻的间隔！

随机切片哈希表随时间的变化情况

图四显示的所有情况，都是在某一时刻的有效哈希表随机切片策略。图五给出了一个哈希表的大小随时间变化（沿 Y 轴从上到下）的例子。

图五 一个简单例子，随机切片哈希表的大小从1 个节点调整为4 个节点

图五给出了一种非常不好的情况。我个人并不建议这样使用随机切片。此例说明了随机切片也存在一些并非最优的用法。在本例中，当节点规模依次从一个节点变成两个节点、从两个节点变为三个节点、从三个节点变成四个节点时，哈希空间中变动的键的总数约等于\(50.0 + (16.7 + 33.3) + (8.3 + 16.6 + 25.0) = 150\%\)。这大大超过了最优解决方案产生的数据移动。

图六给出了从一个节点依次增加到四个节点的一种最优转变，该例中进一步采用了重新加权操作。

1. 从单个节点开始，n0。
2. 以权重 weight=1.0 添加节点 n1。
3. 以权重 weight=1.0 添加节点 n2。
4. 以权重 weight=1.0 添加节点 n3。
5. 下面将节点 n3 的权重从 1.0 增大到 1.5。例如，节点 n3 的磁盘容量相比其它节点升级了 50%。

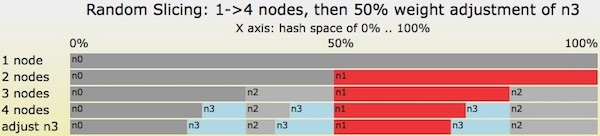
图六 随机切片哈希表的一系列转变，节点数依次从一个添加到四个，之后的权重增大50%

在完成第四步之后，全部四个节点都已经使用同一权重添加，每个节点指派的间隔合计 25%。每步迁移的数据总量以及合计迁移的数据总量都是最优的，即\(50\%+33.3\%+25\%=108.3\%\)。与图五给出的非最优情况相比，图六的步骤避免了大量的数据移动！

在第五步中，节点 n3 的权重从 1.0 增大为 1.5，分配给 n3 的哈希空间总量从 25% 增大到 33.3%。这样，其余三个节点必须放弃一些哈希空间，即每个节点从 25% 收缩到 22.2%。分配的哈希空间比例正是我们所期望的，即\(33.3\%/22.2\%=1.5\)。

最后，我们看一下图七给出的转移情况图。在一开始，在随机切片哈希表中有四个节点。然后我们每次添加三台服务器（表示为图中的一行），共添加四次。最终，随机切片哈希表中将包含 16 个节点。下面，我们使用三种不同的技术查看哈希表，即 Riak Core 一致性哈希、使用最优切片策略的随机切片，以及简单的连续指派策略。

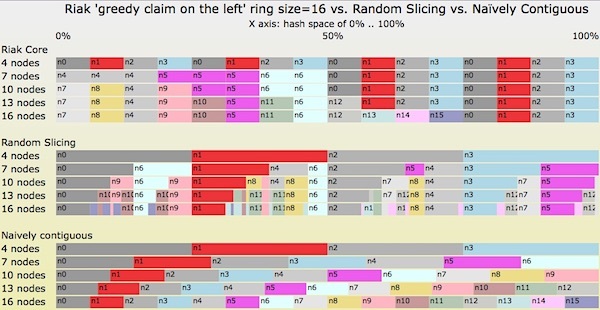
图七 使用三种不同的切片策略，规模依次变为4 个节点、7 个节点、10 个节点、13 个节点到16 个节点。

下面对图七给出几点解释：

1. 最下方的图显示了“简单连续”（Naïvely Contiguous）策略。每次转变都会将哈希空间完全平衡地指派给每个节点，但会导致在每次转变中产生大量无必要的数据移动。
2. 最上方的图显示的是 Riak Core 策略。每次转变中的数据迁移是最优的，但分配给单个节点的哈希空间总量常常是不平衡的
   1. 两种平衡情况：4 个节点和 16 个节点时。所有的节点指派了均等规模的哈希空间，分别为 25% 和 6.25%。
   2. 三种不平衡情况：7 个节点、10 个节点和 13 个节点时。
      1. 对于 7 个节点时，n4 和 n5 指派了三个分区，而其它节点指派了两个分区。不平衡因子为 1.5。
      2. 在 10 个节点和 13 个节点时，n0、n1、n2 和 n3 指派了两个分区，其它节点指派了一个分区，不平衡因子是 2.0。
3. 中间的图显示的是随机切片策略。对于每次转变后的节点的均衡情况，以及每次转变中移动的数据，随机切片策略均是最优的。

随机切片和“Justin Bieber”式超级热键

下面以具有四个节点的哈希表为例，介绍完美的随机切片策略，就是图七所显示的情况。假定我们的 Justin Bieber 式超级热键准确地映射到哈希空间的 6.00000% 处。从图七中可看到，6% 处映射为节点 n0。我们知道 n0 并不能处理 Justin Bieber 式键的全部负载以及所有指派给该节点的其它键。

但是，随机切片允许我们灵活地创建一种非常细微的新分区（例如，范围从 6.00000% 到 6.00001% 的分区），并指派给 n11 节点。这里 n11 是一台 Cray 11 超级计算机，市面上可买到的最快计算节点。这样问题就解决了！

问题或许得到了解决，但是也可能并未解决。现实世界中我们并没有 Cray 11。但是如果使用一种灵活的布置策略，是可以解决 Justin Bieber 问题的。

随机切片和灵活的布置策略

Riak Core 一致性哈希存在一个弱点，目前尚未被随机切片技术解决，那就是布置策略。但是该问题很容易修复，只需要添加一个间接层级！（该方法由 David Wheeler 提出，参见维基百科的“Indirection”词条。

图六（再次给出） 随机切片哈希表的一系列转变，节点从一个添加到四个，之后的权重增大 50%

这里我们重看一下图六。图六一开始，显示了将一个哈希空间间隔映射到单个节点或单个机器的情况。我们在此换种做法，引入一个间接层，转而从哈希空间间隔映射到一种副本安置策略。之后，我们可以定义我们所希望的任一安置策略。例如：

1. 节点 n0 -> 策略 0：使用 Paxos 复制（Paxos Replication）状态机，在节点 82、17 和 22 存储。
2. 节点 n1 -> 策略 1: 使用链复制（Chain Replication）状态机，在节点 77 和 23 上存储。
3. 节点 n2 -> 策略 2：使用 7+2 RS 编码（Reed-Solomon），去除节点 31-39 间的编码条带化。
4. 节点 n3 -> 策略 3：发送数据到位于旧金山的一台彩色打印机。
5. 节点 n11 -> 策略 11：使用一种具有 81 个主备份和二级备份机器的特殊集群。其中，一台主服务器处理 Justin 键值更改问题，其余 80 台只读缓存机器处理由 Justin 粉丝所导致的工作负载。

如何实现随机切片？

下面介绍实现随机切片所需的数据结构、分区策略上的考虑，以及随机切片自身可做的事情。

随机切片实现：数据结构

如果我们当前就需要编写一个随机切片软件库，一种解决问题的方法是只考虑主要的约束。下面列出一些需要考虑的约束：

1. 约束 A：我希望单个范围查询能达到何种性能？即从单个键开始，例如字符串或字节数组，结束时给出一种随机切片分区。
   • 相关问题：我希望随机切片哈希表保留多少个分区？
2. 约束 B：为实现这样的性能，我愿意付出多少内存上的代价？
3. 约束 C：随机切片分区需要存储何种类型的信息？是否需要映射到单个节点名（以字符串、IP 地址或其它形式？），或是映射为一种更通用的放置策略描述？

约束 A 用于选择将字符串或字节数组映射为整数的哈希函数，以及选择用于范围查询的数据结构。对于前者，SHA-1 等加密哈希函数是否足够快？对于后者，是否需要分区表搜索速度 O(1)，或是\(O(log(N))\)即足矣（其中，N 是哈希表的分区数）？

一并考虑约束 A 与约束 B，可以决定使用哪种数据结构进行范围查询。选择的目标是：给定一个整数 V（即所选用的 SHA-1 等标准哈希函数的输出值），那么如何选取随机切片分区 (I,J) 使得\(I\leqslant V< J\)。使用间隔树（interval tree）软件库几乎就能实现上面的工作。同样，使用平衡树（Balance Tree）软件库可以执行“小于或等于”查询，即将所有下限值\(I\)插入树中，然后执行一个小于或等于\(V\)的查询。一些 Trie 树软件库中已经包括此类查询，可为应用在空间与时间的权衡上提供更好的权衡。

如果用户需要自己编写代码，那么一个策略是用排序数组存储所有的下限值\(I\)。在执行小于或等于查询时，可使用二分搜索法查找数组，找到所需的下限值。这正是当前 Wallaroo 使用 Pony 语言实现的方法，：

class val HashPartitions
    let _lower_bounds: Array[U128] = _lower_bounds.create()
    let _lb_to_c: Map[U128, String] = _lb_to_c.create()

• 最初选用的哈希函数是 MD5。MD5 性能可满足 Wallaroo 需求，并输出适用的 128 位值。Pony 原生支持无符号 128 位整数数据和运算。
• 上面给出的数据结构（代码链接）中，使用 U128无符号 128 位整数数组存储每个分区间隔的下限值。
• 使用二分查找法搜索下限值（代码链接）。
• 使用下限整数值作为 Pony Map 类型Map[U128, String]的键。该 Map 的键为一个U128类型的整数，返回一个String类型的值。

最终，我们得到一个String数据类型，它表示了负责输入键的 Wallaroo 工作进程名。如果需要支持更通用的安置策略，可将String类型变更为一个表述所需安置策略的 Pony 对象类型。该方法也可以返回一个整数值，表示安置策略对象数组的索引。

与之相对比，为简化了数据结构，Riak Core 设置了一些局限性，包括固定分区大小、分区数为 2 的指数次幂等。给定一个大小为\(S\)的哈希环，SHA-1 哈希值的前\(\log_{2}(S)\)位用作\(S\)分区描述符数组的索引。

随机切片实现：分区安置（即切片应置于何处？）

随机切片所需的数据结构非常适中。正如在前面图四和图七的例子所示，随机切片的优点主要来自于对哈希分区的巧妙放置和调整大小。那么我们应该使用哪些算法？

我们可以从 Miranda 及其合作者发表的随机切片论文着手。其中可使用一些解决“装箱”问题的算法和策略，尽管标准的装箱算法并不允许更改装箱物体的大小或形状。

从实用的角度看，如果随机切片哈希表的添加操作非常频繁，那么就会创建一些范围非常狭小以至于不能使用底层数据结构表示的分区。在几年前我为Basho 编写的代码中（并未被Riak 使用），底层数据结构使用了介于0.0 到1.0 之间的浮点数。对于一次添加一个节点到哈希表中，如果重复添加操作数十次之后，那么分区范围会变得非常狭小，以至于无法用双精度浮点数变量表示间隔值。

一旦无法对分区做进一步分片时，必须重新分配部分分区，将许多小的分区合并为较大的数个分区。任何这样的重新分配操作都需要移动数据，“没有其它任何理由”，只是为了使分区可以重新做切片。如何选择最小间隔以使得需重新分配的间隔总和最小，同时使创建更大连续分区的优点最大化，这里存在大量值得做进一步研究的优化问题。我们也可以使用另一种方式解决此问题，即升级应用。使用其它一些具有较小最小分区规模的数据结构，解决全部升级的麻烦。任何一种方法都可能适用。

随机切片实现：相关话题

如果我们已经使用了正确的数据结构，并编写了全部的代码实现随机切片哈希表，那么我们是否已经解决了应用中的所有分布式数据问题？虽然我想说是的，但答案是并非如此。还有其它一些事情需要考虑：

1. 随机分片哈希表本身的副本。它可使用某种版本编号方式，也可使用某种保留了历史信息的模式。
2. 在随机切片哈希表发生更改时，如何移动应用的数据。
3. 在应用数据位置发生移动时，如何解决并发访问应用数据的问题。
4. 如何管理上述 1-3 问题中可能出现的所有数据争用问题。

随机切片并不能解决上述任何问题，也不存在一种所谓“分布式应用 + 随机切片 = 大小可调节的分布式新应用”的单一解决方案。这些问题的解决方案是应用特定的。

结论：随机切片是 Riak Core 哈希方法的巨大进步

希望读者能认可我的这一说法，即随机切片方法是一种比 Riak Core 一致性哈希更灵活和更有用的哈希方法。随机切片可提供跨机器的细粒度负载均衡，同时可最小化在随机切片哈希表中添加、删除或重加权计算机时的数据复制。随机切片易于扩展，支持任意的放置策略。通过在随机切片映射中添加范围非常细微的切片，可实现将流量重定向到专用服务器（或放置策略），解决“Justin Bieber“式超级热键的问题。

Wallaroo Labs 将会很快在 Wallaroo 数据处理流水线中使用随机切片技术，实现对处理阶段的管理。Wallaroo 能够在消除不必要的数据迁移的情况下，调整各个参与者的工作负载。这一点非常重要。虽然我们并不需要多种放置策略，但是用户大可放心，无论何时何地一旦有此需要，随机切片将简化这些策略的实现。

线上参考资料

截至 2018 年 8 月，下列 URL 均可正常访问。

1. Bet365，“ Riak Core ”。
2. Decandia 等，“Dynamo：亚马逊公司的高可用键值存储”（ Dynamo: Amazon's Highly Available Key-value Store ”），2007 年。
3. Karger 等，“一致性哈希和随机树：一种用于万维网上热点问题的分布式缓存协议”（ Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web ），1997 年。
4. Metz，Cade，“ How Instagram Solved Its Justin Bieber Problem ”，2015 年。
5. Miranda 等，“随机切片：一种用于大规模存储系统的高效、可扩展数据放置技术”（ Random Slicing: Efficient and Scalable Data Placement for Large-Scale Storage Systems ），2014 年。
6. Sheehy，Justin，“Riak：控制你的数据，而非让数据控制你“（ Riak: Control your data, don't let it control you ），2009 年。
7. Wallaroo Labs，“ Wallaroo ”。
8. Wikipedia，“ Hash Tables ”。
9. Wikipedia，“ Indirection. ”。
10. Gryski，Damian，“一致性哈希：算法上的权衡”（ Consistent Hashing: Algorithmic Tradeoffs ），2018 年。

作者简介

Scott Lystig Fritchie 曾担任 UNIX 系统管理员十多年，从 2000 年开始在 Sendmail 公司转为一名全职编程人员。在 Sendmail 工作期间，有一位同事向他介绍了 Erlang，他的世界从此发生了改变。他曾在 USENIX、Erlang 用户大会和 ACM 上发表过论文，并在 Code BEAM、Erlang Factory 和 Ricon 上发表过演讲。他曾四次担任 ACM Erlang 系列研讨会的联合主席。Scott 目前居住在美国明尼苏达州明尼阿波利斯市，在 Wallaroo Labs 致力于 Pony、Python、Go 和 C 等多语言的分布式系统。

查看英文原文： A Critique of Resizable Hash Tables: Riak Core & Random Slicing