H.266/VVC 标准之仿射运动模型
导言
2020 年 7 月,联合视频专家工作组( JVET )第 19 次会议胜利闭幕,宣告新一代视频编码标准“多功能视频编码 ( H.266/VVC ,后续简称 VVC )”的正式诞生。这距离上一代视频编码标准“高性能视频编码 ( H.265/HEVC )”的问世刚刚过去七年。实际上,近年来随着短视频、在线会议等移动视频应用的爆发式普及,全球的视频信息需求快速增长,业界普遍感受到带宽与存储的巨大压力,极度渴望高性能的视频压缩算法。尽管 2013 年推出的 HEVC 相对于上一代标准“先进视频编码 ( H.264/AVC )”显著提高了压缩性能,但仍无法满足业界日益高涨的需求。针对这种情况,国际标准化组织 ITU-T Video Coding Experts Group ( VCEG ) 与 ISO/IEC Moving Picture Experts Group ( MPEG ) 在 2015 年联合成立了 JVET ,提出了全面超越 HEVC 的战略目标。经过近 3 年的技术积累与酝酿, VVC 标准的制定工作于 2018 年 4 月正式启动。历经 2 年多的艰苦奋战, JVET 的专家们终于在第 19 次会议上完成了 VVC 的标准制定。经过权威评测,编码同质量的视频节目,使用 VVC 相比使用 HEVC 能节省大约一半的带宽。
VVC 使用了大量的新技术,如多叉树块划分技术、历史运动矢量预测技术、亮度色度线性模型预测技术等。本文将重点介绍 VVC 中的仿射运动模型技术。众所周知,标准的文档、参考代码等均为公开资料,相关的学术文献也如汗牛充栋。为了给读者提供更有价值的信息,本文更侧重于相关方法的背景、原理等介绍,不求面面俱到,不拘泥于技术细节,以期读者在短时间内得窥全豹之一斑。
在视频编码的早期研究当中,人们已经发现平动运动模型并不能有效表示转动、缩放等复杂运动。进一步研究发现,仿射( Affine )运动模型能够较好地描述这些复杂运动。从上世纪八十年代开始,学者们研究了整体仿射变换、局部仿射变换等方法,试图在视频编码过程中引入仿射运动模型以提高帧间预测的编码效率。尽管学术界对视频编码中仿射运动模型的研究在近三十年的时间里始终热情不减,但令人遗憾的是,在很长一段时间内仿射运动模型都没能走进代表产业界最新水平的视频编码标准,相关方法始终写在纸面上而不能刻入芯片中。究其原因,大致受困于以下两点。一是仿射运动模型的相关算法复杂度都极高,无论在编码端还是解码端,都超出了同时代实际产品可负担的处理能力。二是相关的研究较为学术化,其设计并没有考虑到算法如何完美地嵌入到现代视频编码标准框架中。现代视频编码标准的整体设计大部分都是基于块划分的混合视频编码框架。如果仿射运动模型无法顺畅地融入这一框架中,也难以被标准采纳。
幸运的是在 HEVC 诞生之后,一系列源于中国学者的创造性研究逐渐破解了上述两大难题,为仿射运动模型走进工业化标准铺平了道路。首先打破僵局的是 Huang 等人 [1] ,他首次提出使用 3 组角点运动矢量来表示一组 6 参数的仿射模型并作为 merge 模式的特别候选的方法。这种方法创造性地利用混合编码框架中存储的运动矢量来表示仿射模型,打开了仿射模型融入混合视频编码框架的大门。 Li 等人 [2] 进一步发展了 [1] 的方法。他将模型参数由 6 个简化为 4 个。更重要的是,他将 [1] 的方法从 Merge 模式推广到了普通 Inter 模式。为了简化编码器,他引入了基于梯度方法的快速运动估计方法以估计仿射模型。为了简化解码器,他将仿射运动模型的运动补偿精度由像素级放大到 4×4 子块级。 [2] 的方法具有里程碑意义,标志着仿射运动模型基本完全克服了上述两大障碍,距离标准化只有一步之遥了。 VVC 启动之后, Zhang 等人 [3] 进一步改进提高了仿射运动模型的编码效率,提出了 4 参数/ 6 参数仿射模型自适应切换、角点运动矢量再预测等方法。 VVC 最终采纳了经过改进的仿射运动模型。经过近四十年的漫长发展,视频编码中的仿射运动模型技术终于凤凰涅槃、修成正果。回首这一历程,我们可以看到一项技术从酝酿、诞生、改进到最终实现工业应用的过程是多么的曲折与艰辛。
从仿射变换到仿射运动补偿
为了更好地理解仿射运动模型技术,我们首先简单介绍一下仿射变换。仿射变换是几何学中的一种常见可逆变换 [4] 。其定义为“如果一个可逆变换前后的共线点组仍为共线点组,则该变换为仿射变换。”从定义可以看出,仿射变换可以保持点的共线性。在几何上可以证明,不共线的点经过仿射变换后仍不共线,平行线经过仿射变换仍为平行线。仿射变换的公式表达为
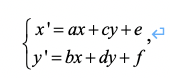
(1)
( x , y ) 和 ( x ’, y’ ) 分别代表变换前后的点坐标。
公式(1)这种形式的仿射变换称为 6 参数仿射变换,是仿射变换的一般形式。可以表出平移、镜像、旋转、缩放、错切五类变换以及它们的组合。
在公式(1)上做限制我们得到
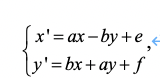
(2)
公式(2)这种形式的仿射变换称为 4 参数仿射变换,是仿射变换的特殊形式。可以表出平移、旋转、缩放三类变换以及它们的组合。可以看出, 4 参数仿射变换的表达能力不及 6 参数仿射变换。但是,在一般地自然视频信号中,平移、旋转、缩放三类运动特征较为常见,镜像与错切较为少见。因此, 4 参数仿射变换用于视频编码领域也有其参数较少的优势。在 VVC 中,这两类仿射变换都可能用到。
当仿射变换用于视频编码中时,即应用所谓的“仿射运动模型”时,我们实际上指的是当前待编码的像素点坐标( x , y )与运动补偿中的参考像素点的坐标( x’ , y’ )存在仿射变换关系。针对公式(1)与公式(2),我们可以很容易得到
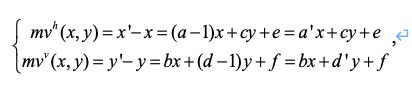
(3)
与
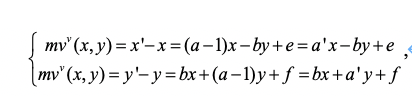
(4)
其中 mv ( x , y ) = ( mvh ( x , y ), mvv ( x , y )) T 代表像素点坐标( x , y )的运动矢量。由于参数可以任意给定,在后文中我们将统一用 a ,d 表示 a’ , d’ 而不会引起误会。
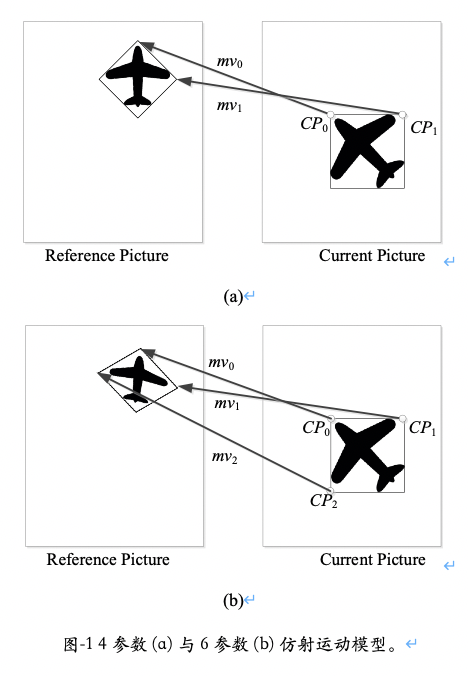
在 VVC 中,对每个编码块我们可以使用一套(单向预测)或者两套(双向预测)仿射模型。在实际中,我们并不会保存或者传输参数 a~f ,而是采用所谓“角点运动矢量导出”的办法,间接保存或者传递这些参数。如图 -1 所示, 4 参数仿射模型可以用左上角的角点运动矢量 mv0 与右上角的角点运动矢量 mv1 来表示; 6 参数仿射模型可以用 mv0 、 mv1 再加左下角的角点运动矢量 mv2 来表示。经过简单公式推导(这里我们省略演算过程),我们可以得到,
针对 4 参数模型:
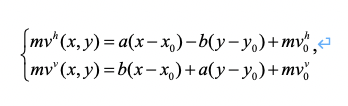
(5)
针对 6 参数模型:
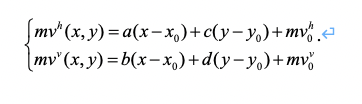
(6)
其中
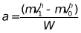
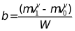
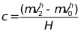
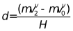
(7)
在上述公式中,我们假设左上角、右上角和左下角三个角点的坐标分别为( x0 , y0 )、( x0 + W , y0 ) 和( x0 + W , y0 + H )。
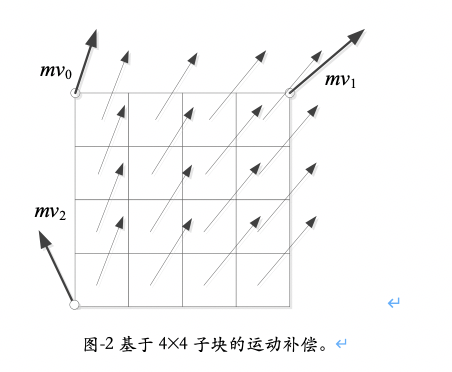
显然,理论上只要给定了一个编码块两个或三个角点运动矢量信息,我们就可以根据上述 4 参数模型或 6 参数模型计算出块内任意位置的运动矢量。但在 VVC 的实现中,为了节省计算量,我们只针对每个 4×4 子块的中心点计算一次运动矢量,整个 4×4 子块中的所有像素将共享这一运动矢量,统一完成运动补偿,如图 -2 所示。这是一种对仿射模型的近似操作,对编码效率造成了一定损失。但是考虑到运算复杂度和硬件带宽等因素,这一近似是必要的。
VVC 中的仿射编码模式
角点运动矢量在 VVC 的仿射运动补偿算法中起到了核心作用。根据角点运动矢量的来源, VVC 的仿射编码模式分为两大类,第一类是仿射 Inter 模式,第二类是仿射 Merge 模式。
采用仿射 Inter 模式时,与普通 Inter 模式类似,运动矢量差值要经过编码传输。不同的是,普通 Inter 模式下,每一个预测方向( List 0/1 )只需要传输一个运动矢量,而仿射 Inter 模式下,需要传输两个( 4 参数仿射模型)或者三个( 6 参数仿射模型)运动矢量来表示两个或三个角点运动矢量(称为角点运动矢量)。编码器可以根据性能优劣选择采用 4 参数仿射模型或者 6 参数仿射模型,之后传输一个标志位来通知解码器选择的结果。解码器据此标志位解码两个或者三个角点运动矢量。采用仿射 Inter 模式时, VVC 支持三种运动矢量的精度,即{ 1/16 , 1/4 , 1}像素精度,编码器将选定的运动矢量的精度信息发送给解码器。
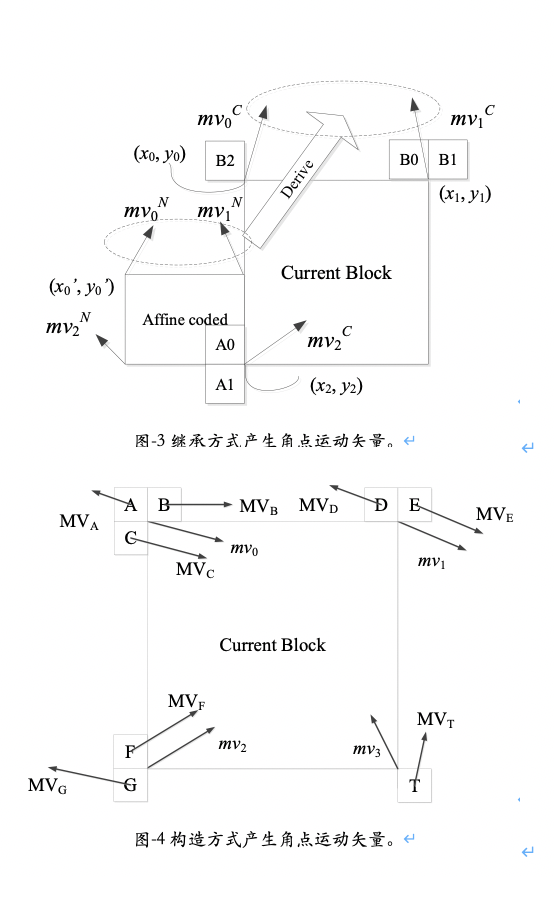
同样与普通 Inter 模式类似,仿射 Inter 模式下将会产生两组预测角点运动矢量候选。预测角点运动矢量的产生方式主要有两种:继承方式(图 -3 )与构造方式(图 -4 )。继承方式利用周边相邻的采用仿射模式编码块(如图 -3 中的 A0 所在的编码块)来推导产生当前编码块的角点运动矢量的预测值。回到公式( 5 )和( 6 ),我们可以看到,实际上公式中并不限制( x , y ) 的范围,这个目标点既可以在块内,也可以在块外。当我们把公式( 5 )或( 6 )套用到 A0 所在的编码块时,如果把目标点坐标置为当前块的左上角(即图 -2 中( x0 , y0 )),我们就可以得到当前编码块左上角的角点运动矢量预测值。类似地也可以得到其他两个角点的角点运动矢量预测值。继承方式得到的角点运动矢量预测准确度较高,在可能的情况下会被优先采用。构造方式则不需要周边相邻的编码块采用仿射模式,而是直接用角点相邻的 4×4 子块所保存的运动矢量来预测角点运动矢量。例如,{ MVA , MVB , MVC }将被用来产生左上角的预测角点运动矢量;{ MVD , MVE } 将被用来产生右上角的预测角点运动矢量;而{ MVF , MVG }将被用来产生左下角的预测角点运动矢量。如果继承方式与构造方式产生的预测角点运动矢量候选不足两个, VVC 还会利用普通 Inter 模式的预测运动矢量去填充各个预测角点运动矢量(实际上,这种情况下相当于预测的仿射模型只有平移运动)以补足预测角点运动矢量的候选。需要注意的是, VVC 中要求产生的预测角点运动矢量与目标角点运动矢量指向相同的参考帧。
有了预测角点运动矢量之后,我们就可以编码角点运动矢量了。左上角的角点运动矢量与普通运动矢量类似,只需要编码其与左上角的预测角点运动矢量的差值( MVD )即可。对于其他两个角点, VVC 中引入了角点运动矢量再预测技术。即:其他两个角点的 MVD 需要用左上角角点的 MVD 再预测一次。用公式表示,在编码端,我们有
mvd0 = mv0 – mvp0;mvd1 = mv1 - mvp1;mvd2 = mv2 – mvp2
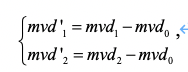
(8)
随后编码端将编码{ mvd0 , mvd’1 } 或者{ mvd0 , mvd’1 , mvd’2 }到解码端。
在解码端,对应的我们有:
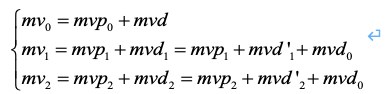
(9)
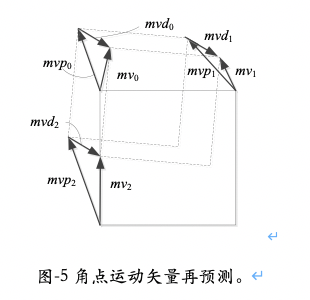
角点运动矢量再预测技术可以提高角点运动矢量的编码效率。如图 -5 展示了一个例子。通常我们认为仿射运动可以分解为平移运动和非平移运动。在 VVC 的仿射模型中,左上角的角点运动矢量 mv0 代表了平移运动,而 mv1 – mv0 与 mv2 – mv0 代表了非平移运动。如果我们分别独立预测平移运动与非平移运动,我们就会得到 mvd0 = mv0 – mvp0而 mvd‘1 = mv1 - mv0 – (mvp1 - mvp0), mvd‘2 = mv2 - mv0 – (mvp2 - mvp0) ,稍加整理,我们就可以得到公式(8)。
仿射 Merge 模式在 VVC 中是作为一种子块 merge 模式出现的。 VVC 中的子块 merge 模式一共有两大类,一类是子块时域运动矢量预测模式,另一类即仿射 Merge 模式。 VVC 中的子块 merge 模式的候选队列第一位为子块时域运动矢量预测模式候选,余下的都是仿射 Merge 模式候选。 VVC 中可以支持多达 5 个仿射 Merge 模式候选。与仿射 Inter 模式类似,仿射 Merge 模式候选的预测角点运动矢量的产生方式主要也是继承方式(图 -3 )与构造方式(图 -4 )两类。与仿射 Inter 模式不同的是,采用仿射 Merge 模式不需要再发送参考帧信息与 MVD 。参考帧信息与运动矢量直接来源于 Merge 模式候选。采用继承方式与构造方式得到的预测角点运动矢量将直接用作仿射 Merge 模式候选的角点运动矢量。另外,仿射 Merge 模式下的构造方式要更为灵活一些,除了左上、右上、左下三个角点的相邻 4×4 子块所保存的运动矢量可以用来估算角点运动矢量之外,右下角的时域预测运动矢量也可以用来预测右下角的角点运动矢量。经过简单换算,右下角的角点运动矢量可以用来推算左上、右上或者左下的角点运动矢量。
仿射运动模型的进一步简化
尽管 [2] 中的方法相对于传统的仿射运动模型编码方式已经有了很大简化,但对于实际应用特别是硬件实现而言,仍显得复杂。针对这一问题, VVC 中对仿射运动模型的运动补偿方式做了进一步简化,主要包括:
针对色域格式 4:2:0 的情况,色度块的子块划分采取 4×4 子块而非 2×2 子块的方式,即一个色度块的子块对应四个亮度块子块。色度块的子块的运动矢量由其对应的左上与右下亮度块子块运动矢量平均得到。这样做可以尽可能减少色度块运动补偿占用的带宽。
VVC 对普通 Inter 块的运动补偿采用 8 抽头亚像素插值滤波器,而对仿射模式的编码块的运动补偿采用 6 抽头亚像素插值滤波器。这是因为普通 Inter 块不会出现 4×4 块的双向预测模式,而仿射模式的编码块会出现 4×4 块的双向预测模式。就平均计算量而言,块尺寸越小,运算量越大。采用 6 抽头亚像素插值滤波器可以尽量减少仿射模式的编码块中亚像素插值的加法和乘法次数。
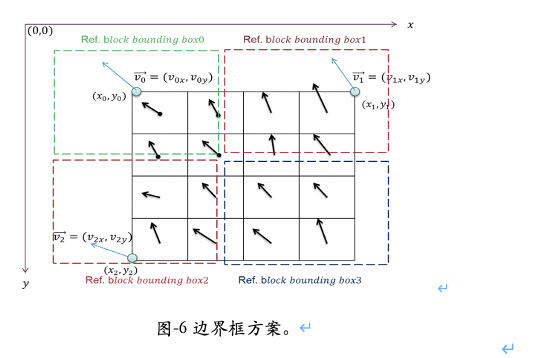
在硬件实现中,运动补偿的块尺寸越小,平均意义上的带宽需求就越高。为了减少 4×4 子块运动补偿带来的高额带宽需求, VVC 采纳了边界框( bounding box )方案,如图 -6 所示。在这一方案中,仿射模式下当前块内部 4 个成田字形的 4×4 子块,他们所对应的参考像素点必须落在同一个边界框内。这个边界框所需要的参考像素仅比一个 8×8 块做运动补偿所需要的参考像素点稍多。这样一来, 4 个成田字形的 4×4 子块的运动补偿的参考像素点可以一次取出,所需的的带宽仅比对一个 8×8 块做运动补偿所需要的带宽稍多。如果不满足上述条件,则当前块退回到普通 Inter 模式,不做仿射运动补偿操作。
仿射运动模型在 VVC 中的性能
JVET 组织在文献 JVET-S0013 中对各个编码工具的编码效率做了官方评测。实验平台为 VTM-9 ,测试环境为 JVET 的官方给出的通用测试环境,包括随机访问( RA )测试,与低延迟 B 帧( LDB )测试。测试方法为关闭待测试的工具,考察 VTM 编码器的性能损失,性能损失越大则表明工具的性能越强。表 1 给出了各个测试序列类别以及总的平均结果。从实验结果可以看出,仿射运动模型在 VVC 中平均可以提供超过 3% 的编码性能增益,对编码器的时间复杂度影响在 20%-30% 之间,对解码器的时间复杂度影响在 3%-8% 左右。对比 JVET-S0013 中所列举的其他编码工具,仿射运动模型可以说是 VVC 中除了灵活块划分结构之外最强有力的编码工具之一。
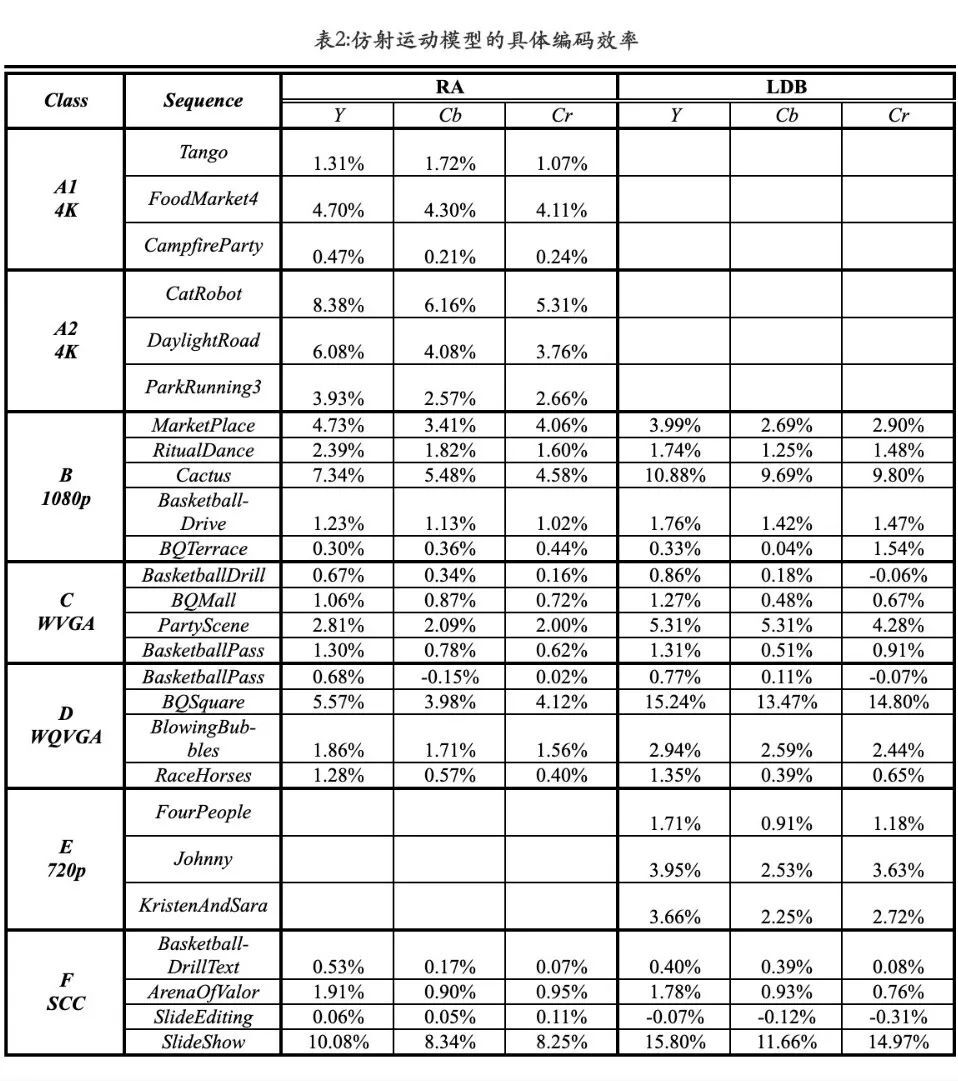
另外,表 2 还列出了各个序列的单独测试结果。我们可以看出,仿射运动模型编码工具的性能对序列的内容有很强的依赖性。对于富含非平移运动的序列,如 Cactus 、 Catrobot 、 BQSquare 、 Slideshow 等,仿射运动模型编码工具可以极大的提高编码效率,最好情况下可以超过 10% 甚至 15% 。但对于不含非平移运动的序列如 Campfire 、 BQTerrace 等,这一工具的效果并不明显。
表 1:仿射运动模型的平均编码效率
后记
视频编码压缩技术,特别是视频编码标准技术,自上世纪 90 年代初的 H.261/MPEG1 到今天一路走来,经过 30 多年的发展,已经成长为极为繁杂庞大的知识体系。以 VVC 编码工具集为代表的新一代编码技术的发展更是日新月异,其精妙程度与行业熟知的传统技术已不可同日而语。本文尝试抛砖引玉,引领有兴趣的读者一览 VVC 中一项非常有特色的新工具——仿射运动模型技术,希望对普及 VVC 的知识有所裨益。如果读者希望进一步了解仿射运动模型技术的理论基础,推荐参考 [5][6] 。由于篇幅有限,一些相关技术,如基于光流的预测修正( PROF )等,本文未作介绍,相关技术细节可参考 [7] 。
参考文献
[1] H. Huang, J. Woods, Y. Zhao, and H. Bai, “Control-point representation and differential coding affine-motion compensation,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 23, no. 10, pp.1651–1660, Oct. 2013.
[2] L. Li, H. Li, D. Liu, Z. Li, H. Yang, S. Lin, H. Chen, and F. Wu, “An Efficient Four-Parameter Affine Motion Model for Video Coding,” IEEE Transactions on Circuits and Systems for Video Technology, Apr. 2017.
[3] K. Zhang, Y. Chen, L. Zhang, W. Chien and M. Karczewicz, “An Improved Framework of Affine Motion Compensation in Video Coding,” IEEE Transactions on Image Processing, vol. 28, no. 3, March 2019.
[4] 尤承业 编著,《解析几何》, 北京大学出版社,2004 年 1 月第一版。
[5] K. Zhang, L. Zhang, H. Liu, J. Xu, Z. Deng and Y. Wang, "Interweaved prediction for video coding", IEEE Transactions on Image Processing, vol. 29, pp. 6422 – 6437, Apr. 2020.
[6] H. Meuel, J. Ostermann, "Analysis of Affine Motion-Compensated Prediction in Video Coding", IEEE Transactions on Image Processing, vol. 29, pp. 7359-7374, June, 2020.
[7] J. Luo, Y. He, “CE2-related: Prediction refinement with optical flow for affine mode,”JVET-N0236, Mar. 2019.





