成为一名顶尖程序员，你需要多少数学知识？

每当我想深入学习一下算法相关的内容时，其中涉及的一些复杂数学知识有时候就会成为“拦路虎”。

我承认自己的数学确实没学好，但也不至于很糟糕。不过，这种“不上不下”的数学水平，完全无法应对业界 Big Tech 公司（亚马逊、苹果、谷歌、Facebook 和微软）的面试，尤其是面试被问到算法的一些问题，比如某个算法的时间和空间复杂度，或者具体的排序和搜索算法之间的比较等。

因此，我要学习所有这些知识点。在搜索和学习过程中，我搜集了几篇有关编程所需的数学知识的文章。

在编程方面，最为知名的数学支持者是史蒂夫·耶格（Steve Yegge）。关于编程所需的数学，我列举了以下内容供你参考：

• 数学笔记
  

• 《Math for Programmers》
  

• 成为一名黑客需要多少数学
  

• 谈数学
  

• 《数学黑客》
  

• 《关于C语言实现的斐波那契数示例》
  

如果你还没读过以上内容，那么你可能会错过我写这篇博客所要表达的意图。按照史蒂夫·萨米特（Steve Summit）、埃里克·雷蒙德（Eric Raymond）以及保罗·格雷厄姆（Paul Graham）的观点，你无需过多地关注数学就可以成为一名出色的程序员或者黑客（此处黑客泛指维基百科中对黑客的定义以及埃里克·雷蒙德（Eric Raymond）对黑客的定义）。

史蒂芬·诺布尔（Steven Noble）认为，程序员应该懂一些数学；埃文·米勒（Evan Miller）似乎在某种程度上也同意这一观点。我本人只是出于热爱而开始踏上编程之路的。

从 2009 年以来，我主要使用 C 语言进行编程，有时候还会用 C++，并且大部分时候是在 Linux 和 UNIX 环境下工作。我对编程充满热情，有时候需要使用多种不同的语言进行编程，因此我必须学习用不同的思维方式工作。编写代码不是很难，但是，使用特定的编程语言并按照一定的范式寻找思路且建立模型，才是最难最耗时的工作。

我在编程道路上的经历告诉我，编程不是数学，而且永远不是。如果你想学习计算机编程，那么去学计算机编程就好了，不需要你去翻阅数学书籍，而是要经常浏览一些编程论坛（比如 comp.lang.c 和 comp.lang.lisp）。关于浏览论坛，你可以使用一个新闻阅读器，比如Pan，订阅来自 GNU 的所有软件信息，并使用 Linux 发行版来处理日常工作，我趋向于使用轻量级版本。如果你想学习计算机编程而学习了大量的数学知识，那么很有可能会迷失在复杂的数学理论当中，并朝着错误的方向前进，最终也不会学到太多的编程知识。

作为一名程序员，我们的任务是编写代码，那我们编写代码的最终目的是什么呢？编写代码的目的当然是解决现实世界中的问题呀！使用代码解决现实世界中的问题，这就是程序员要做的事情。

那数学家是做什么的呢？数学家的任务是使用数学语言来解释自然规律。数学帮我们解决了世界上的许多问题，比如物理学的一个分支量子力学，改变了我们长久以来对原子世界的既有认识，这一进步离不开数据的魔力。数学无处不在，从化学工业到社会问题，我们会用到统计学。日常生活的方方面面，都会看到数学影子。数学不仅可以用来解释自然规律，还能用来解决现实世界中的问题。因为现实世界中的所有变量，都可以用数学语言来描述。

身为一个程序员我并不擅长数学，所以我会试图用自己的直觉、常识、流程图或其他类型的图表来解决工作中遇到的问题。这种状态持续了好几年，并逐渐养成了通过创建模型来解决问题的习惯。建立模型有一个非常明确的目的：对问题及其解决方案要始终保持清晰的思路。可以使用语言符号、流程图或其他形式的图表来创建模型，模型具有明确的假设、规则和条件。向创建好的模型输入数据，经过该模型处理后输出计算结果。模型必须保持清晰和简洁。

数学模型是一种通用的抽象机制，可以应用于特定问题以获取解决方案。几个月前，当我阅读了前面提到的有关数学的文章后，我又读到了埃文·米勒的另一篇名为《Don’t Kill Math》的文章，该文章实际上是为回应布雷特·维克多的《Kill Math》而写的。

这两篇文章有点打击到我。首先，布雷特·维克多一直尝试在做几年以来我做的同样的事情，他在创作方面比我成功。我永远想不出可以适用于任何人的可靠模型，而布雷特已经做到了。是的，我非常高兴，因为我找到了一直在寻找的东西，并且准备跟随布雷特的脚步。但是我从来也没有这样做，这是为什么呢？

我无法提出这样一个可靠的模型是有一定原因的。我一直认为我构建的模型缺点什么东西。无论我做了什么，以及我做了多少工作，我始终感觉缺少一些非常基础的元素。每当我研究 Schrodinger 方程、Maxwell 方程、牛顿定律、开普勒定律、不确定性原理或Shulba-Sutras时，我总是感觉所有这些方程都是完整的，但是我的模型却并不完整。

这两篇文章《Kill Math》和《Dont’ Kill Math》都使我意识到了什么是完整性。这是在文章《Dont’ Kill Math》中提到的一个数学概念。埃文·米勒在本文中提出的问题以及对问题进行简单易懂的解释方式，结束了我对模型的探索。数学是解决问题和解释现象的简洁明了的方法。这些直白了当的特征是数学固有的，就像灵魂是每个生物固有的一样。与不使用数学相比，使用它可以更快更好的解决问题。

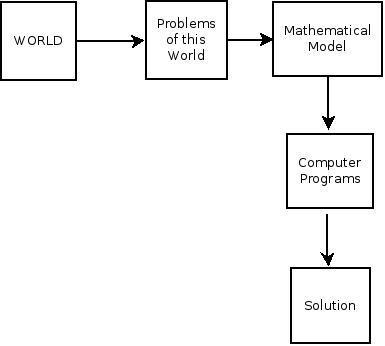
这使我想到了一个非常基础的问题：为什么我会讨厌数学？应该是读书上学的时候，数学的教学方式存在问题。课堂上总是被教导死记硬背数学公式，而不是真正的数学理念。这是学校的错误，是整个教育系统的错误，而不是学生的问题。回到最开始讨论的“成为一名优秀的程序员是否需要数学”这一问题，下图描述的是最开始现实世界解决问题的方式：

然后，数学开始应用，下面这张图描述的是大多数数学家所做的工作：

下图描述的是所有计算机程序员/软件工程师/开发人员所要做的工作：

埃文·米勒提到，你可以在不使用大量数学的情况下成为一名顶尖黑客，我认同他的说法，并且这与其他作者的观点一致。他阐述的重点是数学在解决现实世界中的问题上的作用，即数学在解决现实世界中的问题上简单而又粗暴，而且十分有效。

作为一个程序员，我们的目标是解决问题，但是如果借助数学模型并将其应用到解决方案当中去（如下图所示），那么我们就可以通过一些惊艳的方式来提供更好的解决方案。从而我们的工作生活会变得轻松很多。

总结

你不需要数学就可以成为一名顶尖的程序员，因为在工程上，我们不会直接使用大量的数学理论。如果你想成为程序员，那么就去直接学习编程。计算机编程与数学有很大的不同，作为程序员，你必须更多地专注于如何编写更好的程序，如何使用特定的范式思考（例如，函数、面向对象、泛型、过程、逻辑、声明等），在创建软件的方式上找到更好的方法，你需要了[设计模式，尽管使用 C 语言编程很多年，设计模式仍将会给你的编程思考带来新的认识。所有这些都与数学没有直接联系。你需要优先学习这些编程知识，并且这将会花费好几年的时间才能掌握它们，然后，如果有需要的话，就可以进阶学习数学了。

推荐阅读 Roberrt J. Chassell 的Emacs Lisp编程简介，了解如何创建可自定义、自记录、可扩展的实时文本编辑器。还要推荐学习一下GNU Make Manual，了解为什么需要M4和Autoconf。

数学是理解自然和解决现实世界问题所使用的最广泛的工具。通过学习数学方法，我们可以获取更多解决问题的方法。我本人已经开始研究学习概率学，因为就像史蒂夫·耶格所说的那样，一旦你学会了使用数学工具，你就可以对问题进行初步的分析，判断它是概率问题、微积分问题还是统计问题等。数学与待解决的问题的性质相关，而与程序无关。程序具有解决问题的自身方法和工具，请牢记这一点。

原文链接：

https://lispmachine.wordpress.com/2014/12/05/how-much-math-you-need-for-programming/