DeepMind 提出引导式元学习算法，让元学习器具备自学能力

DeepMind 的一个研究小组近期提出了一种引导式（Bootstrap）的元学习算法，用于解决元优化以及短视的元目标问题，并让学习器具备自学能力。

大部分人类学会学习的过程都是应用过往经验，再学习新任务。然而，将这种能力赋予人工智能时却仍是颇具挑战。自学意味着机器学习的学习器需要学会更新规则，而这件事一般都是由人类根据任务手动调整的。

元学习的目标是为研究如何让学习器学会学习，而自学也是提升人工代理效率的一个很重要的研究领域。自学的方法之一，便是让学习器通过将新的规则应用于已完成的步骤，通过评估新规则的性能来进行学习。

为了让元学习的潜能得到全面的开发，我们需要先解决元优化和短视元目标的问题。针对这两大问题，DeepMind 的一个研究小组提出了一种新的算法，可以让学习器学会自我学习。

元学习器需要先应用规则，并评估其性能才能学会更新的规则。然而，规则的应用一般都会带来过高的计算成本。

先前的研究中有一个假设情况：在 K 个应用中实施更新规则后再进行性能优化，会让学习器在剩余生命周期中的性能得到提升。然而，如果该假设失败，那么元学习器在一定周期内会存在短视偏见。除此之外，在 K 个更新之后再优化学习器的性能还可能会导致其无法计算到学习过程本身。

这类的元优化过程还会造成两种瓶颈情况：

• 一是曲率，元目标被限制在学习器相同类型的几何范围内。

• 二是短视，元目标从根本上被局限在这个评估 K 步骤的平面里，从而无视掉后续的动态学习。

论文中提出的算法包括了两个主要特征来解决这些问题。首先，为减轻学习器短视的情况，算法通过 bootstrap 将动态学习的信息注入目标之中。至于曲率问题，论文是通过计算元目标到引导式目标的最小距离来控制曲率的。可以看出，论文中提出的算法背后的核心思想是，让元学习器通过更少的步骤来匹配未来可能的更新，从而更效率地进行自我学习。

该算法构建元目标有两个步骤：

1. 从学习器的新参数中引导一个目标。在论文中，研究者在多个步骤中，依据元学习器的更新规则或其他的更新规则，不断刷新元学习器的参数，从而生成新的目标。

2. 将学习器的新参数，或者说包含元学习器参数的函数，与目标一同投射到一个匹配空间中，而这个匹配空间简单来说可以是一个欧几里得参数空间。为控制曲率，研究者选择使用另一个（伪）度量空间，举例来说，概率模型中的一个常见选择，KL 散度（Kullback-Leibler divergence）。

引导式元梯度

总体来说，元学习器的目的是最小化到引导式目标的距离。为此，研究团队提出了一种新颖的引导式元梯度（BMG），在不新增反向传播更新步骤的情况下将未来动态学习的信息注入。因此，BMG 可以加快优化的进程，并且就如论文中展示的一样，确保了性能的提升。

研究团队通过大量的实验测试了 BMG 在标准元梯度下的性能。这些实验是通过一个经典的强化学习马尔可夫决策过程（MDP）任务，学习在特定期望下达到最优值的策略进行的。

非稳态网格世界（第5.1节）左：在超过50个随机种子之中，演员-评价者代理下的总回报对比。右：学习的熵值-正则化的时间表。

在Atari ALE[8]的57种游戏中，人类得分标准化。左：2亿帧时，对比BMG与我们实现的STACX*的赛前得分。右：对比公布的基准线与学习得分中位数。阴影部分表示3个随机种子之间的标准偏差。

Atari的消融实验。左：人类标准化得分分解，优化器（SGD，RMS），匹配函数（L2，KL，KL&V），以及引导式步骤（L）。BMG在（SGD，L2，L=1）的情况下与STACX相同。中：不同L下吃豆人关卡返回。右：在57种游戏中关卡返回的分布，按照平均值和标准偏差对每种游戏进行标准化处理。所有结果均为三个独立随机种子，1.9-2亿帧之间观察所得。

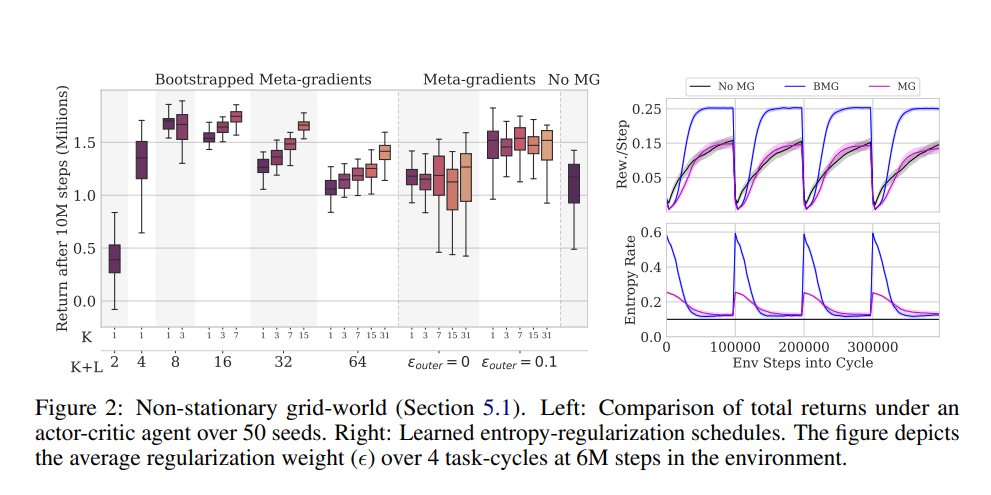
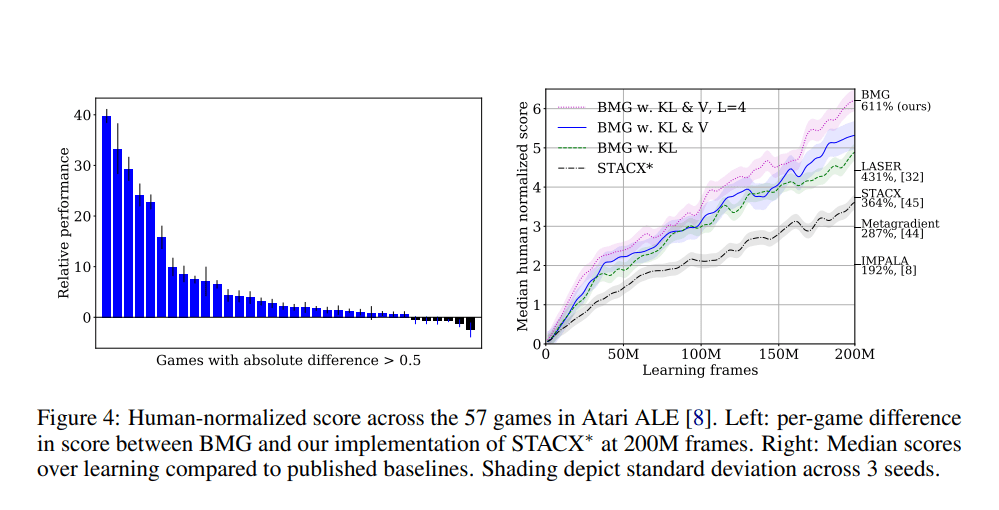
在评估中，BMG 在 Atari ALE 的基准测试中展现了大幅度的性能改进，到达了全新的技术水平。BMG 同样改善了在少数情况下模型诊断元学习（MAML）的表现，为高效元学习探索开拓了新的可能性。

论文地址：https://arxiv.org/abs/2109.04504

原文链接：DeepMind’s Bootstrapped Meta-Learning Enables Meta Learners to Teach Themselves