为什么我的模型表现这么差？

本文最初发表于 Towards Data Science 博客，经原作者 Martin Šiklar 授权，InfoQ 中文站翻译并分享。

你是否经常为你的模型性能而苦恼？你的模型在训练期间表现良好，但当把它应用于新数据时，它却失败了？或者你甚至一开始就在苦苦寻找一个好的模型，因为它似乎没有从你提供的数据中学习到足够的知识？

如果上述任何一种说法适用于你的情况，那么你的模型可能对训练数据过拟合或欠拟合。如果你继续阅读本文，你将学到如何识别这些现象的必要的知识，并获得如何克服这些现象的工具和补救措施，最终提高你的模型性能，这是每一个机器学习工程师的真正目标。

我们将从回归的角度出发，通过 Python 和 scikit-learn 提供的代码示例来研究这个主题。请注意，这篇文章的灵感来自于优秀的书籍《机器学习实用指南》第二版（Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition）这本书是提升机器学习知识的重要资源。

基本知识

作为一个引子，我们先简单地看一下模型的例子，哪些是欠拟合，哪些是过拟合，哪些是表现良好。为此，我们先用一个最简单的回归模型来直观地说明什么是过拟合和欠拟合：线性回归。

欠拟合

假设我们有一些基于二次函数的非线性数据：

import numpy as npn = 100X = 4 * np.random.rand(n, 1) - 2#Quadratic Function: y = ax^2 + bx + cy = 0.6 * X**2 + X + 3 + np.random.rand(n, 1) #adding random noise

很明显，一个简单的线性模型永远无法正确地拟合这个二次数据，但为了演示，我们还是做一下练习吧。

from sklearn.linear_model import LinearRegressionlinear_reg = LinearRegression()linear_reg.fit(X,y)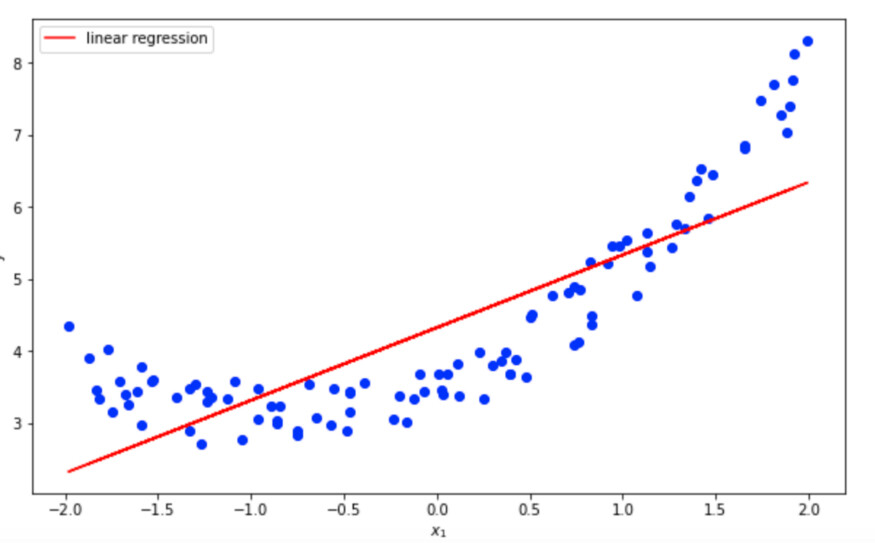

线性模型欠拟合二次数据

你可以看到，线性函数能够检测到数据的总体趋势，但模型完全没有捕捉到非线性（正如预期的那样）。这个模型显然不适合数据，也没有描绘出基本的关系。模型的性能很低。

“完美”拟合

因此，让我们尝试一下多项式回归，它能够捕捉数据中更复杂的关系。实现多项式回归最简单的方法是简单地将每个特征的幂（在我们的例子中是平方，因为我们使用了二次函数）作为新特征，然后应用我们上面使用的线性回归函数。

from sklearn.preprocessing import PolynomialFeatures#add power of two to the datapolynomial_features = PolynomialFeatures(degree = 2, include_bias = False)X_polynomial = polynomial_features.fit_transform(X)#print initial featureprint(X[0])[-1.52521333]#print feature after applying polynomial transformationprint(X_polynomial[0])[-1.52521333  2.32627571]

我们可以看到X_polynomial现在包含了初始特征（-1.52521333）以及它的平方（2.32627571）。如果我们将其输入到线性回归函数中，我们最终会得到一个多项式回归。让我们来看看它与数据的拟合情况。

polynomial_reg.fit(X_polynomial, y)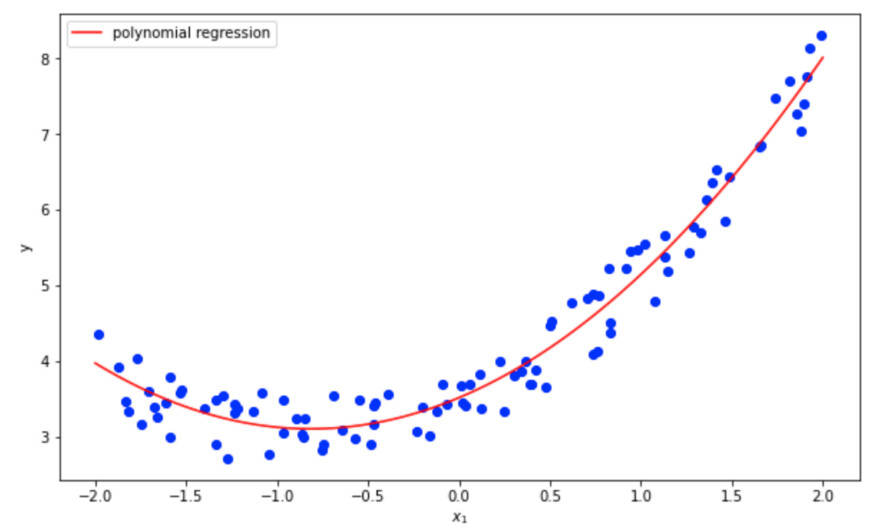

多项式模型拟合二次数据

我们可以检查模型的估计系数，并将其与我们在定义二次函数时使用的系数进行比较。

polynomial_reg.intercept_array([3.51521119])polynomial_reg.coef_array([[1.01029724, 0.61907757]])

模型性能非常好！多项式回归估计的系数与实际系数非常接近，只是由于我们一开始加入了噪声，截距没有被模型很好的捕捉到。

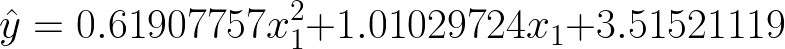
估计模型系数

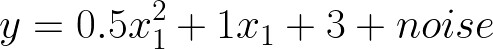
二次函数的实系数

一般的假设是，多项式回归比简单的线性回归更能拟合数据。让我们再看一个例子，用一个更高次的多项式模型来拟合我们的数据。

过拟合

从下面的图片中可以看出，一个更高次（100）多项式模型严重过拟合数据。你可以清楚地看到模型是如何在边缘晃动，以尽可能地拟合训练数据。

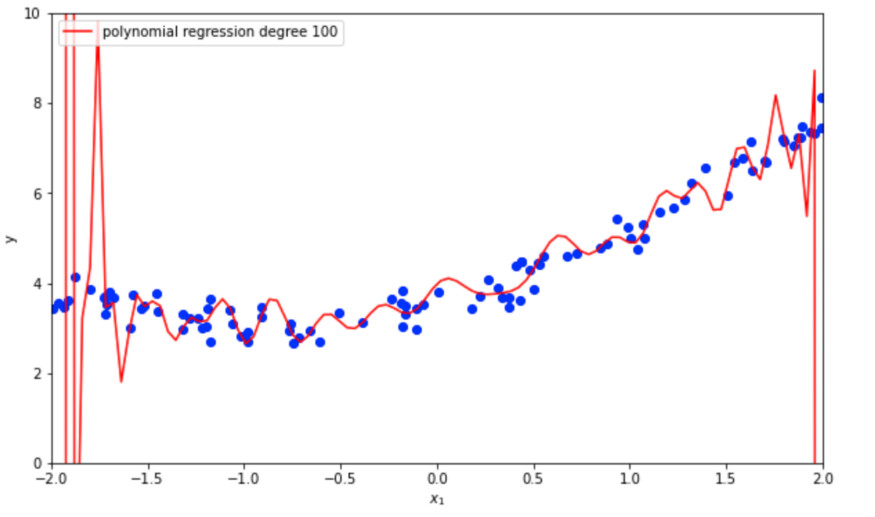
高次多项式模型过拟合二次数据

很明显，从我们的三个例子（线性、2 次多项式和 100 次多项式）中，我们的 2 次多项式模型表现最好，因为基础数据是使用二次函数创建的。

然而，通常情况下，我们并不知道什么函数能以最好的方式代表我们的数据，也不知道什么模型可能是最适合我们的。那么，我们如何找到最佳拟合模型，我们可以遵循哪些标志来判断一个模型的性能呢？

寻找线索

选项 1：分散交叉验证和训练错误

你可能对这个选项很熟悉，因为它是你在文献中最常见的选项之一：交叉验证。这里的总体思路是将训练数据集分割成 k 个较小的子集（fold）。随后，你在其中 k-1 个子集上训练你的模型，并评估模型在剩余子集上的性能。你重复这个过程 k 次，最后得到 k 个评价分数。为了得到总体交叉验证得分，你可以简单地取 k 个分数的平均值。

在 scikit-learn 中，这种方法被称为 K-fold 交叉验证，其基本思想是检查模型在训练集上的表现与交叉验证分数的对比。如果一个模型在训练集上表现良好，但交叉验证分数很低，那么这个模型就是过拟合。如果模型在训练集上的表现很差，而根据交叉验证得分同样很差，则模型为欠拟合。在文献中，正确预测模型从未见过的新数据的能力通常被称为泛化。让我们通过以下例子来说明！

简单线性回归的均方根误差

首先，让我们计算我们的线性回归模型预测在训练数据上的均方根误差（RMSE）。

from sklearn.metrics import mean_squared_errornp.sqrt(mean_squared_error(y, linear_reg.predict(X)))0.7736957615287954

这意味着我们的模型预测与真实数据的平均偏差约为 0.77，这就是我们的训练误差。让我们计算一下我们线性模型的交叉验证分数。在这个例子中，我们将使用 scikit-learn 中的cross_val_score实现，有 10 个 fold。

from sklearn.model_selection import cross_val_scorelin_reg_scores = cross_val_score(linear_reg, X, y, scoring = “neg_mean_squared_error”, cv = 10)

我们得到的是十个输出分数，衡量我们的模型在交叉验证期间的分数。这些模型中的每一个模型都是在 90% 的数据中的不同子集上进行训练，然后用剩下的 10% 的 “看不见的”数据进行评估。总共进行了 10 次。

array([-0.71517651, -0.83664222, -0.631302  , -0.550304  , -0.55877713,-0.56387244, -0.73492102, -0.55389454, -0.49322261, -0.67008695])

为了得到汇总的模型交叉验证误差，我们可以将其与训练过程中的均方根误差进行比较，我们可以简单地取平方根，随后取分数的平均值：

np.mean(np.sqrt(-lin_reg_scores))0.7917563622242139

最后，我们得到了平均交叉验证 RMSE 为 0.79。如果我们将此误差与训练集误差进行比较，我们可以看到大约 0.02 的差异。交叉验证误差高于训练误差是正常的，但 0.02 是好是坏？是高还是低？我们怎么知道呢？再举一个例子，你就知道了！

二次多项式回归的均方根误差

让我们对 2 次多项式回归做同样的练习，看看这些误差与线性模型的误差相比如何。

np.sqrt(mean_squared_error(y,polynomial_reg.predict(X_polynomial)))0.2741445060567453

哇！0.27 远低于我们从线性模型中计算出的 0.77 的 RMSE。我们可以清楚地看到，由于线性模型的训练误差比多项式回归的训练误差要大得多，所以线性模型明显欠拟合数据。现在让我们计算多项式回归的交叉验证误差：

poly_reg_scores = cross_val_score(polynomial_reg, X_polynomial, y, scoring = “neg_mean_squared_error”, cv = 10)np.mean(np.sqrt(-poly_reg_scores))0.28120221324092176

对于多项式模型，我们得到的交叉验证 RMSE 为 0.28，与训练数据的 RMSE 仅相差 0.01。因此，我们可以得出结论：

在我们的例子中，线性回归的 RMSE 远高于多项式回归的 RMSE。此外，我们可以看到，对于线性回归，训练数据和交叉验证之间的 RMSE 差异更大 (0.02>0.01)。这两个标志得出结论，线性回归是欠拟合的数据。

高次多项式回归的均方根误差

最后但并非最不重要的是，让我们看看更高次（100）多项式回归的误差，它在训练数据上得到了惊人的 0.24 的 RMSE，甚至比上面的二次多项式的 RMSE 更好！！

np.sqrt(mean_squared_error(y,higher_polynomial_regression.predict(X_higher_polynomial)))0.24841856155222344

但是交叉验证 RMSE 看起来怎么样呢？是的，它的 RMSE 是 1020471.12，令人瞠目结舌。该模型严重过拟合训练数据（它的 RMSE 是所有模型中最低的），但在看不见的数据上表现糟糕，正如难以置信的高交叉验证 RMSE 所表明的那样。这是一个强过拟合的教科书级别的例子。用机器学习的术语来说，该模型因此具有较差的泛化能力。

higher_poly_reg_scores = cross_val_score(higher_polynomial_regression, X_higher_polynomial, y, scoring = “neg_mean_squared_error”, cv = 10)np.mean(np.sqrt(-higher_poly_reg_scores))1020471.1265272169

解读标志

下面你可以找到一个关于如何解释这些错误的摘要，如果你的模型可能过拟合或欠拟合训练数据，你可以得出结论：

• 高训练误差和更高的交叉验证误差 →欠拟合的标志

• 低训练误差和略高的交叉验证误差 →完美拟合的标志

• 极低的训练误差和极高的交叉验证误差 →过拟合的标志

选项 2：学习曲线

关于如何检测过拟合和欠拟合模型的另一种可能性，是查看它们的学习曲线。学习曲线可视化了模型性能与训练数据大小之间的关系。让我们看看两条学习曲线来解释这个分析背后的基本原理。对于这一部分，我们将使用来自上面的相同数据，这些数据是使用二次函数生成的。

欠拟合学习曲线

首先让我们把训练数据分成一个较小的训练集和验证集。

#split training set into training and validation setX_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=4)train_errors = [] #append training errors for plotval_errors = []  #append validation errors for plot

现在让我们循环遍历新训练集中的观察结果，只从一个观察结果开始。基于此，我们将训练我们的线性回归模型，并使用整个验证集评估其性能。我们将迭代地这样做，并在每一轮的训练集中添加另一个观察，随后是对模型的重新训练，并使用验证集的另一个评估：

#loop over each observation and iteratively compute RMSE for the new training and the entire validation set#in each iteration add one more observation to the training setfor i in range(1, len(X_train)):linear_reg.fit(X_train[:i], y_train[:i])y_train_predicted = linear_reg.predict(X_train[:i])y_val_predicted = linear_reg.predict(X_val)train_errors.append(mean_squared_error(y_train[:i], y_train_predicted))val_errors.append(mean_squared_error(y_val, y_val_predicted))plt.plot(np.sqrt(train_errors), “r-”, linewidth=2, label=”trainining set”)plt.plot(np.sqrt(val_errors), “b-”, linewidth=2, label=”validation set”)plt.legend(loc=”upper right”, fontsize=15)plt.xlabel(“Training / Validation set size”, fontsize=15)plt.ylabel(“Root Mean Square Error”, fontsize=15)

让我们仔细看一下生成的图，先看一下训练集的 RMSE（红线）。最初只有几个实例的时候，训练误差是非常低的，因为线性模型可以很好地拟合一两个实例，但是一旦训练集开始变大，RMSE 就开始非常快速地上升，直到 30 个实例左右达到一个恒定的水平。这时，算法停止了它能学习的东西（记住我们的数据是二次的，而我们的模型是线性的），增加训练数据大小已经没有帮助了。验证集误差（蓝线）最初非常高，因为线性模型只在少数实例上训练。然而，随着每一个新实例加入到训练集中，它迅速变得越来越小，直到很快达到一个比训练集误差略高的水平的平稳状态。这些类型的曲线是数据欠拟合的模型的特征。

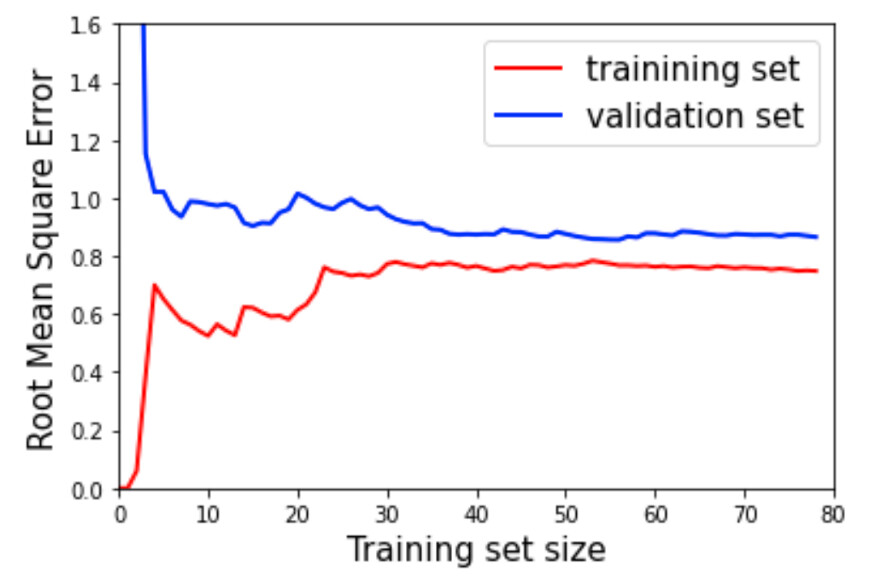
欠拟合模型的学习曲线

过拟合学习曲线

让我们做同样的练习，但用更高的多项式回归代替线性模型。当我们观察新的曲线时，很难真正分辨出它们之间的差别，但我们必须寻找一些细微的迹象，这些迹象告诉我们，我们的模型是过拟合的：这个模型的训练误差一般比之前的线性模型的训练误差低很多。此外，在很长一段时间内，红线和蓝线之间有较大的差距，正如上面已经讨论过的，这是模型过拟合的主要标志之一。一个高的验证误差和一个低的训练误差。

然而，在蓝线的最末端可以看到一个非常有趣的细节：随着训练实例的增多，验证误差开始显著下降，最终非常接近训练误差——最终得到一个更好的模型。

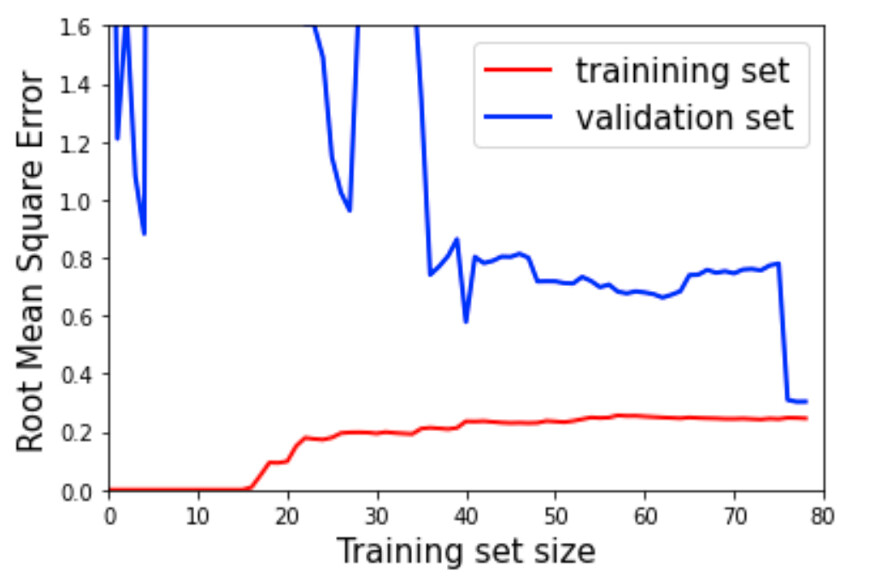
过拟合模型的学习曲线

模型过拟合或欠拟合时，该怎么办？

这也许是最重要的问题，幸运的是，我可以给你留下一套策略，希望能帮助你建立性能更好的模型。

过拟合

• 使用更多的数据！正如我们在上一个学习曲线的例子中所看到的那样，如果你不断向训练数据集添加新的特征，验证误差最终会下降，模型也会停止过拟合。然而，通常情况下，训练数据集是有限的，因此需要一个不同的策略。

• 正则化：换句话说，对模型施加一些约束，降低自由度，对模型施加的约束越多（模型的自由度越少），数据就越难被过拟合。在我们的例子中，这意味着例如降低多项式的次数。在回归方面，你也应该研究一下 Ridge、Lasso 或 Elastic Net Regression，它们对模型权重有不同的约束。

• 然而之后你的训练数据集是有限的，所以你将需要一个不同的策略。

欠拟合

• 使用更多的数据！是的，在这种情况下，更多的数据很可能会在一定程度上提高模型的性能。但是，如果对数据的假设是错误的，你决定使用的分类器无法捕捉到数据的真实性质，那么单纯的增加更多的数据是不会有效果的。

• 增加复杂度：在欠拟合的情况下，对模型施加较少的约束并增加其复杂度，将很有可能得到更好的模型。复杂性的增加可能意味着超越简单的线性模型，利用多项式模型，或者甚至基于树的模型。

当然还有更多的策略来克服这个问题，但是数据量和模型复杂度可以看做是大部分策略中最小的公分母。然而，在你开始切换模型并改变其复杂度之前，你应该首先检查你的模型是否过拟合或欠拟合，这样你就可以开始走向正确的方向。现在，你的背包里应该有必要的工具了吧！

作者介绍：

Martin Šiklar，数据科学家。

原文链接：

https://towardsdatascience.com/why-is-my-model-performing-poorly-b4be05ad3ec6