用算法攻克算法,AI 带来了更多可能性。
瑞典数学家 Lars Garding 曾在其名著《Encounter with Mathematics》中说:“如果不熟悉线性代数的概念,要去学习自然科学,现在看来就和文盲差不多。”作为线性代数中的基本概念之一,矩阵的重要性不言而喻,它可以用来表示线性映射,而矩阵乘法可以用来表示线性映射的复合。
作为一种高效的算法,矩阵乘法在过去几十年间应用性极强,不仅在数学中有大量应用,在应用数学、物理学、工程学等领域也有广泛使用。可以说,矩阵乘法在当代数字世界中产生了巨大的影响,在现代计算中无处不在。
近日,DeepMind 推出的 AI 系统 AlphaTensor 发现了一种新型的矩阵乘法,能够将计算速度提升 20%,这创造了矩阵乘法 50 年最新纪录。该研究成果于 10 月 5 日发表在 Nature 杂志上,并登上了 Nature 封面。这项研究展现了使用机器学习解决数学难题的潜力,在未来,AI 或许还会带来更多的惊喜。
详细算法地址:
https://www.nature.com/articles/s41586-022-05172-4
DeepMind 推出 AlphaTensor,可创造新型矩阵乘法
AlphaTensor 是 DeepMind 研发出的 AI 系统,用于为矩阵乘法等基本任务发现新颖、高效且可证明正确的算法。它解决了数学界 50 年间悬而未决的难题,即找到将两个矩阵相乘的最快方法。
几个世纪以来,数学家认为标准矩阵乘法算法是效率最高的算法。但在 1969 年,德国数学家 Volker Strassen 找到了一种新的 2 x 2 矩阵相乘方法,能够将原本的 8 次乘法减少为 7 次。Volker Strassen 的这一发现震惊了数学界,在此之后,更多研究人员开始探索类似的运算量缩减技巧。

值得一提的是,AlphaTensor 是在 AlphaZero 基础上被开发出来的,后者是应用于象棋、围棋等棋盘游戏中的人工智能体。
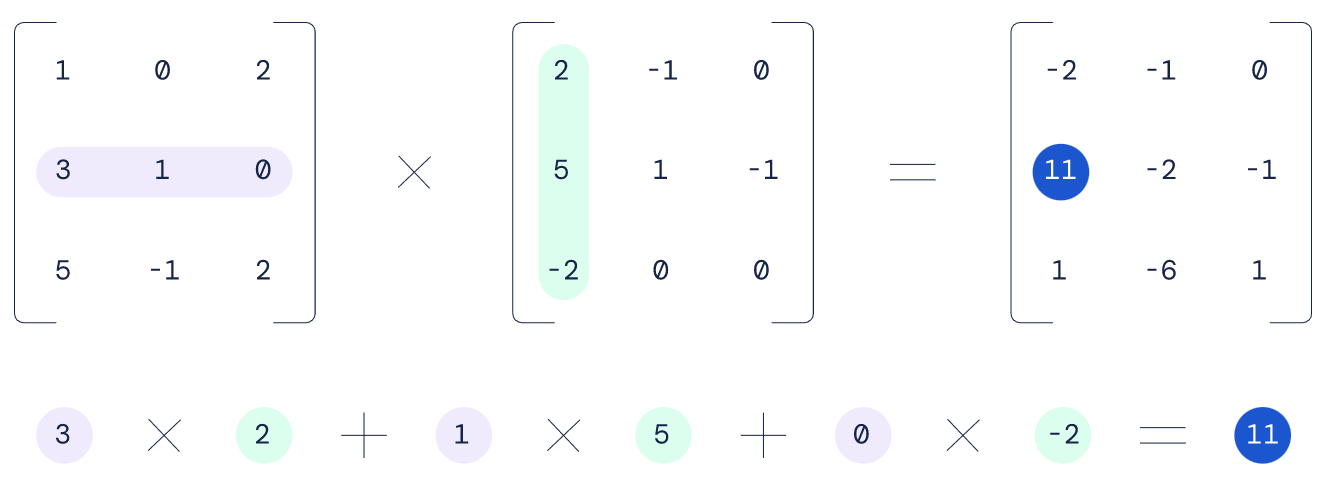
AlphaTensor 的训练过程就是将排列在网格或矩阵中的数字相乘,这些数字可能代表图像中的像素集、天气模型中的空气状况,或者人工神经网络的内部神经元。要将两个矩阵相乘,科学家需要先将各个数字相乘,再用特定方式相加以产生新矩阵。
通过强化学习,AI 智能体能够通过与环境交互学习多步骤目标,例如如何赢下棋盘游戏。如果表现出色,智能体就会得到加强——其内部参数会接受更新,增加后续的游戏成功率。
AlphaTensor 还结合了一种名为树搜索的游戏方法。在这种方法中,AI 会在规划下一步行动的同时,探索各种分支的可能性结果。而在树搜索期间进行路径优先度考量时,它会要求神经网络对每一步的潜在最优行动做出预测。在智能体学习期间,它会使用游戏结果作为反馈以提升神经网络性能,在不断改进树搜索的同时总结出更多可供学习的经验。
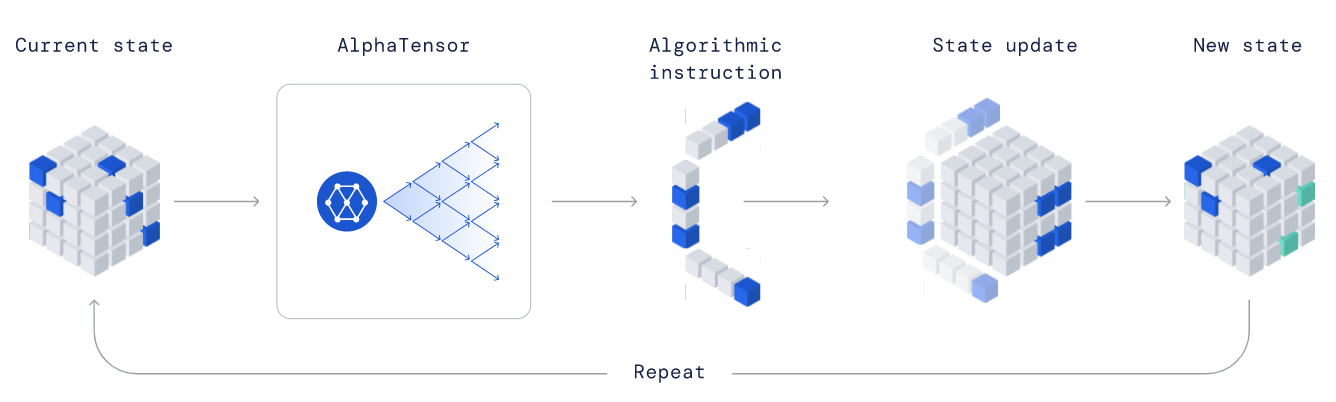
每轮游戏被转化为一场单人拼图,要求智能体正确填写 3D 张量(数字网格)。AlphaTensor 的目标就是用最少的步骤将所有数字归零,而可用的行动已经被预先设定明确。每一步代表一次计算,并在矩阵反转时结合前两个矩阵中的条目以创建出输出矩阵内的一个新条目。这场游戏极为艰难,智能体的每一步行动都可能要从数万亿种行动中做出选择。
论文合著者、DeepMind 计算机科学家 Hussein Fawzi 在发布会上坦言,“算法发现空间的确定非常复杂,找寻在该空间中导航的方法就更难了。”
为了能在训练期间为 AlphaTensor 助力,研究人员还向它展示了一些成功游戏的例子,免得它从零开始胡乱摸索。而且由于行动的顺序并不重要,所以每当它找到一系列成功行动时,研究人员还会将这些行动打乱排序以作为学习示例。
用算法攻克算法,AlphaTensor 实现高效计算
研究人员在高达 5 x 5 的输入矩阵上测试了新系统。在大多数情况下,AlphaTensor 发现的都是 Strassen 和其他数学家之前已经找到的捷径。但令人兴奋的是,它也做出了前人未曾触及的突破。例如,在将 4 x 5 矩阵与 5 x 5 矩阵相乘时,以往的最佳算法需要 80 次单独乘法计算,而 AlphaTensor 发现了只需要 76 次相乘的新算法。
DeepMind 计算机科学家 Pushmeet Kohli 在新闻发布会上表示,“在这场游戏中,它拥有惊人的直觉。AlphaTensor 并没有嵌入任何来自人类的矩阵乘法解题思路。从某种意义上讲,智能体需要从头开始建立自己的知识体系。”
研究人员还创造了一种先将问题拆分成多个较小问题的元算法,借此解决更大的矩阵乘法问题。当 11 x 12 与 12 x 12 矩阵相乘时,这种方法成功将所需的乘法计算次数从 1022 次减少到了 990 次。
AlphaTensor 还能针对特定硬件实现矩阵乘法优化。该团队在两款不同的处理器上进行了智能体训练,不仅减少了计算步骤,也缩短了运行时长。在大多数情况下,与以往的算法相比,该 AI 将矩阵乘法的速度提高了几个百分点。研究人员还发现,有时候一款处理器上最快的算法,在另一处理器上却无法保持优势。
研究人员表示,同样的通用方法也适用于其他类型的数学运算,例如将复杂的波或其他数学对象,分解成更简单的对象。
麻省理工学院计算机科学家 Virginia Vassilevska Williams 表示,“如果能在实践中应用这一成果,将非常令人兴奋。性能的提升将给诸多应用场景带来改善。”维克森林大学的计算机科学家 Gray Ballard 则从中看到了未来人机协作的潜力,“除了用这种方式推动数学探索的边界之外,我还很高兴地看到理论研究人员开始分析这些新发现的算法,其中也许蕴藏着指向其他算法突破的线索。”





