数据库内核杂谈（三十四）- 向量数据库（2）深入浅出聊存储

欢迎阅读新一期的内核杂谈。上一期杂谈关于 vector database 开了个头，介绍了什么是 vector embedding，以及 vector embedding 对于大模型，人工智能的作用。这一期，咱们开始深入学习 vector database 的存储。

相似度（similarity metrics）介绍

在介绍具体的存储格式之前，咱们还需要复习一个前置知识点：similarity metrics。上期聊了用 vector embedding 来描述一个对象。并且介绍了绝大部分应用都是通过计算不同 VE 的相似度（similarity metrics）来完成查询，比如找到非常相似的对象来做推荐。咱们也介绍了一种具体的相似度 metric：cosine similarity（余弦相似度），用来做情感分析。

余弦相似度的数学定义：两个向量之间角度的余弦值。即，它是向量的点积除以它们的长度的乘积。根据计算公式可得出，余弦相似度不依赖于向量的大小，而只依赖于它们的角度。余弦相似度的值总是属于区间[-1, 1]。当两个向量方向相同时（夹角为 0 度），值是 1，两个向量正交（垂直，夹角为 90 度）时是 0，方向相反时值是-1（夹角为 180 度）。下图是计算向量 a 和向量 b 的余弦相似度的公式：

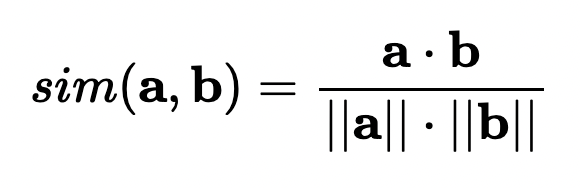
除了余弦相似度，另外两类常见的相似度是 Euclidian distance 和 Manhattan distance。网上和 wiki 上有大量介绍相似度的文章，请允许我 copy-paste 一下。

Euclidian distance（欧几里得距离）:两个向量点在多维空间下的直线距离。下图清晰地展示了什么是 Euclidian distance。

计算公式也很直观：

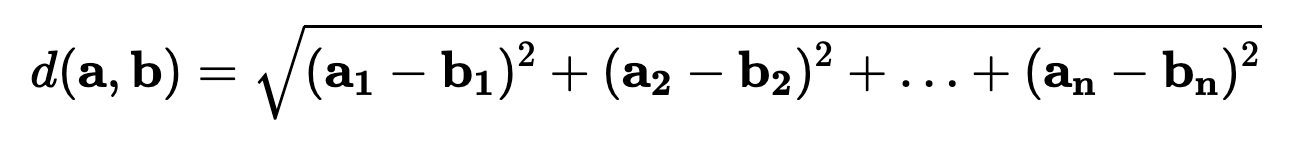
Manhattan distance（曼哈顿距离，又称之为城市区块距离）：对两个向量在每个维度上的差值的绝对值进行求和。下面这张图就能非常直观地展示 Manhattan distance，以及为它被称为 Manhattan distance（因为在曼哈顿，block 都是规整的一个方块一个方块。在曼哈顿，从一个点到另一个点必须走横竖马路）。

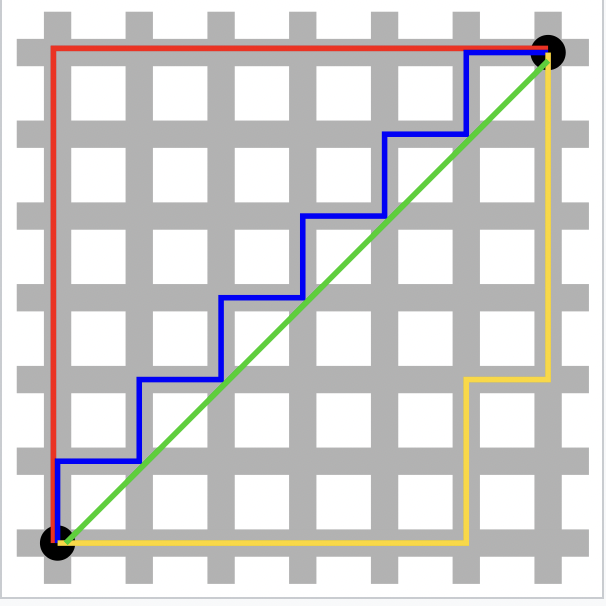
（红黄蓝线都是 Manhanttan distance，而绿线是 euclidian distance）

计算公式如下：

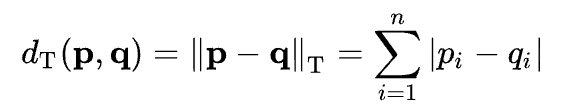
欧几里得距离和曼哈顿距离又是名可夫斯基距离的 L2、L1 的范式的推广（这个不懂也没关系）。

介绍了这些不同的距离定义，那么在 VE 中，应该用哪种距离呢？这又有点玄学了。比如，余弦相似度只比较两个 VE 的角度，和长度无关。对于文本的 VE 比较时，两个文本的长短就不会影响余弦相似度的值。因此，情感分析就更适合用余弦相似度（唠唠叨叨的长篇抱怨和一句“难吃”都能表达出负面情绪）。一般原则就是，使用与训练 VE 的模型相同的相似度 metrics。在不确定的情况下，应该尝试使用各种不同的相似度 metrics 来做计算并且训练模型，以查看是否可以获得更好的结果。

为什么要介绍不同的 similarity metrics 呢？因为，这和我们后面要介绍的存储相关。在向量数据库里，计算不同的 similarity metrics 对应的底层存储数据结构是不同的。向量数据库需要知道业务是如何计算 similarity metrics 来决定如何存储 VE。下图是 Pinecone 数据库创建新 instance 时的配置参数：

万事俱备，终于可以开始介绍具体的存储了。在网上搜索向量数据库的存储，你可能会得到 k-d tree, ball tree, Hierarchical Navigable Small World（HNSW），product quantization，ANNOY 等等劝退的专业名词。内核杂谈尽量遵循深入浅出的方式，来一步一步介绍技术的演进。

Brute-force：linear storage

假设，你在参与一个系统设计面试。面试官的题目就是，你需要设计一个存储方式来存储大量的 vectors；然后，给定一个目标 vector，能够支持某种 similarity metrics 的查询。你会怎么做？

首先，尝试用最暴力，最简单（brute-force）的方式：每个 vector，就作为一个 array 单独存储（我们可以用一些常见的存储 array 的优化方法，如 delta encoding, sparce representation 等，来提升存储每一个 array 的效率）。这被称为 linear storage。

给定一个目标 vector，要查询的相似的 vector 的计算逻辑也非常直观：遍历每一个存储的 vector，和目标 vector 来做 similarity metrics 的计算，返回最接近的值（或者最接近的 k 个值）。算法的时间复杂度是 O(n)。

既然是 brute force 的方法，先来讨论一下这个方法的缺点：计算的时间复杂度太高。每次查询的时间复杂度正比于存储的 vector 的数量。假设有 1 billion 的 vector，每次查询要做 1 个 billion 次的比较（且还是高维向量的计算）。

那这个方法的优点呢？其实还蛮多的。1）算法简单，直观。实现起来也非常容易。2）这个存储方法和 similarity metrics 的计算方式是解耦的。反正每次查询都是拿目标 vector 和存储的 vector 做独立的计算。因此，可以支持不同类型的 similarity metrics 的查询（这和我们后面介绍的一些原生的向量存储格式不同，后者通常只针对某类 similarity metrics）3）和现有的关系型数据库更容易结合，无论是 row-store 还是 columnar-store，都不违和。可以快速地给关系型数据库加入向量数据库的功能。4）结合 GPU 计算资源，SIMD（single-instruction multi-data）指令或者分布式资源，在数据量没有那么海量的情况下，速度也还是可以接受的。

结合上面介绍的优点，虽然 linear storage 是最 brute force 的方法，但这是一个 industry-applicable 的方法。肯定有关系型数据库用这个方法来补完向量数据库的功能。

Tree-based approach: k-d tree

延续刚才的系统设计面试。面试官说，OK！这个方法 work，但缺点就是计算时间复杂度太高。你能提出一个改进方案吗？

要改进时间复杂度，思路就是要提高搜索的效率。Brute force 方法是遍历所有的 vector，提效的思路就是，怎么能减少搜索空间，只进行少量的比较就能查找到相似的 vector 呢。在上面这些铺垫下，我们大致可以想到，二叉树这种数据结构，是不是就能拿来做优化呢。普通的二叉树可以用来存储 scalar 数值（标量），通过构建二叉树来对一个 list 的数据进行排序，在搜索的过程中能够快速查找到相似的数值（时间复杂度是 O(log(n))）。

如何用二叉树来支持向量存储呢，这就是下面要介绍的 k-d tree（k-dimension tree）。k-d tree 是一类特殊的二叉树，用来存储 k 维度的向量，并支持范围搜索和近邻搜索（即，找到相似的 vector）。k-d tree 的构造方式是一个递归过程，通过不断地根据某个 dimension，找到 median point，并将整 search space 一分为二，直到叶节点只有一个向量（当然也可以设置其他的 stop condition，比如当树的深度到达多少为止）。下面是 k-d tree 构造的算法描述：

0）初始化：给定 k 维空间中的一组点。这些点可以代表任何东西，但通常它们是描述某种数据集的特征向量。

1）创建根节点：通过选择一个维度并选择该维度上的中位数点作为根来创建根节点。维度的选择通常是轮流进行的，从第一个维度开始。

2）划分数据：所选择的中位数点将点集分成两半。在所选维度上具有较小值的点进入根的左子节点，具有较大值的点进入右子节点。

3）创建子节点：对于两半中的每一半，沿着下一个维度选择中位数点以创建子节点。再次选择的维度通常是轮流进行的。

4）递归划分：对每个子节点递归重复步骤 2）和 3），将每个节点处的数据划分为两个较小的子集，并创建新的子节点。

5）停止条件：递归继续，直到满足停止条件。停止条件可以是只剩下一个向量。

上面的算法描述非常直观。事实上，实现起来也一点都不复杂。下面是我让 ChatGPT 生成的 Python 代码块（非常直观的递归实现方式）：

class KDTreeNode:    def __init__(self, point, split_dim=None, left=None, right=None):        self.point = point        self.split_dim = split_dim        self.left = left        self.right = right

def build_kdtree(points, depth=0):    n = len(points)
    if n == 0:        return None
    k = len(points[0])  # Dimensionality of the points        # Select the splitting dimension    split_dim = depth % k        # Sort points along the selected dimension    points.sort(key=lambda point: point[split_dim])        # Choose the median point    median = n // 2        # Create the node and recursively build the left and right subtrees    return KDTreeNode(        point=points[median],        split_dim=split_dim,        left=build_kdtree(points[:median], depth + 1),        right=build_kdtree(points[median + 1:], depth + 1)    )

# Example usage:points = [(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)]tree = build_kdtree(points)

给定一个 k-d tree，要搜索相似与目标 vector 的方法类似于在 binary search tree 上做二分查找。在数据结构上还可以做一些优化来快速找到 k 近邻（比如记录这个节点的子节点的数量）。计算复杂度是 O(log(n))。但 k-d tree 只支持 Euclidian distance 和 Manhattan distance 这类距离相似度的查询，并不支持 cosine similarity 这类角度相似度的查询。具体的代码实现，可以留给大家作为课后作业。

k-d tree 的缺点：相比较 linear storage，k-d tree 在搜索的复杂度上提效了。那 k-d tree 有什么缺点呢？1）k-d tree 的构造并不是一棵完全的平衡二叉树（左右子树不平衡，搜索效率不是最优的）。按照上面的算法，虽然每次都是根据某个 dimension 的剩余的点的 median point 来做二分，但这个方式没考虑到其他 dimension 上的数据分布，因此，这个二分是一个 local 的二分法。当向量在某些 dimension 上分布不均匀时，就会导致二分不均匀，进而降低了查询效率。2）如果业务中需要往现有的向量列表里面加入新的向量来搜索，k-d tree 并不能非常高效的支持。k-d tree 可以像普通的二分查找树支持插入新数值一样去插入新向量，但这可能会导致 k-d tree 进一步变得愈发不平衡，从而降低查找效率。并且，k-d tree 很难像自平衡的二分查找树（红黑树或 AVL 树）那样去做自动平衡。原因也是每一层只代表了一个 dimension，很难去做到所有 dimension 的平衡。

总结

本期，咱们介绍了如何存储向量。首先介绍了常见的向量相似度的 metrics：cosine similarity、Euclidian distance 和 Manhattan distance。然后带着大家去思考最简单、最暴力的 brute force 存储方式：linear storage，且分析了它的优缺点。并进一步，引导大家思考，如何提供一个改进 linear storage 缺点的存储方式：k-d tree。下一期的杂谈，会进一步沿着如何改进 k-d tree 的缺点，讨论更多的存储方式。感谢阅读！