最短路径原则,就是将复杂的问题简单化。
达到目标并不是只有一条路,眼前的那条往往也不是最短的一条。所以,解决问题前的第一步,应该是要找实现目标的最短路线。虽然有些人可能会喜欢完成些复杂的算法来获得成就感,但这就是另一个话题了。
要明白,我们是作为实现工具的工人,而不是授命在空中楼阁中研究的学者。
魔术师视角,而不是观众视角
首先是一个比较典型的例子。
那位兄台提出这个问题的时候,问的是碰撞检测。
而且是不规则形状,有凹的也有凸的碰撞检测。判断两个物体是否边缘匹配,可以拼在一起。最后还要在放下时自动检测周围的方块,并自动吸附。必须得说,这个课题真的很困难,倒不是说找不出方法,而是找不出效率可以接受的方法。优化的办法应该是有的,但是我不会,因为这个还得吸附啊,我哪知道哪边才是边。但后来我觉得不对劲,就问了下他实际要做的东西。
才知道这家伙原来是做——拼图。
所谓拼图,就是一个图片被拆成各种不规则形状然后打乱,然后让玩家重拼起来,需求就是这样。好吧,既然是这样,那么记下这些碎片的原始位置,然后判断你手上的碎片目前坐标是否接近这个位置不就好了。
电脑没有必要使用人的思维,设计者没必要使用玩家的思维。完全模拟,并不是最好的方案。
首先考虑简单的近似实现
老外的东西总是能有惊喜。老外的思路常常都很单纯,过度设计的情况很少见。不管怎么说,他们的经验还是要丰富一些的。虽然一个需求怎么都能实现,但细微之处的积累依然会产生大的变化。这次嘛,是关于一个同事在玩的 SNS 游戏,它里面捡钱会曲线飞到表示钱的数字上这个效果挺别致的。
国内的情况,连做个直线飞就已经多余了,更不要说曲线了。但曲线的效果的确比直线生动很多。然后我就在仔细观察它的轨迹,考虑它是怎么实现的,想做一个类准备着以后来用。一般的想法,是用二次贝尔法曲线公式计算出运动轨迹,虽然需要一定的数学公式但曾经做过应该不成问题,而且 TweenMax 也提供了这个功能,但既然是曲线就有曲率的问题,而参考的效果并不是固定的 1/4 圆,况且这种做法有些太小题大作了。然后就是考虑物理移动,但原效果看起来使用了圆缓冲,越接近目标越慢,而且是平行 y 轴结束,这个用物理模拟会比较困难……
最后我脑子突然灵光了。让 X 轴方向用匀速移动,Y 轴方向减速圆缓冲移动,看起来貌似就是画面里的样子……
也就是代码:
TweenLite.to(target,{x:tx });
TweenLite.to(target,{y:ty,ease:Circ.easeIn });
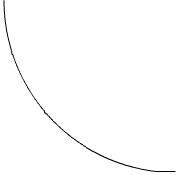
其结果就是弧线,和原品一模一样的。很显然,这还要做类会很无聊。
即使有复杂的解决方案,也应该考虑是否有更简单的方案。复杂的方案只是适用范围更广泛而已,但既然有“这么简单”的,何必去费那个事呢。
到现在还不知道 TweenLite 是什么的参见以下地址: http://www.greensock.com/tweenlite/
“根据需求选择技术”VS“将适用的技术用于需求”
说到这里,正好提下四叉树的问题。四叉树的确是一个很经典的解决屏幕物品筛选遍历的方案。具体是怎么做的可以参考网上的其它资料,可惜原理讲起来有些拗口,实现也比较恶心,所以目前并没有被广泛使用。
但是这东西不就是筛选屏幕内物品用的么?因为有两个坐标,可以将物品按坐标归类。这里我们又犯了“将适用的技术用于需求”而不是“根据需求选择技术”的错误。四叉树的确可以用来快速筛选屏幕内的物品,但并不是说筛选屏幕内的物品就只能用四叉树。要知道四叉树可以处理任意缩放屏幕,以及无限大的坐标系内的快速筛选,但我们实际上需要的就是几十屏以内固定屏幕大小内的筛选。
实际上,有个很好理解的代替方案。我们可以创建一个二维数据,诸如地图是 10000*10000 的,屏幕大小是 1000*1000,我们就创建一个 20*20 的二维数组,然后将坐标范围在 (0-500,0-500) 的物品存在数组的 (0,0) 项内,将 (500-1000,0-500) 存在数组的 (1,0) 项内,将 (1000-1500,0-500) 存在数组的 (2,0) 项内,将 (1000-1500,500-1000) 存在数组的 (2,1) 项内,将 (1000-1500,1000-1500) 存在数组的 (2,2) 项内……然后将地图里的所有物品按这个方式保存在二维数组里,物品移动时则更新数组。
到时候要取屏幕范围,就以屏幕中心坐标开始,除以 500 获得一个区块的坐标,然后取他周围的九个区块,这些区块内保持的物品实例肯定覆盖了整个屏幕。虽然会多出一些屏幕外的物品,但这点多余消耗是可以接受的。
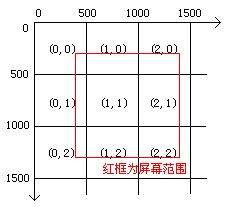
这和使用四叉树的结果是相同的,都可以快速定位屏幕内物品,做到游戏中存在大量物体,但只要不同时出现在同屏,就不会耗费过多遍历性能的目的。
关于四叉树遍历可以参考衰人的日志:( http://wxsr.blogbus.com/logs/60788934.html )
特殊情况应当使用特殊处理
子弹会穿墙,这是个经典问题。
现实的子弹是线性移动的,电脑中的却不是。子弹的移动一定是间隔进行的,而子弹的速度很快,体积小,墙壁薄的时候,就有几率正好跨过去导致碰撞检测失效。这其实是满经典的问题,像以前玩沙罗曼蛇,全部吃加速吃到一定程度就可以玩穿墙了,毕竟碰撞检测是一个高消耗的操作,能简化就简化,尤其是在飞行射击游戏出现大量子弹的情况下,采用复杂的判断逻辑实在不合算。
需要注意到,在设定好的环境里,子弹穿墙的几率实际上是很低的。这种游戏子弹是要能看到并躲避的,速度就不能太快。就算那子弹的确比较快,只要你墙壁别薄到看不到,一般也是穿不过去的。如果这两个条件都满足,我只能认为你游戏设计稍微有点问题。
好吧,说到解决方案,最彻底的当然是计算移动轨迹并判断是否和障碍物的边缘相交,这并不算困难,但是性能消耗会翻倍,仅仅是为了特殊状况,确实有这样做必要么?
如果游戏里所有子弹都是会穿墙的速度,这游戏基本就不用玩了。所以,能穿墙的只会是某些特定的高速弹。仅仅为了这个而使其它正常速度的子弹的碰撞判断降低性能,这个做法并不妥当,那实际上可以怎么做呢?
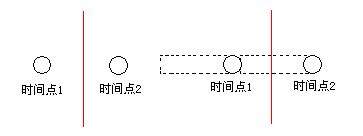
你只要将你的特定子弹尾部延长就可以,就是修改子弹素材,在尾部添加一条透明的尾巴并参与碰撞。虽然看起来是点,却是线。这样要想穿墙难度就高很多了。而这个延长部分是感受不出来的,因为它是高速弹,来无踪去无影,不可能抓得到尾巴。
步骤的对调可能大幅简化逻辑
当时是心血来潮想做个爆炸效果。就是那种哐啷一声一块玻璃被切成一片片散落的样子。例子可以参考 FFX 的战斗切换,以及 DMC3 关卡结束的切换动画。
这个效果其它部分都很简单,难点在于切割。碎裂的方式是随机的,首先是创建一堆随机的点,然后三点组合成三角形,问题就在于如何组合。三角形当然是不能交叠的,所以你需要将接近的点组合成三角形,而且保证它们不会叠在一起,问题就转变为“什么样的点才叫接近的点”。这个算法倒是在哪看到过,不过我不记得就是了……
查也查不到,所以我就找个了近似方案代替。这里关键的问题在于点的随机性,只要点不是随机的,组合三角形就可以用 ((0,0),(0,1),(1,0)),((0,1),(1,0),(1,1)) 这个约定的组合,然后保证随机的时候不会交叉就可以了。
首先是创建出不考虑随机的状况,差不多就像下面这样,平均切成矩形,矩形再分成两个三角形。此时顶点到三角形的组合规律是固定的。
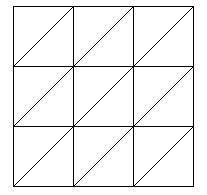
把这个作为原始状态,再调整顶点的位置,可以看到,即使将各个顶点分开移动,每个顶点只要还在矩形范围内活动,三角形就不会交叠。
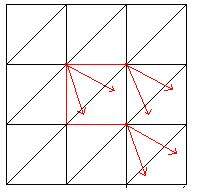
其结果就是这样,虽然不是完全随机,但基本可以符合要求。
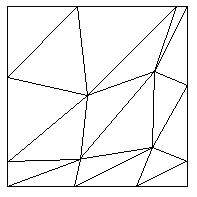
除去必须在边缘上的点之外,中间自由活动的点的坐标可以这样简单地求出来
x = dx * (i + Math.random())
y = dy * (j + Math.random())
其中 dx,dy 是分割的小矩形的长宽,i,j 是顶点的 x,y 序号。
换个思路,就有新的方向。先创建顶点再组合三角形,和创建三角形再调整顶点,难易程度就会完全不同。




